5.6 Substitution Method
Integration (antidifferentiation) is generally more difficult than differentiation. There are no sure-fire methods, and many antiderivatives cannot be expressed in terms of elementary functions. However, there are a few important general techniques. One such technique is the Substitution Method, which uses the Chain Rule “in reverse.”
The term “integration” is used in two ways. It refers to:
- The process of finding areas or differences of areas (computing a definite integral), and also
- The process of finding an antiderivative (evaluating an indefinite integral).
Consider the integral \(\int 2x\cos(x^2)\, \mathrm{d}x\). We can evaluate it if we remember the Chain Rule calculation \[ \dfrac{d}{dx} \sin(x^2) = 2x\cos(x^2) \] This tells us that \(\sin(x^{2})\) is an antiderivative of \(2x\cos(x^{2})\), and therefore, \[ \int\underbrace{\phantom{(}2x\phantom{)}}_{\substack{\text{Derivative of}\\\text{inside function}}} \cos\underbrace{(x^2)}_{\substack{\text{Inside}\\\text{function}}}\, \mathrm{d}x = \sin(x^2) + C \] A similar Chain Rule calculation shows that \[ \int\underbrace{(1+3x^2)}_{\substack{\text{Derivative of}\\\text{inside function}}} \cos\underbrace{(x+x^3)}_{\substack{\text{Inside}\\\text{function}}}\, \mathrm{d}x = \sin(x+x^3) + C \] In both cases, the integrand is the product of a composite function and the derivative of the inside function. The Chain Rule does not help if the derivative of the inside function is missing. For instance, we cannot use the Chain Rule to compute \(\int \cos(x+x^3)\, \mathrm{d}x\) because the factor \((1 + 3x^{2})\) does not appear.
Question 5.20 Substitution Progress Check Question 1
Find the antiderivative of \(\cos x e^{\sin x} \)
| A. |
| B. |
| C. |
| D. |
 REMINDER
A “composite function” is a function of the form \(f(g(x))\). For convenience, we call \(g(x)\) the inside function and \(f(u)\) the outside function.
REMINDER
A “composite function” is a function of the form \(f(g(x))\). For convenience, we call \(g(x)\) the inside function and \(f(u)\) the outside function.
329
In general, if \(F'(u) = f(u)\), then by the Chain Rule, \[ \dfrac{d}{dx} F(u(x)) = F'(u(x))u'(x) = f(u(x)) u'(x) \] This translates into the following integration formula:
THEOREM 1 The Substitution Method
If \(F'(x) = f(x)\), then \[ \boxed{\bbox[#FAF8ED,5pt]{\displaystyle \int f(u(x)) u'(x)\, \mathrm{d}x = F(u(x)) + C}} \]
Substitution Using Differentials
Before proceeding to the examples, we discuss the procedure for carrying out substitution using differentials. Differentials are symbols such as \(\mathrm{d}u\) or \(\mathrm{d}x\) that occur in the Leibniz notations \(\mathrm{d}u\over\mathrm{d}x\) and \(\int f(x)\, \mathrm{d}x\). In our calculations, we shall manipulate them as though they are related by an equation in which the \(\mathrm{d}x\) “cancels”: \[ \mathrm{d}u = \frac{\mathrm{d}u}{\mathrm{d}x}\mathrm{d}x \] Equivalently, \(\mathrm{d}u\) and \(\mathrm{d}x\) are related by \[ \boxed{\bbox[#FAF8ED,5pt]{\displaystyle \mathrm{d}u = u'(x)\, \mathrm{d}x}}\tag{1} \] For example, \[ \begin{array}{lcl} \text{If }u=x^2, & \text{then} & \mathrm{d}u=2x\, \mathrm{d}x\\ \text{If }u=\cos(x^3) & \text{then} & \mathrm{d}u=-3x^2\sin(x^3)\, \mathrm{d}x \end{array} \] Now when the integrand has the form \(f(u(x))\) \(u'(x)\), we can use Eq. (1) to rewrite the entire integral (including the \(\mathrm{d}x\) term) in terms of \(u\) and its differential \(\mathrm{d}u\): \[ \boxed{\bbox[#FAF8ED,5pt]{\displaystyle \int \underbrace{f(u(x))}_{f(u)}\underbrace{u'(x)\, \mathrm{d}x}_{\mathrm{d}u} = \int f(u)\, \mathrm{d}u}} \]
The symbolic calculus of substitution using differentials was invented by Leibniz and is considered one of his most important achievements. It reduces the otherwise complicated process of transforming integrals to a convenient set of rules.
This equation is called the Change of Variables Formula. It transforms an integral in the variable \(x\) into a (hopefully simpler) integral in the new variable \(u\).
EXAMPLE 1
Evaluate \(\displaystyle \int 3x^2\sin(x^3)\, \mathrm{d}x\).
Solution The integrand contains the composite function \(sin(x^{3})\), so we set \(u = x^{3}\). The differential \(\mathrm{d}u = 3x^{2}\, \mathrm{d}x\) also appears, so we can carry out the substitution: \[ \int 3x^2\sin(x^3)\, \mathrm{d}x = \int \underbrace{\sin(x^3)}_{\sin(u)}\underbrace{3x^2\, \mathrm{d}x}_{\mathrm{d}u} = \int \sin u\, \mathrm{d}u \]
In substitution, the key step is to choose the appropriate inside function \(u\).
Now evaluate the integral in the \(u\)-variable and replace \(u\) by \(x^{3}\) in the answer: \[ \int 3x^2\sin(x^3)\, \mathrm{d}x =\int \sin u\, \mathrm{d}u = -\cos u +C = -\cos(x^3) + C \]
330
Let’s check our answer by differentiating: \[ \dfrac{d}{dx} (-\cos(x^3)) = \sin(x^3)\dfrac{d}{dx}x^3 = 3x^2 \sin(x^3) \]
Question 5.21 Substitution Progress Check Question 2
Use the substitution \(u = \sin x\) to rewrite the integral \(\int \cos x e^{\sin x} \ dx\)
| A. |
| B. |
| C. |
| D. |
EXAMPLE 2 Multiplying \(\mathrm{d}u\) by a Constant
Evaluate \(\displaystyle \int x(x^2+9)^5 \mathrm{d}x\).
Solution We let \(u = x^{2} + 9\) because the composite \(u^{5} = (x^{2} + 9)^{5}\) appears in the integrand. The differential \(\mathrm{d}u = 2x\, \mathrm{d}x\) does not appear as is, but we can multiply by \(\tfrac12\) to obtain \[ \dfrac12\, \mathrm{d}u = x\, \mathrm{d}x \implies \dfrac12u^5\, \mathrm{d}u = x(x^2 + 9)^5\, \mathrm{d}x \] Now we can apply substitution: \[ \int x(x^2 + 9)^5\, \mathrm{d}x = \int \overbrace{(x^2+9)^5}^{u^5} \overbrace{x\, \mathrm{d}x}^{\tfrac12\, \mathrm{d}u} = \dfrac12 \int u^5\, \mathrm{d}u = \dfrac1{12}u^6 + C \] Finally, we express the answer in terms of \(x\) by substituting \(u = x^{2} + 9\): \[ \int x(x^2 + 9)^5\, \mathrm{d}x = \dfrac1{12}u^6 + C = \dfrac1{12}(x^2+9)^6 + C \]
Substitution Method:
- Choose \(u\) and compute \(\mathrm{d}u\).
- Rewrite the integral in terms of \(u\) and \(\mathrm{d}u\), and evaluate.
- Express the final answer in terms of \(x\).
EXAMPLE 3
Evaluate \(\displaystyle \int \dfrac{(x^2 + 2x)\, \mathrm{d}x}{(x^3 + 3x^2 + 12)^6}\).
Solution The appearance of \((x^{3} + 3x^{2} + 12)^{-6}\) in the integrand suggests that we try \(u = x^{3} + 3x^{2} + 12\). With this choice, \[ \mathrm{d}u = (3x^2 + 6x)\, \mathrm{d}x = 3 (x^2 + 2x)\, \mathrm{d}x \implies \dfrac13 \mathrm{d}u = (x^2+2x)\, \mathrm{d}x \] \[ \begin{aligned} \int \dfrac{(x^2 + 2x)\, \mathrm{d}x}{(x^3 + 3x^2 + 12)^6} & = \int \overbrace{(x^3 + 3x^2 + 12)^{-6}}^{u^{-6}} \overbrace{(x^2 + 2x)\, \mathrm{d}x}^{\tfrac13\, \mathrm{d}u}\\ & =\dfrac13 \int u^{-6}\, \mathrm{d}u = \left(\dfrac13\right)\left(\dfrac{u^{-5}}{-5}\right) + C \\ & = - \dfrac1{15}(x^3 + 3x^2 + 12)^{-5} + C \end{aligned} \]
CONCEPTUAL INSIGHT
An integration method that works for a given function may fail if we change the function even slightly. In the previous example, if we replace 2 by 2.1 and consider instead \(\displaystyle \int\dfrac{(x^2 + 2.1x)\, \mathrm{d}x}{(x^3 + 3x^2 + 12)^6}\), the Substitution Method does not work. The problem is that \((x^{2} + 2.1x)\, \mathrm{d}x\) is not a multiple of \(\mathrm{d}u = (3x^{2} + 6x)\, \mathrm{d}x\).
EXAMPLE 4
Evaluate \(\displaystyle\int \sin(7\theta+5)\, \mathrm{d}\theta\).
Solution Let \(u = 7 \theta + 5\). Then \(\mathrm{d}u = 7\, \mathrm{d}\theta\) and \(\tfrac17\, \mathrm{d}u=\mathrm{d}\theta\). We obtain \[ \sin(7\theta+5)\, \mathrm{d}\theta = \dfrac17 \int \sin u\, \mathrm{d}u = -\dfrac17 \cos u + C = -\dfrac17\cos(7\theta + 5) + C \]
Question 5.22 Substitution Progress Check Question 3
Evaluate \(\displaystyle \int \sqrt[5]{1+7x} \ dx\)
| A. |
| B. |
| C. |
| D. |
331
EXAMPLE 5
Evaluate \(\displaystyle \int e^{-9t}\, \mathrm{d}t\).
Solution Use the substitution \(u = -9t\), \(\mathrm{d}u = -9\, \mathrm{d}t\): \[ \int e^{-9t}\, \mathrm{d}t = \int e^{u}\left(-\dfrac19\, \mathrm{d}u\right) = -\dfrac19\int e^u\, \mathrm{d}u = -\dfrac19 e^u + C = -\dfrac19 e^{-9t} + C \]
EXAMPLE 6
Evaluate \(\displaystyle \int \tan\theta\, \mathrm{d}\theta\).
Solution In this case, the idea is to write \(\displaystyle \tan\theta\, \mathrm{d}\theta = \dfrac{\sin\theta\, \mathrm{d}\theta}{\cos\theta}\) and to note that if \(u = \cos\theta\). Then \(\mathrm{d}u = -\sin\theta\, \mathrm{d}\theta\) and \[ \int \tan\theta\, \mathrm{d}\theta = \int \dfrac{\sin\theta\, \mathrm{d}\theta}{\cos\theta} = - \int \dfrac{\mathrm{d}u}{u} = -\ln|u| + C = - \ln|\cos(\theta)| + C \] Now recall that \(-\ln u = \ln\tfrac 1u\). Thus, \(-\ln|\cos(\theta)| = \ln\tfrac1{|\cos(\theta)|}\) and we obtain \[ \int \tan\theta\, \mathrm{d}\theta =\ln\lvert\dfrac{1}{\cos(\theta)}\rvert + C = \ln|\sec\theta| + C \]
The substitution method does not always work, even when the integral looks relatively simple. For example, \(\int \sin(x^2)\, \mathrm{d}x\) cannot be evaluated explicitly by substitution, or any other method. With experience, you will learn to recognize when substitution is likely to be successful.
EXAMPLE 7 Additional Step Necessary
Evaluate \(\displaystyle \int x\sqrt{5x+1}\, \mathrm{d}x\).
Solution Since \(\sqrt{5x+1}\) appears, we are tempted to set \(u = 5x + 1\). Then \[ \mathrm{d}u = 5\, \mathrm{d}x \implies \sqrt{5x+1}\, \mathrm{d}x = \dfrac15 u^{1/2}\, \mathrm{d}u \] Unfortunately, the integrand is not \(\sqrt{5x+1}\) but \(x\sqrt{5x+1}\). To take care of the extra factor of \(x\), we solve \(u = 5x + 1\) for \(x\) to obtain \(x = \tfrac15 (u-1)\). Then \[ \begin{aligned} x \sqrt{5x+1} \, \mathrm{d}x & = \left(\dfrac15(u-1)\right)\dfrac15 u^{1/2}\, \mathrm{d}u = \dfrac1{25} (u-1)u^{1/2}\, \mathrm{d}u\\ \int x \sqrt{5x+1}\, \mathrm{d}x & =\dfrac1{25} \int (u-1)u^{1/2}\, \mathrm{d}u = \dfrac1{25} \int (u^{3/2} -u^{1/2})\, \mathrm{d}u\\ & = \dfrac1{25}\left(\dfrac25u^{5/2} - \dfrac23u^{3/2}\right) + C\\ & = \dfrac2{125} (5x+1)^{5/2} - \dfrac2{75}(5x+1)^{3/2}+C \end{aligned} \]
Change of Variables Formula for Definite Integrals
The Change of Variables Formula can be applied to definite integrals provided that the limits of integration are changed, as indicated in the next theorem.
Change of Variables Formula for Definite Integrals
\[ \boxed{\bbox[#FAF8ED,5pt]{ \displaystyle \int\limits_a^b f(u(x)) u'(x) \, \mathrm{d}x = \int\limits_{u(a)}^{u(b)} f(u)\, \, \mathrm{d}u}} \tag{2} \]
The new limits of integration with respect to the \(u\)-variable are \(u(a)\) and \(u(b)\). Think of it this way: As \(x\) varies from \(a\) to \(b\), the variable \(u = u(x)\) varies from \(u(a)\) to \(u(b)\).
332
Proof
If \(F(x)\) is an antiderivative of \(f(x)\), then \(F(u(x))\) is an antiderivative of \(f(u(x))u'(x)\). FTC I shows that the two integrals are equal: \[ \begin{aligned} \int\limits_a^b f(u(x))u'(x) \, \mathrm{d}x & = F(u(b)) - F(u(a))\\ \int\limits_{u(a)}^{u(b)} f(u) \, \mathrm{d}u & = F(u(b)) - F(u(a)) \end{aligned} \]
Change of Variables for definite integrals: \[ \int\limits_a^b f(u(x)) u'(x) \, \mathrm{d}x = \int\limits_{u(a)}^{u(b)} f(u) \, \mathrm{d}u \]
EXAMPLE 8
Evaluate \(\displaystyle \int\limits_0^2 x^2\sqrt{x^3 + 1}\, \mathrm{d}x\).
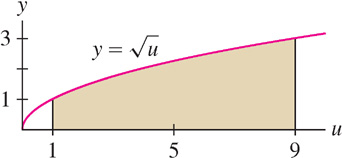
Solution Use the substitution \(u = x^{3} + 1\), \(\mathrm{d}u = 3x^{2} \, \mathrm{d}x\): \[ x^2\sqrt{x^3 + 1}\, \mathrm{d}x = \dfrac13\sqrt{u} \, \mathrm{d}u \] By Eq. (2), the new limits of integration \[ u(0) = 0^3 + 1 =1 \quad\text{and}\quad u(2) =2^3 +1 = 9 \] Thus, \[ \int\limits_0^2 x^2\sqrt{x^3 + 1}\, \mathrm{d}x = \dfrac13 \int\limits_1^9 \sqrt{u}\, \mathrm{d}u =\dfrac29u^{3/2}\bigg|_1^9 = \dfrac{52}9 \] This substitution shows that the area in Figure 5.45 is equal to one-third of the area in Figure 5.46 (but note that the figures are drawn to different scales).

Question 5.23 Substitution Progress Check Question 4
Evaluate \(\displaystyle \int\limits_0^\sqrt{3} 6x \sqrt{1+x^2} \ dx\)
In the previous example, we can avoid changing the limits of integration by evaluating the integral in terms of \(x\). \[ \int x^2\sqrt{x^3 + 1}\, \mathrm{d}x = \dfrac13 \int \sqrt{u}\, \mathrm{d}u = \dfrac29 u^{3/2} = \dfrac29 (x^3 + 1)^{3/2} \] This leads to the same result: \(\displaystyle \int x^2\sqrt{x^3 + 1}\, \mathrm{d}x = \dfrac29 (x^3 + 1)^{3/2}\bigg|_0^2 = \dfrac{52}9\).
EXAMPLE 9
Evaluate \(\displaystyle \int\limits_0^{\pi/4}\tan^3\theta\sec^2\theta\, \mathrm{d}\theta\).
Solution The substitution \(u = \tan \theta \) makes sense because \(\mathrm{d}u = \sec^{2} \theta \, \mathrm{d}\theta\) and therefore, \(u^{3} \, \mathrm{d}u = \tan^{3} \theta \sec^{2} \theta \, \mathrm{d}\theta\). The new limits of integration are \[ u(0) = \tan 0 = 0 \quad\text{and}\quad u\left(\dfrac\pi4\right)=\tan\left(\dfrac\pi4\right) = 1 \] Thus, \[ \int\limits_0^{\pi/4}\tan^3\theta\sec^2\theta\, \mathrm{d}\theta = \int\limits_0^1u^3 \, \mathrm{d}u = \dfrac{u^4}4\bigg|_0^1 = \dfrac14 \]
EXAMPLE 10
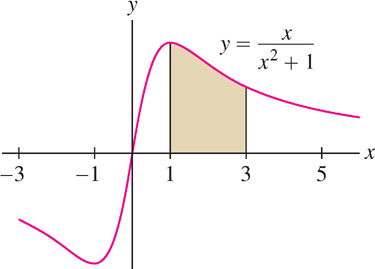
Calculate the area under the graph of \(\displaystyle y = \dfrac{x}{x^2+1}\) over \([1, 3]\).
Solution The area (Figure 5.47) is equal to \(\displaystyle \int\limits_1^3 \dfrac{x}{x^2+1}\, \mathrm{d}x\). We use the substitution
\[ u=x^2 + 1,\quad \mathrm{d}u = 2x\, \mathrm{d}x,\quad\dfrac12\dfrac{\mathrm{d}u}u = \dfrac{x\, \mathrm{d}x}{x^2 + 1} \]
333
The new limits of integration are \(u(1) = 1^{2} + 1 = 2\) and \(u(3) = 3^{2} + 1 = 10\), so \[ \int\limits_1^3 \dfrac{x}{x^2+1}\, \mathrm{d}x = \dfrac12 \int\limits_2^{10} \dfrac{\mathrm{d}u}u = \dfrac12 \ln|u|\bigg|_2^{10} = \dfrac12\ln 10 - \dfrac12\ln 2 \approx 0.805 \]
Question 5.24 Substitution Progress Check Question 5
Calculate the area under the graph of \(f(x) = \frac{1}{x \ln x}\) from \(x=e\) to \(x=e^e\).
5.6.1 Summary
- Try the Substitution Method when the integrand has the form f(u(x)) u′(x). If F is an antiderivative of f, then \[\int f(u(x))u'(x)\, dx = F(u(x)) + C\]
- The differential of u(x) is related to dx by du = u′(x) dx.
- The Substitution Method is expressed by the Change of Variables Formula: \[\int f(u(x))u'(x)\, dx = \int f(u)\, du\]
- Change of Variables Formula for definite integrals: \[\int_a^b f(u(x))u'(x)\, dx = \int_{u(a)}^{u(b)} f(u)\, du\]