6.4 The Method of Cylindrical Shells
In the previous two sections, we computed volumes by integrating cross-sectional area. The Shell Method, based on cylindrical shells, is more convenient in some cases.
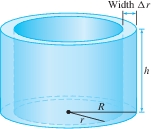
Consider a cylindrical shell (Figure 6.34) of height \(h\), with outer radius \(R\) and inner radius \(r\). Because the shell is obtained by removing a cylinder of radius \(r\) from the wider cylinder of radius \(R\), it has volume \[ \begin{equation*} \pi R^2h - \pi r^2 h = \pi h(R^2-r^2) = \pi h(R+r)(R-r) = \pi h(R+r)\Delta r \end{equation*} \] where \(\Delta r = R - r\) is the width of the shell. If the shell is very thin, then \(R\) and \(r\) are nearly equal and we may replace \((R+r)\) by \(2R\) to obtain \[ \begin{equation} \textrm{Volume of shell} \approx 2\pi Rh \Delta r = 2\pi (\textrm{radius})\times(\textrm{height of shell})\times(\textrm{thickness})\tag {1} \end{equation} \]
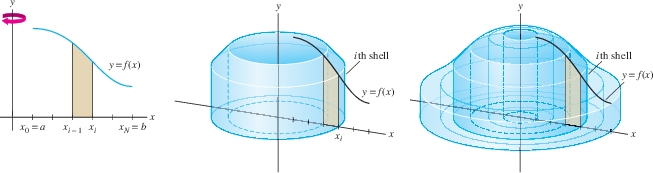
Now, let us rotate the region under \(y=f(x)\) from \(x=a\) to \(x=b\) about the \(y\)-axis as in Figure 6.35. The resulting solid can be divided into thin concentric shells. More precisely, we divide \([a,b]\) into \(N\) subintervals of length \(\Delta x= ({b-a})/{N}\) with endpoints \(x_0, x_1,\ldots ,x_N\). When we rotate the thin strip of area above \([x_{i-1},x_i]\) about the \(y\)-axis, we obtain a thin shell whose volume we denote by \(V_i\). The volume of the solid is equal to the sum \(V= \sum_{i=1}^N V_i\).
385
The top rim of the \(i\)th thin shell in Figure 6.35 is curved. However, when \(\Delta x\) is small, we can approximate this thin shell by the cylindrical shell (with flat rim) of height \(f(x_i)\). Then, using Eq. (1), we obtain \[ \begin{align} V_i &\approx 2\pi x_i f(x_i) \Delta x = 2\pi(\textrm{radius})(\textrm{height of shell})(\textrm{thickness})\notag\\ V &= \sum_{i=1}^N\,V_i \approx 2\pi\sum_{i = 1}^{N} x_i f(x_i)\Delta x\notag \end{align} \] The sum on the right is the volume of a cylindrical approximation that converges to \(V\) as \(N\to\infty\) (Figure 6.36). This sum is also a right-endpoint approximation that converges to \(2\pi\int_a^b x f(x)\, dx\). Thus we obtain Eq. (2) for the volume of the solid.
Volume of Revolution: The Shell Method
The solid obtained by rotating the region under \(y = f(x)\) over the interval \([a,b]\) about the \(y\)-axis has volume \[ \begin{equation} \boxed{\bbox[#FAF8ED,5pt]{ V = 2\pi\int_a^b\,\big(\textrm{radius}\big) \big(\textrm{height of shell}\big)\, dx = 2\pi \int_a^b xf(x)\, dx }}\tag {2} \end{equation} \]
Note: In the Shell Method, we integrate with respect to \(x\) when the region is rotated about the \(y\)-axis.
EXAMPLE 1
Find the volume \(V\) of the solid obtained by rotating the region under the graph of \(f(x) = 1 - 2x + 3x^2 - 2x^3\) over \([0,1]\) about the \(y\)-axis.
Solution The solid is shown in Figure 6.37. By Eq. (2), \[ \begin{align*} V &= 2\pi \int_0^1 x f(x)\, dx = 2\pi \int_0^1 x(1 - 2x + 3x^2 - 2x^3)\,dx\\ &= 2\pi \left(\frac12x^2 -\frac23x^3 + \frac34 x^4-\frac25x^5 \right) \bigg|_0^1 = \frac{11}{30}\pi \end{align*} \]
Question 6.9 Method of Cylindrical Shells Progress Check Question 1
suOloNLW2U3c63kqKPGIFijovokzT1Qcno0OQdvdNrv7c2NJ2rSn3h/oMN6jH9tbRSCnXFSruHd90pnK7CVxSh8YTAgRZmNO936mqmU1fUP9Xhi43abzT58M3tpiGeCXpeP5RnaU4q2HC+i5btkSDgQxHTZXzjmFPM08n87lgVNXAdZ6jjgFVIyyIjzd0Awj3GvxEtnbxfo0QROTKDSt0jl4tWiEpoI4386
CONCEPTUAL INSIGHT
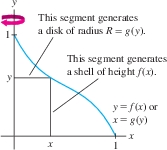
Shells versus Disks and Washers Some volumes can be computed equally well using either the Shell Method or the Disk and Washer Method, but in Example 1, the Shell Method is much easier. To use the Disk Method, we would need to know the radius of the disk generated at height \(y\) because we're rotating about the \(y\)-axis (Figure 6.38). This would require finding the inverse \(g(y) = f^{-1}(y)\). In general: Use the Shell Method if finding the shell height (which is parallel to the axis of rotation) is easier than finding the disk radius (which is perpendicular to the axis of rotation). Use the Disk Method when finding the disk radius is easier.
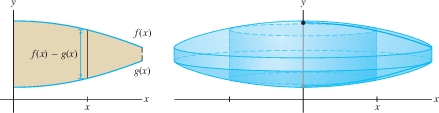
When we rotate the region between the graphs of two functions \(f(x)\) and \(g(x)\) satisfying \(f(x)\ge g(x)\), the vertical segment at location \(x\) generates a cylindrical shell of radius \(x\) and height \(f(x)-g(x)\) (Figure 6.39). Therefore, the volume is \[ \begin{align*} \boxed{\bbox[#FAF8ED,5pt]{V = 2\pi\int_a^b (\textrm{radius}) (\textrm{Height of shell})\, dx = 2\pi\int_a^b x \big(f(x) - g(x)\big) dx}} \tag {3} \end{align*} \]
EXAMPLE 2 Region Between Two Curves
Find the volume \(V\) obtained by rotating the region enclosed by the graphs of \(f(x)= x(5-x)\) and \(g(x)= 8-x(5-x)\) about the \(y\)-axis.
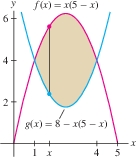
Solution First, find the points of intersection by solving \(x(5-x) = 8-x(5-x)\). We obtain \(x^2-5x+4=(x-1)(x-4)=0\), so the curves intersect at \(x=1, 4\). Sketching the graphs (Figure 6.40), we see that \(f(x)\ge g(x)\) on the interval \([1,4]\) and \[ \begin{align*} \!\textrm{Height of shell} &= f(x) - g(x) = x(5-x) - \big(8-x(5-x)\big) = 10x-2x^2-8\\ V &= 2\pi \!\int_1^4 \!(\textrm{radius})(\textrm{height of shell})\, dx\,= 2\pi\! \int_1^4 \!x (10x-2x^2-8)\, dx\\ & = 2\pi \left(\frac{10}3x^3-\frac12x^4-4x^2 \right)\bigg|_1^4= 2\pi\left(\frac{64}3 - \left(-\frac{7}6\right) \right) = 45\pi \end{align*} \]
Question 6.10 Method of Cylindrical Shells Progress Check Question 2
WJW3zmLoav2eVzN6ZgA8sZX2r9+4a6oPyFaXNYmjumq9BFqLb6aZxj8SFHoDXEY7Rbl9WEulHo5zfyIpFqIskwKgGA+pYqhV9mbDeRgUjEVmdg1ouaDf4KFhxXctx4ae0maX2tkqHtCpdR6V8+LY52TgjUFrVakihZoxHXS5j49aystMrPpns/JpT0G1MI+dDaMxw1ubSzSD0Wr45xFG7yx1lu6IL81N/MClO3Xge3fzMfGDIiTt1TsxRyr71o6OB26/2tnLyXNSz6iTv5dPvd7Lc6RQsJN8tHcxKW/4/ojrSVqSkBoMyF27o+3VEs0Gm53RN4UaLMpComildEECkJS6o3A=EXAMPLE 3 Rotating About a Vertical Axis
Use the Shell Method to calculate the volume \(V\) obtained by rotating the region under the graph of \(f(x)=x^{-1/2}\) over \([1,4]\) about the axis \(x=-3\).
Solution If we were rotating this region about the \(y\)-axis (that is, \(x=0\)), we would use Eq. (3). To rotate it around the line \(x = -3\), we must take into account that the radius of revolution is now \(3\) units longer.
The reasoning in Example 3 shows that if we rotate the region under \(y=f(x)\) over \([a,b]\) about the vertical line \(x=c\), then the volume is \begin{alignat*}{2} V&=&\;2\pi \int_a^b (x-c)f(x)\, dx\quad&\textrm{if \(c\leq a\)}\\ V&=&\;2\pi \int_a^b (c-x)f(x)\, dx\quad&\textrm{if \(c\geq b\)} \end{alignat*}
387
Figure 6.41 shows that the radius of the shell is now \(x-(-3)= x+3\). The height of the shell is still \(f(x)=x^{-1/2}\), so \[ \begin{align*} V&=2\pi\int_1^4(\textrm{radius})(\textrm{height of shell})\,dx\\ &=2\pi\int_1^4(x+3)x^{-1/2}\,dx = 2\pi\left(\frac23x^{3/2}+6x^{1/2}\right)\bigg|_1^4=\frac{64\pi}3 \end{align*} \]
The method of cylindrical shells can be applied to rotations about horizontal axes, but in this case, the graph must be described in the form \(x=g(y)\).
EXAMPLE 4 Rotating About the \(x\)-Axis
Use the Shell Method to compute the volume \(V\) obtained by rotating the region under \(y=9-x^2\) over \([0,3]\) about the \(x\)-axis.
Solution When we rotate about the \(x\)-axis, the cylindrical shells are generated by horizontal segments and the Shell Method gives us an integral with respect to \(y\). Therefore, we solve \(y=9-x^2\) for \(x\) to obtain \(x=\sqrt{9-y}\).
Segment \(\overline{AB}\) in Figure 6.42 generates a cylindrical shell of radius \(y\) and height \(\sqrt{9- y}\) (we use the term “height” even though the shell is horizontal). Using the substitution \(u=9-y\), \(du = -dy\) in the resulting integral, we obtain \[ \begin{align*} V&= 2\pi\int_0^9 (\textrm{radius})(\textrm{height of shell})\, dy = 2\pi \int_0^9 y\,\sqrt{9- y}\, dy= - 2\pi \int_9^0 (9-u)\,\sqrt u \, du \\ & = 2\pi \int_0^9 (9u^{1/2}-u^{3/2})\, du = 2\pi \left(6u^{3/2} - \frac25\,u^{5/2} \right)\bigg|_0^9 = \frac{648}5\,\pi \end{align*} \]
Reminder
After making the substitution \(u = 9 - y\), the limits of integration must be changed. Since \(u(0) = 9\) and \(u(9) = 0\), we change \(\int_0^9\) to \(\int_9^0\).
Question 6.11 Method of Cylindricl Shells Progress Check Question 3
y5ICxr97Cso1Yz9UEPBOuvaMgpZifvgUnxymowK/2xrSNuaxCH2UGC0X4fXmpAbFae+lTk/0OYEYlR6d6cC3VYxmaxswGSC8T9coYKTqe7HbqIPMmA0WdxmHJgNgUf7o8LYh4QIftnJeHOrZ3T8Sl5j3tDQ2RzUhBGYmW2cTEd+9IddVlkeQleXM2bAlZfrhk0WufZU+s7I1YgYIoTlFYva0dE4dyvQ5Im+W9oO/lDYI4QTJ25CFw30Z9C7LmPRw4AKofbmeIDixo5M6tFBIzI1vMV6xAs7ddssz8joLJa+bjEffqj+uP49sGn0f17frIKRy1Xa4QuyFuWUPlNkDXeEqlHL8TQIT+GgDZfKEOS9/iTtEy88E5J64A2sn59Vrihgy01VuPhPiQh5PIaHtZnFGjDrsm8VX0tTXmwNbivrOIWPqyKK2MBQ3Pb4RymWGq10oK6fi0+kV1+d9WOmR38Guz+nHuqXC+JUTbfmf0lqrjcmeK7R8cPGLrayEMVtoZiO6pckakXPoQ8GKE6YrKhegFkgZ7WC3LhEJwQ==388
6.4.1 Summary
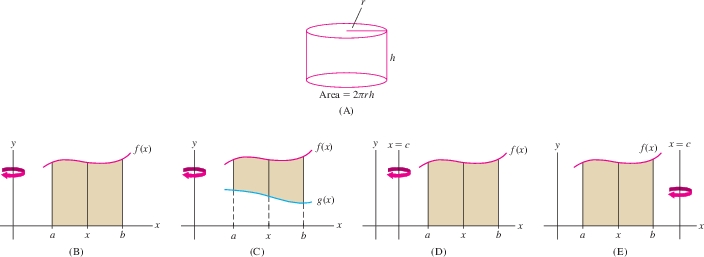
- Shell Method When you rotate the region between two graphs about an axis, the segments parallel to the axis generate cylindrical shells [Figure 6.43(A)]. The volume \(V\) of the solid of revolution is the integral of the areas of these shells: \[ \textrm{area of shell} = 2\pi (\textrm{radius})(\textrm{height of shell}) \]
- Sketch the graphs to visualize the shells.
- Figure 6.43(B): Region between \(y=f(x)\) (with \(f(x)\ge 0\)) and the \(y\)-axis, rotated about the \(y\)-axis. \[ V = 2\pi \int_a^b (\textrm{radius})(\textrm{height of shell})\, dx= 2\pi \int_a^b xf(x)\,dx \]
- Figure 6.43(C): Region between \(y=f(x)\) and \(y=g(x)\) (with \(f(x)\ge g(x)\ge 0\)), rotated about the \(y\)-axis. \[ V = 2\pi \int_a^b (\textrm{radius})(\textrm{height of shell})\, dx= 2\pi \int_a^b x(f(x) - g(x))\,dx \]
- Rotation about a vertical axis \(x=c\).
- Figure 6.43(D): \(c\le a\), radius of shell is \((x-c)\): \[ V = 2\pi \int_a^b (x-c)f(x)\, dx \]
- Figure 6.43(E): \(c\ge a\), radius of shell is \((c-x)\): \[ V = 2\pi \int_a^b (c-x)f(x)\, dx \]
- Rotation about the \(x\)-axis using the Shell Method: Write the graph as \(x=g(y)\): \[ V = 2\pi\int_c^d(\textrm{radius})(\textrm{height of shell})\,dy = 2\pi\int_c^d yg(y)\,dy \]
389