7.6 Improper Integrals
The integrals we have studied so far represent signed areas of bounded regions. However, areas of unbounded regions (Figure 7.8) also arise in applications and are represented by improper integrals.
There are two ways an integral can be improper: (1) The interval of integration may be infinite, or (2) the integrand may tend to infinity. We deal first with improper integrals over infinite intervals. One or both endpoints may be infinite: \[ \int_{-\infty}^a f(x)\, dx,\qquad \int_a^{\infty} f(x)\, dx, \qquad \int_{-\infty}^{\infty} f(x)\,dx \]
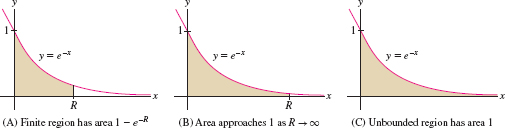
How can an unbounded region have finite area? To answer this question, we must specify what we mean by the area of an unbounded region. Consider the area [Figure 7.9] under the graph of \(f(x)=e^{-x}\) over the finite interval \([0,R]\): \[ \int_0^R e^{-x}\,dx = -e^{-x}\bigg|_0^R = -e^{-R} + e^{0} = 1 - e^{-R} \]
As \(R\to\infty\), this area approaches a finite value [Figure 7.9]: \[ \int_0^{\infty} e^{-x}\,dx = \lim_{R\to\infty} \int_0^R e^{-x}\,dx = \lim_{R\to\infty} \big(1 - e^{-R}\big) = 1\tag{1} \]
The great British mathematician G. H. Hardy (1877–1947) observed that in calculus, we learn to ask, not “ What is it?” but rather “How shall we define it?” We saw that tangent lines and areas under curves have no clear meaning until we define them precisely using limits. Here again, the key question is “How shall we define the area of an unbounded region?”
It seems reasonable to take this limit as the definition of the area under the graph over the infinite interval \([0,\infty)\). Thus, the unbounded region in Figure 7.9 has area 1.
437
DEFINITION Improper Integral
Fix a number \(a\) and assume that \(f(x)\) is integrable over \([a,b]\) for all \(b> a\). The improper integral of \(f(x)\) over \([a,\infty)\) is defined as the following limit (if it exists): \[ \int_a^\infty f(x)\,dx = \lim_{R\to\infty} \int_a^R f(x)\,dx \]
We say that the improper integral converges if the limit exists (and is finite) and that it diverges if the limit does not exist.
Similarly, we define \[ \int_{-\infty}^a f(x)\,dx= \lim_{R\to-\infty} \int_R^a f(x)\,dx \]
A doubly infinite improper integral is defined as a sum (provided that both integrals on the right converge): \[ \int_{-\infty}^\infty f(x)\, dx = \int_{-\infty}^0 f(x)\, dx + \int_0^{\infty} f(x)\, dx\tag{2} \]
EXAMPLE 1
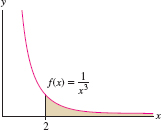
Show that \(\int_2^{\infty} \dfrac{dx}{x^3}\) converges and compute its value.
Solution
Step 1. Integrate over a finite interval \([2,R]\). \[ \int_2^R \frac{dx}{x^3} = -\frac12x^{-2}\bigg|_2^R= -\frac12\big(R^{-2}\big) + \frac12\big(2^{-2}\big) = \frac18-\frac1{2R^2} \]
Step 2. Compute the limit as \(R\to\infty\). \[ \int_2^{\infty} \frac{dx}{x^3} = \lim_{R\to\infty} \int_2^R \frac{dx}{x^3} = \lim_{R\to\infty}\left( \frac18-\frac1{2R^2}\right) = \frac18 \]
We conclude that the infinite shaded region in Figure 7.10 has area \(\frac18\).
Question 7.13 Improper Integrals Progress Check Question 1
Evaluate \( \int \limits_1^\infty \dfrac{1}{x^2} \ dx\)
EXAMPLE 2
Determine whether \(\displaystyle \int_{-\infty}^{-1} \dfrac{dx}x\) converges.
Solution First, we evaluate the definite integral over a finite interval \([R,-1]\) Since the lower limit of the integral is \(-\infty\), we take \(R<-1\): \[ \int_{R}^{-1} \frac{dx}x = \ln |x|\bigg|_{R}^{-1} = \ln \left|-1\right| - \ln |R| = -\ln |R| \]
Then we compute the limit as \(R\to -\infty\): \[ \lim_{R\to-\infty} \int_{R}^{-1} \frac{dx}x = \lim_{R\to-\infty} \left( -\ln |R| \right) = - \lim_{R\to-\infty} \ln |R| = -\infty \]
The limit is infinite, so the improper integral diverges. We conclude that the area of the unbounded region in Figure 7.11 is infinite.

438
CONCEPTUAL INSIGHT
If you compare the unbounded shaded regions in Figures Figure 7.10 and Figure 7.11, you may wonder why one has finite area and the other has infinite area. Convergence of an improper integral depends on how rapidly the function \(f(x)\) tends to zero as \(x\to\infty\) (or \(x\to -\infty\)). Our calculations show that \(x^{-2}\) decreases rapidly enough for convergence, whereas \(x^{-1}\) does not.
An improper integral of a power function \(f(x) = x^{-p}\) is called a p-integral. Note that \(f(x)=x^{-p}\) decreases more rapidly as \(p\) gets larger. Interestingly, our next theorem shows that the value \(p=1\) is the dividing line between convergence and divergence.
THEOREM 1
The \(p\)-Integral over \([a,\infty)\)] For \(a>0\), \[ \begin{align*} \int_a^{\infty} \frac{dx}{x^p} = \begin{cases} \dfrac{a^{1-p}}{p-1}& \text{if \(p > 1\)} \\ \textrm{diverges}& \text{if \(p \le 1\)} \end{cases} \end{align*} \]
\(p\)-integrals are particularly important because they are often used to determine the convergence or divergence of more complicated improper integrals by means of the Comparison Test (see Example 8).
Proof
Denote the \(p\)-integral by \(J\). Then \[ J= \lim_{R\to\infty}\int_a^Rx^{-p}\,dx =\lim_{R\to\infty}\frac{x^{1-p}}{1-p}\bigg|_a^R =\lim_{R\to\infty}\left(\frac{R^{1-p}}{1-p} -\frac{a^{1-p}}{1-p}\right) \]
If \(p>1\), then \(1-p<0\) and \(R^{1-p}\) tends to zero as \(R\to\infty\). In this case, \(J= \frac{a^{1-p}}{p-1}\). If \(p<1\), then \(1-p>0\) and \(R^{1-p}\) tends to \(\infty\). In this case, \(J\) diverges. If \(p=1\), then \(J\) diverges because \(\lim\limits_{R\to\infty}\int_a^R x^{-1}\,dx = \lim\limits_{R\to\infty}(\ln R - \ln a) = \infty\).
Sometimes it is necessary to use L'Hôpital's Rule to determine the limits that arise in improper integrals.
EXAMPLE 3 Using L'Hôpital's Rule
Calculate \(\displaystyle\int_{0}^{\infty} xe^{-x}\, dx\).
Solution First, use Integration by Parts with \(u=x\) and \(v'=e^{-x}\): \[ \begin{eqnarray*} \int xe^{-x}\, dx &=& -xe^{-x} + \int e^{-x}\, dx = -xe^{-x}-e^{-x} = -(x+1)e^{-x} + C\\ \int_0^R xe^{-x}\, dx &=&-(x+1)e^{-x}\bigg|_0^R = -(R+1)e^{-R} + 1 = 1-\frac{R+1}{e^R} \end{eqnarray*} \]
Then compute the improper integral as a limit using L'Hôpital's Rule: \[ \int_0^{\infty} xe^{-x}\, dx = 1 - \lim_{R\to \infty} \frac{R+1}{e^R} = 1 - \underbrace{\lim_{R\to \infty} \frac{1}{e^R}}_{\textrm{L'Hôpital's Rule}} =1-0=1 \]
Question 7.14 Improper Integrals Progress Check Question 2
Determine if \(\displaystyle \int \limits_1^\infty x^{-\frac{4}{5}} \ dx\) converges or diverges. If the integral converges, find its value.
| A. |
| B. |
| C. |
| D. |
439
440
Infinite Discontinuities at the Endpoints
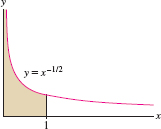
An integral over a finite interval \([a,b]\) is improper if the integrand becomes infinite at one or both of the endpoints of the interval. In this case, the region in question is unbounded in the vertical direction. For example, \(\int_0^1 \frac{dx}{\sqrt x}\) is improper because the integrand \(f(x) = x^{-1/2}\) tends to \(\infty\) as \(x\to 0+\) (Figure 7.12). Improper integrals of this type are defined as one-sided limits.
DEFINITION Integrands with Infinite Discontinuities
If \(f(x)\) is continuous on \([a,b)\) but discontinuous at \(x=b\), we define \[ \int_a^b f(x)\, dx = \lim_{R\to b-} \int_a^R f(x)\, dx \]
Similarly, if \(f(x)\) is continuous on \((a,b]\) but discontinuous at \(x=a\), \[ \int_a^b f(x)\, dx = \lim_{R\to a+} \int_R^b f(x)\, dx \]
In both cases, we say that the improper integral converges if the limit exists and that it diverges otherwise.
EXAMPLE 4
Calculate: (a) \(\displaystyle\int_0^9\dfrac{dx}{\sqrt x}\quad\) and\(\quad\)(b) \(\displaystyle\int_0^{1/2}\dfrac{dx}{x}\).
Solution Both integrals are improper because the integrands have infinite discontinuities at \(x=0\). The first integral converges: \[ \begin{align*} \int_0^9 \frac{dx}{\sqrt{x}} &= \lim_{R\to 0+}\int_R^9 \,x^{-1/2} dx = \lim_{R\to 0+}2x^{1/2}\bigg|_R^9\\ &= \lim_{R\to 0+}(6-2R^{1/2})=6 \end{align*} \]
The second integral diverges: \[ \begin{align*} \int_0^{1/2}\dfrac{dx}{x} &= \lim_{R\to 0+} \int_R^{1/2}\frac{dx}{x} = \lim_{R\to 0+} \left(\ln \frac12 - \ln R \right) \\ &=\ln \frac12 - \lim_{R\to 0+} \ln R = \infty \end{align*} \]
The proof of the next theorem is similar to the proof of Theorem 1 (see Exercise 52).
Theorem 2 is valid for all exponents \(p\). However, the integral is not improper if \(p<0\).
THEOREM 2 The \(p\)-Integral over \(\lbrack 0,a\rbrack\)
For \(a >0\), \[ \int_0^a \frac{dx}{x^p} = \begin{cases} \dfrac{a^{1-p}}{1-p}& \text{if \(p < 1\)} \\ \textrm{diverges} &\text{if \(p \ge 1\)} \end{cases} \]
Question 7.15 Improper Integrals Progress Check Question 4
Evaluate \( \int \limits_0^1 \dfrac{1}{\sqrt{x}} \ dx\)
441
GRAPHICAL INSIGHT
The \(p\)-integrals \(\int_a^\infty\,x^{-p}\, dx\) and \(\int_0^a\,x^{-p}\, dx\) have opposite behavior for \(p\ne 1\). The first converges only for \(p>1\), and the second converges only for \(p<1\) (both diverge for \(p=1\)). This is reflected in the graphs of \(y=x^{-p}\) and \(y = x^{-q}\), which switch places at \(x=1\) (Figure 7.13). We see that a large value of \(p\) helps \(\int_a^\infty\,x^{-p}\, dx\) to converge but causes \(\int_0^a\,x^{-p}\, dx\) to diverge.
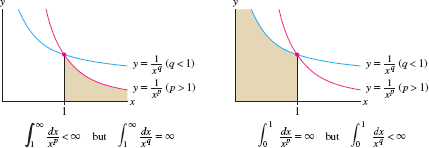
In Section 9.1, we will compute the length of a curve as an integral. It turns out that the improper integral in our next example represents the length of one-quarter of a unit circle. Thus, we can expect its value to be \(\frac14(2\pi) =\pi/2\).
EXAMPLE 5
Evaluate \(\displaystyle\int_0^1\dfrac{dx}{\sqrt{1 - x^2}}\).
Solution This integral is improper with an infinite discontinuity at \(x=1\) (Figure 7.14). Using the formula \({\int \frac{dx}{\sqrt{1-x^2}}=\sin^{-1}x + C}\), we find \[ \begin{align*} \int_0^1\frac{dx}{\sqrt{1-x^2}} &= \lim_{R\to 1-}\int_0^R\frac{dx}{\sqrt{1-x^2}}\\ &=\lim_{R\to 1-}(\sin^{-1}R-\sin^{-1}0)\\ &= \sin^{-1}1-\sin^{-1}0 =\frac{\pi}2-0=\frac{\pi}2 \end{align*} \]

Comparing Integrals
Sometimes we are interested in determining whether an improper integral converges, even if we cannot find its exact value. For instance, the integral \[ \int_1^{\infty} \frac{e^{-x}}{x} \, dx \]
cannot be evaluated explicitly. However, if \(x\geq 1\), then \[ 0 \leq \frac{1}{x} \leq 1\quad\Rightarrow\quad 0 \leq \frac{e^{-x}}{x} \leq e^{-x} \]
In other words, the graph of \(y = e^{-x}/x\) lies underneath the graph of \(y= e^{-x}\) for \(x\ge 1\) (Figure 7.15). Therefore \[ {0\quad\le\quad \int_1^{\infty} \frac{e^{-x}}{x}} \, dx \quad\le \underbrace{\int_1^{\infty} e^{-x} \, dx =e^{-1}}_{\textrm{Converges by direct computation}} \]
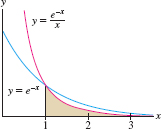
442
Since the larger integral converges, we can expect that the smaller integral also converges (and that its value is some positive number less than \(e^{-1}\)). This type of conclusion is stated in the next theorem. A proof is provided in a supplement on the text's Companion Web Site.
THEOREM 3 Comparison Test for Improper Integrals
Assume that \(f(x) \ge g(x) \geq 0\) for \(x \ge a\).
- If \(\displaystyle\int_a^{\infty} f(x)\, dx\) converges, then \(\displaystyle\int_a^{\infty} g(x)\, dx\) also converges.
- If \(\displaystyle\int_a^{\infty} g(x)\, dx\) diverges, then \(\displaystyle\int_a^{\infty} f(x)\, dx\) also diverges.
The Comparison Test is also valid for improper integrals with infinite discontinuities at the endpoints.
What the Comparison Test says (for nonnegative functions):
- If the integral of the bigger function converges, then the integral of the smaller function also converges.
- If the integral of the smaller function diverges, then the integral of the larger function also diverges.
EXAMPLE 6
Show that \(\int_1^{\infty} \dfrac{dx}{\sqrt{x^3 + 1}}\) converges.
Solution We cannot evaluate this integral, but we can use the Comparison Test. To show convergence, we must compare the integrand \((x^3+1)^{-1/2}\) with a larger. function whose integral we can compute.
It makes sense to compare with \(x^{-3/2}\) because \(\sqrt{x^3} \le \sqrt{x^3 + 1}\), and therefore \[ \frac{1}{\sqrt{x^3 + 1}}\le \frac{1}{\sqrt{x^3}}={x^{-3/2}} \]
The integral of the larger function converges, so the integral of the smaller function also converges: \[ \underbrace{\int_1^{\infty} \dfrac{dx}{x^{3/2}}}_{\textrm{\(p\)-integral with \(p>1\)}}~ \textrm{converges}\quad \Rightarrow\quad \underbrace{\int_1^{\infty} \dfrac{dx}{\sqrt{x^3 + 1}}}_{\textrm{Integral of smaller function }}~\textrm{converges} \]
EXAMPLE 7 Choosing the Right Comparison
Does \(\displaystyle\int_1^{\infty} \dfrac{dx}{\sqrt x + e^{3x}}\) converge?
Solution Since \(\sqrt{x} \geq 0\), we have \(\sqrt{x} + e^{3x} \geq e^{3x}\) and therefore \[\frac{1}{\sqrt{x} + e^{3x}} \leq \frac{1}{e^{3x}} \]
Furthermore, \[ \int^\infty_1 \dfrac{dx}{e^{3x}} = \left.\lim_{R\to\infty} -\frac13 e^{-3x}\right|^{R}_1 = \lim_{R\to\infty} \frac13 \big(e^{-3} -e^{-3R}\big) = \frac{1}{3} e^{-3}\quad\textrm{(converges)}\]
Our integral converges by the Comparison Test: \[ \underbrace{\int_1^{\infty} \dfrac{dx}{e^{3x}}}_{\textrm{Integral of larger function}}\quad \textrm{converges}\quad \Rightarrow\quad \underbrace{\int_1^{\infty}\dfrac{dx}{\sqrt x + e^{3x}}}_{\textrm{Integral of smaller function}} \quad\textrm{also converges} \]
Had we not been thinking, we might have tried to use the inequality \[ \frac{1}{\sqrt x + e^{3x}} \le \frac{1}{\sqrt x} \]
443
However,\(\int_1^{\infty} \frac{dx}{\sqrt x}\) diverges (\(p\)-integral with \(p<1\)), and this says nothing about our smaller integral (Figure 7.16).

EXAMPLE 8 Endpoint Discontinuity
Does \(J = \displaystyle\int_0^{0.5} \dfrac{dx}{x^{8} + x^{2}}\) converge?
Solution This integral has a discontinuity at \(x=0\). We might try the comparison \[ x^{8} + x^{2} > x^{2} \quad \Rightarrow \quad \frac1{x^{8} + x^{2}} < \frac1{x^{2}} \]
However, the \(p\)-integral \(\int_0^{0.5} \frac{dx}{x^{2}}\) diverges, so this says nothing about our integral \(J\), which is smaller. But notice that if \(0 < x <0.5\), then \(x^8<x^2\), and therefore \[ x^{8} + x^{2} <2 x^{2} \quad \Rightarrow \quad \frac1{x^{8} + x^{2}} > \frac{1}{2x^{2}} \]
Since \(\int_0^{0.5} \frac{dx}{2x^{2}}\) diverges, the larger integral \(J\) also diverges.
7.6.1 Summary
- An improper integral is defined as the limit of ordinary
integrals:
\[
\int_a^{\infty} f(x)\,dx = \lim_{R\to\infty} \int_a^R f(x)\,dx
\]
The improper integral converges if this limit exists, and it diverges otherwise.
- If \(f(x)\) is continuous on \([a,b)\) but discontinuous at \(x=b\), then \[ \int_a^b f(x)\,dx = \lim_{R\to b-} \int_a^R f(x)\,dx \]
- An improper integral of \(x^{-p}\) is called a \(p\)-integral. For \(a>0\), \[ \boxed{\bbox[#FAF8ED,5pt]{ \begin{align*} p>1: & \displaystyle\int_a^\infty\frac{dx}{x^p}\quad \text{converges}&\text{and}&\quad \displaystyle\int_0^a\frac{dx}{x^p}\quad \text{diverges}\\ p<1: & \displaystyle\int_a^\infty\frac{dx}{x^p}\quad \text{diverges}&\text{and}&\quad \displaystyle\int_0^a\frac{dx}{x^p}\quad \text{converges}\\ p = 1: & \displaystyle\int_a^\infty \frac{dx}{x}\quad \text{and}\quad \displaystyle\int_0^a \frac{dx}{x}\quad \text{both diverge} \end{align*}}} \]
- The Comparison Test: Assume that \(f(x)\ge g(x)\ge 0\) for \(x \geq a\).
Then:
\[
\begin{align*}
\text{If}\quad \displaystyle\int_a^\infty f(x)\,dx~\text{converges}, \quad & \text{then} & \displaystyle\int_a^\infty g(x)\,dx~\text{converges}.\\
\\
\text{If}\quad \displaystyle\int_a^\infty g(x)\,dx~\text{diverges}, \quad & \text{then} & \displaystyle\int_a^\infty f(x)\,dx~\text{diverges}.
\end{align*}
\]
444
- Remember that the Comparison Test provides no information if the larger integral \(\int_a^\infty f(x)\,dx\) diverges or the smaller integral \(\int_a^\infty g(x)\,dx\) converges.
- The Comparison Test is also valid for improper integrals with infinite discontinuities at endpoints.