Question 2.199

Describe the graphs of:

• (a) \(f (x,y) = 3x^2 + y^2\)
• (b) \(f (x,y) = xy + 3x\)

Question 2.200

Describe some appropriate level surfaces and sections of the graphs of:

• (a) \(f (x,y,z) = 2x^2 + y^2 + z^2\)
• (b) \(f (x,y,z) = x^2\)
• (c) \(f (x,y,z) = xyz\)

Question 2.201

Compute the derivative \({\bf D}\! f ({\bf x})\) of each of the following functions:

• (a) \(f (x,y) = (x^2 y, e^{-xy})\)
• (b) \(f (x) = (x,x)\)
• (c) \(f (x,y,z) = e^x + e^y + e^z\)
• (d) \(f (x,y,z) = (x,y,z)\)

Question 2.202

Suppose \(f (x,y) = f(y,x)\) for all \((x,y)\). Prove that \[ ( \partial f / \partial x) (a,b)= ( \partial f / \partial y) (b,a). \]

Question 2.203

Let \(f(u, v)=(\cos u, v+\sin u)\) and \(g(x, y, z)=(x^2+\pi y^2, xz)\). Compute \(D(f \circ g)\) at (0, 1, 1) using the chain rule.

Question 2.204

Use the chain rule to find \(D(f \circ g)(-2, 1)\) for \(f(u, v, w)=(v^2+uw, u^2+w^2, u^2v-w^3)\) and \(g(x, y)=(xy^3, x^2-y^2, 3x+5y)\).

Question 2.205

Use the chain rule to find \(D(f \circ g)(-1, 2)\) for \(f(u, v, w)=(v^2+w^2, u^3-vw, u^2v+w)\) and \(g(x, y)=(3x+2y, x^3y, y^2-x^2)\).

Question 2.206

Let \(f(x, y)=(xy, \frac{x}{y}, x+y)\) and \(g(w, s, t)=(we^s, se^{wt})\). Find \(D(f \circ g)(3, 1, 0)\).

Question 2.207

Let \(\textbf{r}(t)=(t\cos(\pi t), t\sin(\pi t), t)\) be a path. Where will the tangent line to \(\textbf{r}\) at \(t=5\) intersect the \(xy\) plane?

Question 2.208

Let \(f(x, y)=x^2e^{-xy}\).

• (a) Find a vector normal to the graph of \(f\) at (1, 2).
• (b) Find the equation of the tangent plane to the graph of \(f\) at (1, 2).
• (c) What point on the surface given by \(z=x^2-y^2\) has a tangent plane parallel to the plane found in (b)?

Question 2.209

Let \(f(x,y) = (1- x^2 - y^2)^{1/2}\). Show that the plane tangent to the graph of \(f\) at \((x_0, y_0, f (x_0, y_0))\) is orthogonal to the vector \((x_0, y_0 ,f (x_0, y_0))\). Interpret geometrically.

Question 2.210

Let \(F(u,v)\) and \(u=h(x,y,z)\), \(v=k(x,y,z)\) be given (differentiable) real-valued functions and let \(f(x,y,z)\) be defined by \(f(x,y,z)=F(h(x,y,z)\), \(k(x,y,z))\). Write a formula for the gradient of \(f\) in terms of the partial derivatives of \(F, h\), and \(k\).

Question 2.211

Find an equation for the tangent plane of the graph of \(f\) at the point \((x_0, y_0, f (x_0, y_0))\) for:

• (a) \(f\colon\, {\mathbb R}^2 \to {\mathbb R}, (x,y) \mapsto x - y +2, (x_0, y_0) = (1,1)\)
• (b) \(f\colon\, {\mathbb R}^2 \to {\mathbb R}, (x,y) \mapsto x^2 + 4 y^2, (x_0, y_0) = (2,-1)\)
• (c) \(f\colon\, {\mathbb R}^2 \to {\mathbb R}, (x,y) \mapsto xy, (x_0, y_0) = (-1,-1)\)
• (d) \(f (x,y) =\, \log\, (x+y)+ x \cos y + \arctan (x+y), (x_0, y_0) = (1,0)\)
• (e) \(f (x,y) = \sqrt{x^2 + y^2},\qquad (x_0, y_0) = (1,1)\)
• (f) \(f (x,y) = xy,\qquad (x_0, y_0) = (2,1)\)

Question 2.212

Compute an equation for the tangent planes of the following surfaces at the indicated points.

• (a) \(x^2 + y^2 + z^2 =3, \qquad\quad (1,1,1)\)
• (b) \(x^3 - 2 y^3 + z^3 =0, \qquad (1,1,1)\)
• (c) \((\cos x) ( \cos y) e^z =0, (\pi /2, 1,0)\)
• (d) \(e^{xyz} =1, (1,1,0)\)

Question 2.213

Draw some level curves for the following functions:

• (a) \(f(x,y) = 1 /xy\)
• (b) \(f(x,y) = x^2 - xy - y^2\)

Question 2.214

Consider a temperature function \(T (x,y)= x \sin y\). Plot a few level curves. Compute \(\nabla T\) and explain its meaning.

Question 2.215

Find the following limits if they exist:

• (a) \({\rm limit}_{(x,y) \to (0,0)} \frac{\cos xy-1}{x}\)
• (b) \({\rm limit}_{(x,y)\to (0,0)}\sqrt{|(x+y) / (x-y)|}, x \ne y\)

Question 2.216

Compute the first partial derivatives and gradients of the following functions:

• (a) \(f(x,y,z) = xe^z + y \cos x\)
• (b) \(f (x,y,z) = (x+ y + z)^{10}\)
• (c) \(f (x,y,z) = (x^2 + y) /z\)

Question 2.217

Compute \(\displaystyle\frac{\partial}{\partial x}[x\exp\,(1+x^2+y^2)]\)

145

Question 2.218

Let \(f \colon \mathbb{R}^2 \to \mathbb{R}^4\) and \(g \colon \mathbb{R}^2 \to \mathbb{R}^2\) be given by \(f(x, z)=(x^2-y^2, 0, \sin(xy), 1)\) and \(g(x, y)=(ye^{x^2}, xe^{y^2})\). Compute \(D(f \circ g)(1, 2)\).

Question 2.219

Let \(f(x, y)=(x^2+y^2)e^{-(x^2+y^2+10)}\). Find the rate of change of \(f\) at (2, 1) in the direction pointing toward the origin.

Question 2.220

Let \(y (x)\) be a differentiable function defined implicitly by \(F (x,y(x)) =0\). From Exercise 19(a), Section 2.6, we know that \[ \frac{dy}{dx} = - \frac{ \partial F / \partial x}{ \partial F/ \partial y}. \]

Consider the surface \(z = F (x,y)\), and suppose \(F\) is increasing as a function of \(x\) and as a function of \(y\); that is, \(\partial F/ \partial x > 0\) and \(\partial F / \partial y > 0\). By considering the graph and the plane \(z=0\), show that for \(z\) fixed at \(z=0\), \(y\) should decrease as \(x\) increases and \(x\) should decrease as \(y\) increases. Does this agree with the minus sign in the formula for \(dy/dx\)?

Question 2.221

• Consider the graph of a function \(f (x,y)\) [Figure 2.56]. Let \((x_0, y_0)\) lie on a level curve \(C\), so \(\nabla \! f (x_0, y_0)\) is perpendicular to this curve. Show that the tangent plane of the graph is the plane that (i) contains the line perpendicular to \(\nabla \! f (x_0, y_0)\) and lying in the horizontal plane \(z = f (x_0, y_0)\), and (ii) has slope \( \| \nabla \! f (x_0, y_0) \|\) relative to the \(xy\) plane.

  

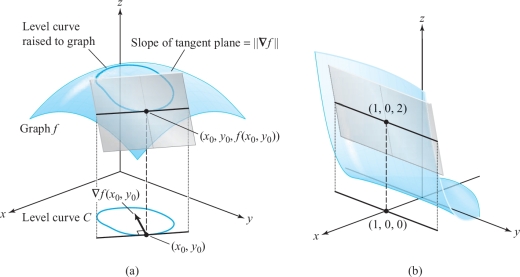  Figure 2.56: (a) The relationship between the gradient of a function and the tangent plane to the graph [Exercise 23(a)]. For a specific instance of the tangent plane in (b) see Exercise 23(b).

  (By the slope of a plane \(P\) relative to the \(xy\) plane we mean the tangent of the angle \(\theta, 0 \le \theta \le \pi\), between the upward-pointing normal \({\bf p}\) to \(P\) and the unit vector \({\bf k}\).)

• Use this method to show that the tangent plane of the graph of \(f (x,y) = (x + \cos y) x^2\) at \((1, 0, 2)\) is as sketched in Figure 2.56.

Question 2.222

Find the plane tangent to the surface \(z = x^2 + y^2\) at the point \((1, -2,5)\). Explain the geometric significance, for this surface, of the gradient of \(f (x,y) = x^2 + y^2\) (see Exercise 23).

Question 2.223

In which direction is the directional derivative of \(f (x,y) = (x^2 - y^2) / (x^2 + y^2)\) at (1, 1) equal to zero?

Question 2.224

Find the directional derivative of the given function at the given point and in the direction of the given vector.

• (a) \(f(x,y,z) = e^x \cos (yz),\qquad p_0 = (0,0,0), {\bf v}= (2,1,-2)\)
• (b) \(f(x,y,z) = xy + yz + zx,\qquad p_0 = (1,1,2), {\bf v} = (10, -1, 2)\)

Question 2.225

Find the tangent plane and normal to the hyperboloid \(x^2 + y^2 - z^2 = 18\) at \((3,5,-4)\).

Question 2.226

Let \((x (t), y(t))\) be a path in the plane, \(0 \le t \le 1\), and let \(f(x,y)\) be a \(C^1\) function of two variables. Assume that \((dx/dt)f_x+(dy/dt)f_y \le 0\). Show that \(f (x (1), y (1)) \le f (x (0), y(0))\).

146

Question 2.227

A bug finds itself in a toxic environment. The toxicity level is given by \(T (x,y) = 2x^2 - 4y^2\). The bug is at \((-1,2)\). In what direction should it move to lower the toxicity the fastest?

Question 2.228

Find the direction in which the function \(w = x^2 + xy\) increases most rapidly at the point \((-1,1)\). What is the magnitude of \(\nabla w\) at this point? Interpret this magnitude geometrically.

Question 2.229

Let \(f\) be defined on an open set \(S\) in \({\mathbb R}^n\). We say that \(f\) is homogeneous of degree \(p\) over \(S\) if \(f ( \lambda {\bf x})= \lambda^p f({\bf x})\) for every real \(\lambda\) and for every \({\bf x}\) in \(S\) for which \(\lambda {\bf x} \in S\).

• (a) If such a function is differentiable at \({\bf x}\), show that \({\bf x}\,{ \cdot}\, \nabla \! f ({\bf x})= pf ( {\bf x})\). This is known as Euler’s theorem for homogeneous functions. [HINT: For fixed x, define \(g ( \lambda)= f ( \lambda {\bf x})\) and compute \(g'(1)\).]
• (b) Find \(p\) and check Euler’s theorem for the function \(f (x,y,z) = x- 2y - \sqrt{xz},\) on the region where \(xz > 0\).

Question 2.230

If \(z= [ f(x-y) ]/y\) (where \(f\) is differentiable and \(y\neq 0\)), show that the identity \(z + y( \partial z / \partial x) + y ( \partial z / \partial y) =0\) holds.

Question 2.231

Given \(z= f((x +y)/ (x-y))\) for \(f\) a \(C^1\) function, show that \[ x \frac{\partial z}{\partial x} + y \frac{\partial z}{ \partial y} =0. \]

Question 2.232

Let \(f\) have partial derivatives \(\partial f ( {\bf x}) / \partial x_i\), where \(i=1,2, \ldots , n\), at each point \({\bf x}\) of an open set \(U\) in \({\mathbb R}^n\). If \(f\) has a local maximum or a local minimum at the point \({\bf x}_0\) in \(U\), show that \(\partial f ({\bf x}_0) / \partial x_i =0\) for each \(i\).

Question 2.233

Consider the functions defined in \({\mathbb R}^2\) by the following formulas:

• (i) \(f(x,y) = xy / (x^2 + y^2) \quad \hbox{if} \quad (x,y) \ne (0,0), f (0,0) =0\)
• (ii) \(f(x,y) = x^2y^2 / (x^2 + y^4) \quad \hbox{if} \quad (x,y) \ne (0,0), f (0,0) =0\)

• (a) In each case, show that the partial derivatives \(\partial f (x,y)/ \partial x\) and \(\partial f (x,y)/ \partial y\) exist for every \((x,y)\) in \({\mathbb R}^2\), and evaluate these derivatives explicitly in terms of \(x\) and \(y\).
• (b) Explain why the functions described in (i) and (ii) are or are not differentiable at (0, 0).

Question 2.234

Compute the gradient vector \(\nabla \! f(x,y)\) at all points \((x,y)\) in \({\mathbb R}^2\) for each of the following functions:

• (a) \(f(x,y) = x^2 y^2 \log\, ( x^2 + y^2 ) \quad \hbox{if} (x,y) \ne (0,0), f (0,0) =0\)
• (b) \(f(x,y) = x y \sin\, [1 / (x^2 + y^2 )] \quad \hbox{if} (x,y) \ne (0,0), \qquad f (0,0) =0\)

Question 2.235

Find the directional derivatives of the following functions at the point \((1, 1)\) in the direction \(({\bf i} + {\bf j})/ \sqrt{2}\):

• (a) \(f(x,y) = x \tan^{-1}\, (x/y)\)
• (b) \(f(x,y) = \cos\, (\sqrt{x^2 + y^2})\)
• (c) \(f(x,y) = \exp\, (-x^2 - y^2)\)

Question 2.236

• (a) Let \({\bf u} = {\bf i} - 2 {\bf j} +2 {\bf k}\) and \({\bf v} = 2 {\bf i} + {\bf j} - 3 {\bf k}\). Find: \(\| {\bf u} \| , {\bf u}\,{ \cdot}\,{\bf v},{\bf u} \times {\bf v}\), and a vector in the same direction as \({\bf u}\), but of unit length.
• (b) Find the rate of change of \(e^{xy} \sin (xyz)\) in the direction \({\bf u}\) at \((0, 1, 1)\).

Question 2.237

Let \(h (x,y) = 2 e^{-x^2} + e^{-3y^2}\) denote the height on a mountain at position \((x,y)\). In what direction from \((1, 0)\) should one begin walking in order to climb the fastest?

Question 2.238

Compute an equation for the plane tangent to the graph of \[ f(x,y) = \frac{e^x}{x^2 + y^2} \] at \(x=1, y=2\).

Question 2.239

• (a) Give a careful statement of the general form of the chain rule.
• (b) Let \(f(x,y) = x^2 + y\) and \({\bf h} (u)= ( \sin 3u, \cos 8u)\). Let \(g(u) = f({\bf h} (u))\). Compute \(dg/du\) at \(u=0\) both directly and by using the chain rule.

Question 2.240

• (a) Sketch the level curves of \(f(x,y) = - x^2 - 9 y^2\) for \(c=0, -1,-10.\)
• (b) On your sketch, draw in \(\nabla \! f\) at \((1,1)\). Discuss.

Question 2.241

At time \(t=0\), a particle is ejected from the surface \(x^2 + 2 y^2 + 3 z^2 =6\) at the point \((1, 1, 1)\) in a direction normal to the surface at a speed of 10 units per second. At what time does it cross the sphere \(x^2 + y^2 + z^2 =103\)?

Question 2.242

At what point(s) on the surface in Exercise 43 is the normal vector parallel to the line \(x=y=z\)?

Question 2.243

Compute \(\partial z / \partial x\) and \(\partial z / \partial y\) if \[ z = \frac{u^2 + v^2}{u^2 - v^2}, \qquad u = {\mathop e}^{-x-y}, \qquad v = e^{xy} \] (a) by substitution and direct calculation, and (b) by the chain rule.

147

Question 2.244

Compute the partial derivatives as in Exercise 45 if \(z= uv, u = x+y,\) and \(v=x-y\).

Question 2.245

What is wrong with the following argument? Suppose that \(w = f(x,y)\) and \(y = x^2\). By the chain rule, \[ \frac{\partial w}{\partial x} = \frac{\partial w}{\partial x} \frac{\partial x}{\partial x} + \frac{\partial w\, \partial y}{\partial y\, \partial x} = \frac{\partial w}{\partial x} + 2x \frac{\partial w}{\partial y} . \]

Hence, \(0 = 2x ( \partial w/ \partial y)\), and so \(\partial w / \partial y =0\). Choose an explicit example to really see that this is incorrect.

Question 2.246

A boat is sailing northeast at 20 km/h. Assuming that the temperature drops at a rate of 0.2\(^\circ\)C/km in the northerly direction and 0.3\(^\circ\)C/km in the easterly direction, what is the time rate of change of temperature as observed on the boat?

Question 2.247

Use the chain rule to find a formula for \((d /dt) \,{\exp}\, [f(t) g(t)].\)

Question 2.248

Use the chain rule to find a formula for \((d/ dt) ( f (t)^{g(t)})\).

Question 2.249

Verify the chain rule for the function \(f(x,y,z) = [ \ln\, (1+ x^2 + 2 z^2)] /(1 + y^2)\) and the path \({\bf c} (t) = (t, 1- t^2, \cos t)\).

Question 2.250

Verify the chain rule for the function \(f(x,y) = x^2 / (2 + \cos y)\) and the path \(x = e^t,\) \(y= e^{-t}\).

Question 2.251

Suppose that \(u (x,t)\) satisfies the differential equation \(u_t + uu_x =0\) and that \(x\), as a function \(x= f(t)\) of \(t\), satisfies \(dx/dt = u(x,t)\). Prove that \(u ( f(t),t)\) is constant in \(t\).

Question 2.252

The displacement at time \(t\) and horizontal position on a line \(x\) of a certain violin string is given by \(u = \sin\, ( x- 6t) + \sin\, ( x+ 6t)\). Calculate the velocity of the string at \(x=1\) when \(t = \frac{1}{3}\).

Question 2.253

The ideal gas law \(PV = nRT\) involves a constant \(R\), the number \(n\) of moles of the gas, the volume \(V\), the Kelvin temperature \(T\), and the pressure \(P\).

• (a) Show that each of \(n,P,T,V\) is a function of the remaining variables, and determine explicitly the defining equations.
• (b) Calculate \(\partial V / \partial T, \partial T / \partial P, \partial P / \partial V\) and show that their product equals \(-1\).

Question 2.254

The potential temperature \(\theta\) is defined in terms of temperature \(T\) and pressure \(p\) by \[ \theta = T \left( \frac{1000}{p} \right)^{0.286}. \]

The temperature and pressure may be thought of as functions of position \((x,y,z)\) in the atmosphere and also of time \(t\).

• (a) Find formulas for \(\partial \theta / \partial x, \partial \theta / \partial y, \partial \theta / \partial z, \partial \theta / \partial t\) in terms of partial derivatives of \(T\) and \(p\).
• (b) The condition \(\partial \theta / \partial z < 0\) is regarded as an unstable atmosphere, for it leads to large vertical excursions of air parcels from a single upward or downward impetus. Meteorologists use the formula \[ \frac{\partial \theta}{\partial z}= \frac{\theta}{T} \left( \frac{\partial T}{\partial z} + \frac{g}{C_p} \right), \] where \(g=32.2\) and \(C_p\) is a positive constant. How does the temperature change in the upward direction for an unstable atmosphere?

Question 2.255

The specific volume \(V\), pressure \(P\), and temperature \(T\) of a van der Waals gas are related by \(P = RT / ( V- \beta ) - \alpha / V^2\), where \(\alpha, \beta,\) and \(R\) are constants.

• (a) Explain why any two of \(V,P\), and \(T\) can be considered independent variables that determine the third variable.
• (b) Find \(\partial T / \partial P, \partial P / \partial V, \partial V / \partial T\). Identify which variables are constant, and interpret each partial derivative physically.
• (c) Verify that \(( \partial T / \partial P) ( \partial P / \partial V) ( \partial V / \partial T) = -1 (\hbox{ not } +\! 1!)\).

Question 2.256

The height \(h\) of the Hawaiian volcano Mauna Loa is (roughly) described by the function \(h (x,y) = 2.59 - 0.00024y^2 - 0.00065 x^2\), where \(h\) is the height above sea level in miles and \(x\) and \(y\) measure east–west and north–south distances in miles from the top of the mountain. At \((x,y) = (-2, -4)\):

• (a) How fast is the height increasing in the direction \((1, 1)\) (that is, northeastward)? Express your answer in miles of height per mile of horizontal distance traveled.
• (b) In what direction is the steepest upward path?

Question 2.257

• (a) In what direction is the directional derivative of \(f(x,y) = ( x^2 - y^2)/ (x^2 + y^2)\) at (1, 1) equal to zero?
• (b) How about at an arbitrary point \((x_0, y_0)\) in the first quadrant?
• (c) Describe the level curves of \(f\). In particular, discuss them in terms of the result of part (b).

148

Question 2.258

• (a) Show that the curve \(x^2 -y^2=c\), for any value of \(c\), satisfies the differential equation \(dy/dx = x/y\).
• (b) Draw in a few of the curves \(x^2 - y^2=c\), say for \(c= \pm 1\). At several points \((x,y)\) along each of these curves, draw a short segment of slope \(x/y\); check that these segments appear to be tangent to the curve. What happens when \(y=0\)? What happens when \(c=0\)?

Question 2.259

Suppose that \(f\) is a differentiable function of one variable and that a function \(u = g (x,y)\) is defined by \[ u = g (x,y)= xyf \left( \frac{x+y}{xy} \right). \]

Show that \(u\) satisfies a (partial) differential equation of the form \[ x^2 \frac{ \partial u}{ \partial x} - y^2 \frac{\partial u}{ \partial y}= G (x,y) u \] and find the function \(G (x,y)\).

Question 2.260

• (a) Let \(F\) be a function of one variable and \(f\) a function of two variables. Show that the gradient vector of \(g (x,y) = F (f (x,y))\) is parallel to the gradient vector of \(f(x,y)\).
• (b) Let \(f(x,y)\) and \(g(x,y)\) be functions such that \(\nabla \! f = \lambda\! \nabla \! g\) for some function \(\lambda (x,y)\). What is the relation between the level curves of \(f\) and \(g\)? Explain why there might be a function \(F\) such that \(g (x,y) = F(f(x,y))\).