3.4 Extrema of Real-Valued Functions
Historical Note
As we saw in the book’s Historical Introduction, the early Greeks sought to mathematize nature and to find, as in the geometric Ptolemaic model of planetary motion, mathematical laws governing the universe. With the revival of Greek learning during the Renaissance, this point of view again took hold and the search for these laws recommenced. In particular, the question was raised as to whether there was one law, one mathematical principle that governed and superseded all others, a principle that the Creator used in His Grand Design of the Universe.
MAUPERTUIS’ PRINCIPLE. In 1744, the French scientist Pierre-Louis de Maupertuis (see Figure 3.6) put forth his grand scheme of the world. The “metaphysical principle” of Maupertuis is the assumption that nature always operates with the greatest possible economy. In short, physical laws are a consequence of a principle of “economy of means”; nature always acts in such a way as to minimize some quantity that Maupertuis called the action. Action was nothing more than the expenditure of energy over time, or energy \(\times\) time. In applications, the type of energy changes with each case. For example, physical systems often try to “rearrange themselves” to have a minimum energy—such as a ball rolling from a mountain peak to a valley, or the primordial irregular earth assuming a more nearly spherical shape. As another example, the spherical shape of soap bubbles is connected with the fact that spheres are the surfaces of least area containing a fixed volume.
167

We state Maupertuis’ principle formally as: Nature always minimizes action. Maupertuis saw in this principle an expression of the wisdom of the Supreme Being, of God, according to which everything in nature is performed in the most economical way. He wrote:
What satisfaction for the human spirit that, in contemplating these laws which contain the principle of motion and of rest for all bodies in the universe, he finds the proof of existence of Him who governs the world.
Maupertuis indeed believed that he had discovered God’s fundamental law, the very secret of Creation itself, but he was actually not the first person to pose this principle.
In 1707, Leibniz wrote down the principle of least action in a letter to Johann Bernoulli, which became lost until 1913, when it was discovered in Germany’s Gotha library. For Leibniz, this principle was a natural outgrowth of his great philosophical treatise The Theodicy, in which he argues that God may indeed think of all possible worlds, but would want to create only the best among them; and hence our world is necessarily the best of all possible worlds.
Action, as defined by Leibniz, was motivated by the following reasoning, used in his letter. Think of a hiker walking along a road, and consider how to describe his action. If he travels 2 kilometers in 1 hour, you would say that he has carried out twice as much action as he would if he traveled 2 kilometers in 2 hours. However, you would also say that he carries out twice as much action in traveling 2 kilometers in 2 hours as he would in traveling 1 kilometer in 1 hour. Altogether then, our hiker, by walking 2 kilometers in 1 hour, carries out 4 times as much action as he would in traveling 1 kilometer in 1 hour.
168
Using this intuitive idea, Maupertuis defined action as the product of distance, velocity, and mass: \[ \hbox{Action \({=}\) Mass \(\times\) Distance \(\times\) Velocity.} \]
Mass is included in this definition to account for the hiker’s backpack. Moreover, according to Leibniz, the kinetic energy \(E\) is given by the formula: \[ E = \frac{1}{2}\,{\times}\, \hbox{Mass} \,{\times}\, \hbox{(Velocity)}^{2}. \]
So action has the same physical dimension as \[ \hbox{Energy \(\times\) Time,} \] because velocity is distance divided by time.
In the 250 years after Maupertuis formulated his principle, this principle of least action has been found to be a “theoretical basis” for Newton’s law of gravity, Maxwell’s equations for electromagnetism, Schrödinger’s equation of quantum mechanics, and Einstein’s field equation in general relativity.
There is much more to the story of the least-action principle, which we will revisit in Section 4.1 and in the Internet supplement.
Maxima and Minima for Functions of \(n\)-Variables
As the previous remarks show, for Leibniz, Euler, and Maupertuis, and for much of modern science as well, all in nature is a consequence of some maximum or minimum principle. To make such grand schemes—as well as some that are more down to earth—effective, we must first learn the techniques of how to find maxima and minima of functions of \(n\) variables.
Extreme Points
Among the most basic geometric features of the graph of a function are its extreme points, at which the function attains its greatest and least values. In this section, we derive a method for determining these points. In fact, the method locates local extrema as well. These are points at which the function attains a maximum or minimum value relative only to nearby points. Let us begin by defining our terms.
Definition
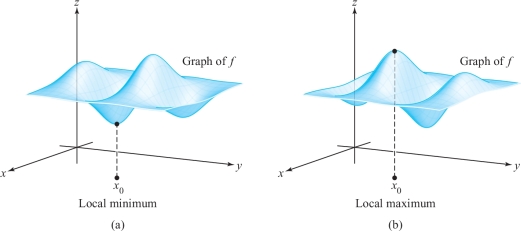
If \(f{:}\,\, U \subset {\mathbb R}^n \to {\mathbb R}\) is a given scalar function, a point \({\bf x}_0 \in U\) is called a local minimum of \(f\) if there is a neighborhood \(V\) of \({\bf x}_0\) such that for all points \({\bf x}\) in \(V\), \(f({\bf x}) \ge f({\bf x}_0)\). \((\)See Figure \(3.3.2.)\) Similarly, \({\bf x}_0 \in U\) is a local maximum if there is a neighborhood \(V\) of \({\bf x}_0\) such that \(f({\bf x}) \le f({\bf x}_0)\) for all \({\bf x}\in V\). The point \({\bf x}_0 \in U\) is said to be a local, or relative, extremum if it is either a local minimum or a local maximum. A point \({\bf x}_0\) is a critical point of \(f\) if either \(f\) is not differentiable at \({\bf x}_0\), or if it is, \(\,{\bf D}\!f({\bf x}_0) = {\bf 0}\). A critical point that is not a local extremum is called a saddle point.footnote #
First-Derivative Test for Local Extrema
169
The location of extrema is based on the following fact, which should be familiar from one-variable calculus (the case \(n = 1\)): Every extremum is a critical point.
Theorem 4 First-Derivative Test for Local Extrema
If \(\,U \subset {\mathbb R}^n\) is open, the function \(f{:}\,\, U \subset {\mathbb R}^n \to {\mathbb R}\) is differentiable, and \({\bf x}_0 \in U\) is a local extremum, then \({\bf D}\! f({\bf x}_0) ={\bf 0};\) that is, \({\bf x}_0\) is a critical point of \(f\).
proof
Suppose that \(f\) achieves a local maximum at \({\bf x}_{\bf 0}\). Then for any \({\bf h}\in {\mathbb R}^n\), the function \(g(t) = f({\bf x}_0 + t{\bf h})\) has a local maximum at \(t=0\). Thus, from one- variable calculus \(g'(0) = 0\).footnote # On the other hand, by the chain rule, \[ g'(0) = [{\bf D}\! f({\bf x}_0)]{\bf h}. \]
Thus, \([{\bf D}\! f({\bf x}_0)]{\bf h} = 0\) for every \({\bf h}\), and so \({\bf D}\! f({\bf x}_0) ={\bf 0}\). The case in which \(f\) achieves a local minimum at \({\bf x}_0\) is entirely analogous.
If we remember that \({\bf D}\! f({\bf x}_0) = {\bf 0}\) means that all the components of \({\bf D}\! f({\bf x}_0)\) are zero, we can rephrase the result of Theorem 4: If \({\bf x}_0\) is a local extremum, then \[ \frac{\partial f}{\partial x_i} ({\bf x}_0) =0,\qquad i = 1, \ldots , n; \] that is, each partial derivative is zero at \({\bf x}_0\). In other words, \(\nabla\! f({\bf x}_0) ={\bf 0}\), where \(\nabla \! f\) is the gradient of \(f\).
If we seek to find the extrema or local extrema of a function, then Theorem 4 states that we should look among the critical points. Sometimes these can be tested by inspection, but usually we use tests (to be developed below) analogous to the second-derivative test in one-variable calculus.
170
example 1
Find the maxima and minima of the function \(f{:}\,\, {\mathbb R}^2 \to {\mathbb R}\), defined by \(f(x,y) = x^2 + y^2\). (Ignore the fact that this example can be done by inspection.)
solution We first identify the critical points of \(f\) by solving the two equations \(\partial f/\partial x=0\) and \(\partial f/\partial y=0\), for \(x\) and \(y\). But \[ \frac{\partial f}{\partial x} = 2x \qquad \hbox{and} \qquad \frac{\partial f}{\partial y} = 2y, \] so the only critical point is the origin (0, 0), where the value of the function is zero. Because \(f(x,y) \ge 0\), this point is a relative minimum—in fact, an absolute, or global, minimum—of \(f\). Because (0, 0) is the only critical point, there are no maxima.
example 2
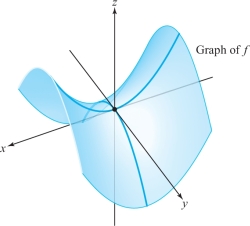
Consider the function \(f{:}\,\,{\mathbb R}^2 \to {\mathbb R}, (x,y) \mapsto x^2 - y^2\). Ignoring for the moment that this function has a saddle and no extrema, apply the method of Theorem 4 for the location of extrema.
solution As in Example 1, we find that \(f\) has only one critical point, at the origin, and the value of \(f\) there is zero. Examining values of \(f\) directly for points near the origin, we see that \(f(x,0) \ge f(0,0)\) and \(f(0,y) \le f(0,0)\), with strict inequalities when \(x \neq 0\) and \(y \neq 0\). Because \(x\) or \(y\) can be taken arbitrarily small, the origin cannot be either a relative minimum or a relative maximum (so it is a saddle point). Therefore, this function can have no relative extrema (see Figure 3.8).
example 3
Find all the critical points of \(z = x^2y + y^2 x\).
solution Differentiating, we obtain \[ \frac{\partial z}{\partial x} = 2xy + y^2, \qquad \frac{\partial z}{\partial y} = 2xy + x^2. \] Equating the partial derivatives to zero yields \[ 2xy + y^2 = 0,\qquad 2xy + x^2 =0. \]
171
Subtracting, we obtain \(x^2 = y^2\). Thus, \(x = \pm y\). Substituting \(x = +y\) in the first of the two preceding equations, we find that \[ 2y^2 + y^2 = 3y^2 = 0, \] so that \(y = 0\) and thus \(x = 0\). If \(x = -y\), then \[ -2y^2 + y^2 = -y^2 = 0, \] so \(y = 0\) and therefore \(x=0\). Hence, the only critical point is \((0,0)\). For \(x=y\), \(z= 2x^3\), which is both positive and negative for \(x\) near zero. Thus, \((0, 0)\) is not a relative extremum.
example 4
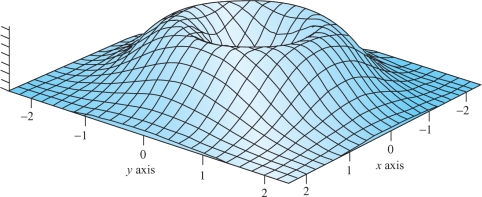
Refer to Figure 3.9, a computer-drawn graph of the function \(z=2(x^2+y^2)\) \(e^{-x^2-y^2}\). Where are the critical points?
solution Because \(z=2(x^2+y^2)e^{-x^2-y^2}\), we have \begin{eqnarray*} \frac{\partial z}{\partial x}&=&4x(e^{-x^2-y^2})+2(x^2+y^2)e^{-x^2-y^2}(-2x)\\[4pt] &=& e^{-x^2-y^2}[4x-4x(x^2+y^2)]\\[4pt] &=& 4x(e^{-x^2-y^2})(1-x^2-y^2) \end{eqnarray*} and \[ \frac{\partial z}{\partial y}=4y(e^{-x^2-y^2}) (1-x^2-y^2). \]
These both vanish when \(x=y=0\) or when \(x^2+y^2=1\). This is consistent with the figure: Points on the crater’s rim are maxima and the origin is a minimum.
Second-Derivative Test for Local Extrema
The remainder of this section is devoted to deriving a criterion, depending on the second derivative, for a critical point to be a relative extremum. In the special case \(n = 1\), our criterion will reduce to the familiar condition from one-variable calculus: \(f''(x_0) > 0\) for a minimum and \(f''(x_0) < 0\) for a maximum. But in the general context, the second derivative is a fairly complicated mathematical object. To state our criterion, we will introduce a version of the second derivative called the Hessian, which in turn is related to quadratic functions. Quadratic functions are functions \(g{:}\,\,{\mathbb R}^n \to {\mathbb R}\) that have the form \[ g(h_1, \ldots , h_n) = \sum_{i,j=1}^n a_{\it ij}h_ih_j \] for an \(n\times n\) matrix \([a_{\it ij}]\). In terms of matrix multiplication, we can write \[ g(h_1, \ldots , h_n) = [h_1 \cdots h_n] \left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} a_{11} &a_{12} &\cdots & a_{1n}\\[2pt] \vdots &\vdots & & \vdots\\[2pt] a_{n1} &a_{n2} &\cdots & a_{nn} \end{array}\right] \left[\begin{array}{c} h_1\\[3pt] \vdots\\[3pt] h_n \end{array}\right]\!. \]
172
For example, if \(n=3\), \[ g(h_1,h_2,h_3) = h^2_1- 2h_1h_2+ h^2_3=[h_1\, h_2\, h_3] \left[\begin{array}{r@{\quad}r@{\quad}r} 1 & -1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 1 \\ \end{array}\right]\left[ \begin{array}{c} h_1\\[1pt] h_2\\[1pt] h_3 \end{array}\right] \] is a quadratic function.
We can, if we wish, assume that \([a_{\it ij}]\) is symmetric; in fact, \(g\) is unchanged if we replace \([a_{\it ij}]\) by the symmetric matrix \([b_{\it ij}]\), where \(b_{\it ij} = \frac12 (a_{\it ij}+a_{ji})\), because \(h_ih_j = h_jh_i\) and the sum is over all \(i\) and \(j\). The quadratic nature of \(g\) is reflected in the identity \[ g(\lambda h_1,\ldots, \lambda h_n) = \lambda^2g(h_1, \ldots, h_n), \] which follows from the definition.
Now we are ready to define Hessian functions (named after Ludwig Otto Hesse, who introduced them in 1844).
Definition
Suppose that \(f{:}\,\, U \,{\subset}\, {\mathbb R}^n \,{\to}\, {\mathbb R}\) has second-order continuous deriva- tives \((\partial^2\! f/\) \(\partial x_i\, \partial x_j)({\bf x}_0),\) for \(i,j=1,\ldots, n,\) at a point \({\bf x}_0 \in U\). The Hessian of f at \({\bf x}_0\)} is the quadratic function defined by \begin{eqnarray*} {\it Hf}({\bf x}_0)({\bf h}) &=& \frac{1}{2} \sum_{i,j=1}^n \frac{\partial^2\!f}{\partial x_i\, \partial x_j} ({\bf x}_0) h_ih_j\\ &=& \frac{1}{2}[h_1,\ldots,h_n]\left[ \begin{array}{c@{\quad}c@{\quad}c} \displaystyle\frac{\partial^2{f}}{\partial x_1\,\partial x_1} & \cdots& \displaystyle\frac{\partial^2{f}}{\partial x_1\,\partial x_n}\\ \vdots\\[3pt] \displaystyle\frac{\partial^2{f}}{\partial x_n\,\partial x_1} & \cdots& \displaystyle\frac{\partial^2{f}}{\partial x_n\,\partial x_n}\\[7pt] \end{array}\right]\left[ \begin{array}{c} h_1\\ \vdots\\[2pt] h_n \end{array}\right].\\[-11pt] \end{eqnarray*}
Notice that, by equality of mixed partials, the second-derivative matrix is symmetric.
173
This function is usually used at critical points \({\bf x}_0 \in U\). In this case, \({\bf D}\! f({\bf x}_0) = {\bf 0}\), so the Taylor formula (see Theorem 2, Section 3.3) may be written in the form \[ f({\bf x}_0 + {\bf h}) = f({\bf x}_0) + {\it Hf} ({\bf x}_0)({\bf h}) + R_2({\bf x}_0, {\bf h}). \]
Thus, at a critical point the Hessian equals the first nonconstant term in the Taylor series of \(f\).
A quadratic function \(g{:}\,\, {\mathbb R}^n \to {\mathbb R}\) is called positive-definite if \(g({\bf h}) \ge 0\) for all \({\bf h}\in {\mathbb R}^n\) and \(g({\bf h})=0\) only for \({\bf h} = {\bf 0}\). Similarly, \(g\) is negative-definite if \(g({\bf h})\le 0\) and \(g({\bf h}) = 0\) for \({\bf h} = {\bf 0}\) only.
Note that if \(n = 1\), \({\it Hf}(x_0)(h) = \frac{1}{2} f”(x_0) h^2\), which is positive-definite if and only if \(f''(x_0) > 0\).
Theorem 5 Second-Derivative Test for Local Extrema
If \(f{:}\,\, U \subset {\mathbb R}^n \to {\mathbb R}\) is of class \(C^3,\) \({\bf x}_0 \in U\) is a critical point of \(f,\) and the Hessian \({\it Hf}({\bf x}_0)\) is positive-definite, then \({\bf x}_0\) is a relative minimum of \(f\). Similarly, if \({\it Hf}({\bf x}_0)\) is negative-definite, then \({\bf x}_0\) is a relative maximum.
Actually, we shall prove that the extrema given by this criterion are strict. A relative maximum \({\bf x}_0\) is said to be strict if \(f({\bf x})< f({\bf x}_0)\) for nearby \({\bf x}\neq {\bf x}_0\). A strict relative minimum is defined similarly. Also, the theorem is valid even if \(f\) is only \(C^2\), but we have assumed \(C^3\) for simplicity.
The proof of Theorem 5 requires Taylor’s theorem and the following result from linear algebra.
Lemma 1
If \(B=[b_{\it ij}]\) is an \(n \times n\) real matrix, and if the associated quadratic function \[ H{:}\,\, {\mathbb R}^n \to {\mathbb R}, (h_1,\ldots, h_n) \mapsto \frac12 \sum_{i,j=1}^n b_{\it ij}h_ih_j \] is positive-definite, then there is a constant \(M > 0\) such that for all \({\bf h}\in {\mathbb R}^n\); \[ H({\bf h}) \ge M \|{\bf h}\|^2. \]
proof
For \(\|{\bf h}\|=1\), set \(g({\bf h})= H({\bf h})\). Then \(g\) is a continuous function of \({\bf h}\) for \(\|{\bf h}\| = 1\) and so achieves a minimum value, say \(M\).footnote # Because \(H\) is quadratic, we have \[ H({\bf h}) = H \bigg(\frac{\bf h}{\|{\bf h}\|} \|{\bf h}\|\bigg) =H \bigg(\frac{\bf h}{\|{\bf h}\|}\bigg)\|{\bf h}\|^2 = g \bigg(\frac{\bf h}{\|{\bf h}\|}\bigg)\|{\bf h}\|^2 \ge M\|{\bf h}\|^2 \] for any \({\bf h}\neq {\bf 0}\). (The result is obviously valid if \({\bf h}={\bf 0}\).)
Note that the quadratic function associated with the symmetric matrix \(\frac12(\partial^2 \!f /\partial x_i\,\partial x_j)\) is exactly the Hessian.
174
proof of theorem 5
Recall that if \(f{:}\, \,U\subset {\mathbb R}^n \to {\mathbb R}\) is of class \(C^3\) and \({\bf x}_0 \in U\) is a critical point, Taylor’s theorem may be expressed in the form \[ f({\bf x}_0 + {\bf h}) - f({\bf x}_0) = {\it Hf}({\bf x}_0) ({\bf h}) + R_2({\bf x}_0, {\bf h}), \] where \(({R_2({\bf x}_0, {\bf h}))}/{\|{\bf h}\|^2} \to 0 \hbox{ as } {\bf h}\to {\bf 0}\).
Because \({\it Hf}({\bf x}_0)\) is positive-definite, Lemma 1 assures us of a constant \(M > 0\) such that for all \({\bf h}\in {\mathbb R}^n\) \[ {\it Hf}({\bf x}_0) ({\bf h}) \ge M\|{\bf h}\|^2. \]
Because \(R_2({\bf x}_0, {\bf h})/\|{\bf h}\|^2\to 0\) as \({\bf h}\to {\bf 0}\), there is a \(\delta > 0\) such that for \(0 < \|{\bf h}\| < \delta\) \[ | R_2({\bf x}_0,{\bf h})| < M \|{\bf h}\|^2. \]
Thus, \(0 < {\it Hf}({\bf x}_0)({\bf h }) + \boldsymbol{\mathit{R}}_2({\bf x}_0,{\bf h}) = f({\bf x}_0 + {\bf h} )- f({\bf x}_0 )\) for \(0 < \|{\bf h}\| < \delta\), so that \({\bf x}_0\) is a relative minimum; in fact, a strict relative minimum.
The proof in the negative-definite case is similar, or else follows by applying the preceding to \(-f\), and is left as an exercise.
example 5
Consider again the function \(f{:}\,\, {\mathbb R}^2 \to {\mathbb R}, (x,y) \mapsto x^2 + y^2\). Then \((0, 0)\) is a critical point, and \(f\) is already in the form of Taylor’s theorem\(:\) \[ f((0,0) + (h_1, h_2)) = f(0,0) + (h_1^2 + h_2^2) + 0. \]
We can see directly that the Hessian at \((0, 0)\) is \[ {\it Hf}({\bf 0})({\bf h}) = h_1^2 + h_2^2, \] which is clearly positive-definite. Thus, \((0, 0)\) is a relative minimum. This simple case can, of course, be done without calculus. Indeed, it is clear that \(f(x,y) > 0\) for all \((x,y)\neq (0,0)\).
For functions of two variables \(f(x,y)\), the Hessian may be written as follows: \[ {\it Hf}(x,y)({\bf h}) = {\textstyle\frac{1}{2}}[h_1,h_2] \left[\begin{array}{c@{\quad}c} \displaystyle\frac{\partial^2\!f}{\partial x^2} & \displaystyle\frac{\partial^2\! f}{\partial y\,\partial x}\\[12pt] \displaystyle \frac{\partial^2\! f}{\partial x\,\partial y} & \displaystyle\frac{\partial^2\! f}{\partial y^2} \end{array}\right] \left[\begin{array}{c} h_1\\[3pt] h_2 \end{array}\right]\!. \]
Now we shall give a useful criterion for when a quadratic function defined by such a \(2\times 2\) matrix is positive-definite. This will be useful in conjunction with Theorem 5.
Lemma 2
Let \[ B= \left[\begin{array}{c@{\quad}c} a & b\\ b & c \end{array}\right]\qquad \hbox{and }\qquad H({\bf h}) = {\textstyle\frac{1}{2}}[h_1,h_2]B \left[\begin{array}{c} h_1\\[3pt] h_2 \end{array}\right]\!. \]
Then \(H({\bf h})\) is positive-definite if and only if \(a > 0\) and det \(B = ac - b^2 >0\).
175
proof
We have \[ H({\bf h}) = {\textstyle\frac{1}{2}}[h_1,h_2] \left[\begin{array}{c} ah_1 + bh_2\\[3pt] bh_1 + ch_2 \end{array}\right] = {\textstyle\frac{1}{2}} (ah_1^2 + 2bh_1h_2 + ch_2^2). \]
Let us complete the square, writing \[ H({\bf h}) = {\frac12} a\bigg(h_1 + \frac{b}{a}h_2\bigg)^2 + {\frac12} \bigg(c- \frac{b^2}{a}\bigg) h_2^2. \]
Suppose \(H\) is positive-definite. Setting \(h_2 \,{=}\, 0\), we see that \(a\,{>}\,0\). Setting \(h_1 \,{=}{-}(b/a)h_2\), we get \(c\,{-}\,b^2/a\,{>}\,0\) or \(ac\,{-}\,b^2 \,{>}\, 0\). Conversely, if \(a\,{>}\,0\) and \(c\,{-}\,b^2/a>0\), \(H({\bf h})\) is a sum of squares, so that \(H({\bf h}) \ge 0\). If \(H({\bf h}) =0\), then each square must be zero. This implies that both \(h_1\) and \(h_2\) must be zero, so that \(H({\bf h})\) is positive-definite.
Similarly, we can see that \(H({\bf h})\) is negative-definite if and only if \(a \,{<}\, 0\) and \(ac \,{-}\, b^2 \,{>}\, 0\). We note that an alternative formulation is that \(H({\bf h})\) is positive-(respectively, negative-) definite if \(a+c=\) trace \(B>0\) (respectively, \(< 0\)) and det \(B>0\).
Determinant Test for Positive Definiteness
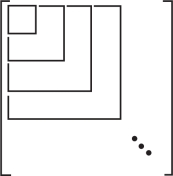
There are similar criteria to test the positive (or negative) definiteness of an \(n \times n\) symmetric matrix \(B\), thus providing a maxima and minima test for functions of \(n\)-variables. Consider the \(n\) square submatrices along the diagonal (see Figure 3.10). \(B\) is positive-definite (that is, the quadratic function associated with \(B\) is positive-definite) if and only if the determinants of these diagonal submatrices are all greater than zero. For negative-definite \(B\), the signs should be alternately \({<\!0}\) and \({>\!0}\). We shall not prove this general case here.footnote # In case the determinants of the diagonal submatrices are all nonzero, but the Hessian matrix is not positive- or negative-definite, the critical point is of saddle type; in this case, we can show that the point is neither a maximum nor a minimum in the manner of Example 2.
General Second-Derivative Tests (\(n\)-variables)
176
Suppose \({\bf x}_{0} \in \mathbb{R}^n\) is a critical point for a \(C^2\) function \(f: U \to \mathbb{R},\) \(U\) an open set containing \({\bf x}_{0}\); that is, \(\frac{\partial f}{\partial x_i} ({\bf x}_{0})=0,\) \(i=1,\cdots,n.\) Suppose that the Hessian matrix \(\{\frac{\partial^2f}{\partial x_i \partial x_j} ({\bf x}_{0})\}\) is positive-definite; then \({\bf x}_{0}\) is a strict local minimum for \(f\). If the Hessian matrix is negative-definite, \({\bf x}_{0}\) is a strict local maximum. If the Hessian matrix is neither positive- nor negative-definite, but its determinant is nonzero, it is of saddle type (it is neither a maximum nor a minimum). If the determinant of the Hessian is zero, it is said to be of degenerate type and nothing can be said about the nature of the critical point without further analysis. Figure 3.10 illustrates a simple test for the positive definiteness of a symmetric matrix. In the case of two variables, the maximum and minimum test can be considerably simplified.
Second-Derivative Test (two variables)
Lemma 2 and Theorem 5 imply the following result:
Theorem 6 Second-Derivative Maximum-Minimum Test for Functions of Two Variables
Let \(f(x,y)\) be of class \(C^2\) on an open set \(U\) in \({\mathbb R}^2\). A point \((x_0,y_0)\) is a \((\)strict\()\) local minimum of \(f\) provided the following three conditions hold:
- (i) \(\displaystyle \frac{\partial f}{\partial x}(x_0,y_0) = \frac{\partial f}{\partial y} (x_0,y_0) = 0\)
- (ii) \(\displaystyle \frac{\partial^2\! f}{\partial x^2}(x_0,y_0) >0\)
- (iii) \(\displaystyle D= \bigg(\frac{\partial^2\! f}{\partial x^2}\bigg) \bigg(\frac{\partial^2\! f}{\partial y^2}\bigg)- \bigg(\frac{\partial^2\! f}{\partial x\,\partial y}\bigg)^2 > 0\ {\rm at}\ (x_0,y_0)\) \((D\) is called the discriminant of the Hessian.) If in (ii) we have \({<\! 0}\) instead of \({>\!0}\) and condition (iii) is unchanged, then we have a (strict) local maximum. If \(D<0\) (e.g., if \(\displaystyle\frac{\partial^2f}{\partial x^2}(x_0,y_0)=0\) or \(\displaystyle\frac{\partial^2\! f}{\partial y^2}(x_0,y_0)=0\), but \(\displaystyle\frac{\partial^2\! f}{\partial x \partial y}(x_0,y_0) \neq 0\)), then \((x_0,y_0)\) is of saddle type (neither a maximum nor a minimum).
example 6
Classify the critical points of the function \(f{:}\,\, {\mathbb R}^2 \to {\mathbb R}\), defined by \((x,y) \mapsto x^2 - 2xy + 2y^2\).
solution As in Example 5, we find that \(f(0,0)=0\), the origin is the only critical point, and the Hessian is \[ {\it Hf}({\bf 0})({\bf h}) = h_1^2 - 2h_1 h_2 + 2h_2^2 = (h_1 - h_2)^2 + h_2^2, \] which is clearly positive-definite. Thus, \(f\) has a relative minimum at \((0, 0)\). Alternatively, we can apply Theorem 6. At \((0, 0)\), \(\partial^2 \!f /\partial x^2 = 2, \partial^2\! f/\partial y^2 = 4\), and \(\partial^2\! f/\partial x\, \partial y=-2\). Conditions (i), (ii), and (iii) hold, so \(f\) has a relative minimum at \((0, 0)\).
177
If \(D<0\) in Theorem 6, then we have a saddle point. In fact, we can prove that \(f(x,y)\) is larger than \(f(x_0,y_0)\) as we move away from \((x_0,y_0)\) in some direction and smaller in the orthogonal direction (see Exercise 32). The general appearance is thus similar to that shown in Figure 3.8. The appearance of the graph near \((x_0,y_0)\) in the case \(D=0\) must be determined by further analysis.
We summarize the procedure for dealing with functions of two variables: After all critical points have been found and their associated Hessians computed, some of these Hessians may be positive-definite, indicating relative minima; some may be negative-definite, indicating relative maxima; and some may be neither positive- nor negative-definite, indicating saddle points. The shape of the graph at a saddle point where \(D< 0\) is like that in Figure 3.8. Critical points for which \(D\neq 0\) are called nondegenerate critical points. Such points are maxima, minima, or saddle points. The remaining critical points, where \(D=0\), may be tested directly, with level sets and sections or by some other method. Such critical points are said to be degenerate; the methods developed in this chapter fail to provide a picture of the behavior of a function near such points, so we examine them case by case.
example 7
Locate the relative maxima, minima, and saddle points of the function \[ f(x,y) = \log\, (x^2 + y^2 +1). \]
solution We must first locate the critical points of this function; therefore, according to Theorem 3, we calculate \[ \nabla\! f(x,y) = \frac{2x}{x^2 + y^2 + 1}\, \,{\bf i} + \frac{2y}{x^2 + y^2 + 1}\,{\bf j}. \]
Thus, \(\nabla\! f(x,y) ={\bf 0}\) if and only if \((x,y) = (0,0)\), and so the only critical point of \(f\) is \((0, 0)\). Now we must determine whether this is a maximum, a minimum, or a saddle point. The second partial derivatives are \begin{eqnarray*} \frac{\partial^2\! \! f}{\partial x^2} &=& \frac{2(x^2 +y^2 +1) -(2x)(2x)}{(x^2 + y^2 +1)^2},\\[5pt] \frac{\partial^2\!\! f}{\partial y^2} &=& \frac{2(x^2 +y^2 +1) -(2y)(2y)}{(x^2 + y^2 +1)^2}, \end{eqnarray*} and \[ \frac{\partial^2\! f}{\partial x\,\partial y} = \frac{-2x(2y)}{(x^2 + y^2 + 1)^2}. \]
Therefore, \[ \frac{\partial^2\! f}{\partial x^2} (0,0) =2 =\frac{\partial^2\! f}{\partial y^2}(0,0) \qquad \hbox{and}\qquad \frac{\partial^2\!f}{\partial x\, \partial y} (0,0) =0, \] which yields \[ D = 2 \,{\cdot}\, 2 = 4 >0. \]
Because \((\partial^2\! f/\partial x^2)(0,0) > 0\), we conclude by Theorem 6 that \((0, 0)\) is a local minimum. (Can you show this just from the fact that log \(t\) is an increasing function of \(t > 0?\))
178
example 8
The graph of the function \(g(x,y) = 1/xy\) is a surface \(S\) in \({\mathbb R}^3\). Find the points on \(S\) that are closest to the origin \((0, 0, 0)\). (See Figure 3.11.)
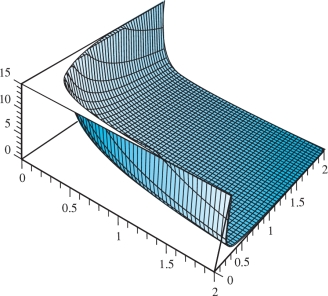
solution Each point on \(S\) is of the form \((x,y,1/xy)\). The distance from this point to the origin is \[ d(x,y)=\sqrt{x^2+y^2+\frac{1}{x^2y^2}}. \]
It is easier to work with the square of \(d\), so let \(f(x,y)=x^2+y^2+(1/x^2y^2)\), which will have the same minimum point. This follows from the fact that \(d(x,y)^2 \geq d(x_0,y_0)^2\) if and only if \(d(x,y) \geq d(x_0,y_0)\). Notice that \(f(x,y)\) becomes very large as \(x\) and \(y\) get larger and larger; \(f(x,y)\) also becomes very large as \((x, y)\) approaches the \(x\) or \(y\) axis where \(f\) is not defined, so \(f\) must attain a minimum at some critical point. The critical points are determined by: \begin{eqnarray*} \frac{\partial f}{\partial x} &=& 2x-\frac{2}{x^3y^2}=0,\\[2pt] \frac{\partial f}{\partial y} &=& 2y-\frac{2}{y^3x^2}=0, \end{eqnarray*} that is, \(x^4y^2-1=0\), and \(x^2y^4-1=0\). From the first equation we get \(y^2=1/x^4\), and, substituting this into the second equation, we obtain \[ \frac{x^2}{x^8}=1=\frac{1}{x^6}. \]
Thus, \(x=\pm 1\) and \(y=\pm 1\), and it therefore follows that \(f\) has four critical points, namely, (1, 1), \((1,-1),(-1,1)\), and \((-1,-1)\). Note that \(f\) has the value 3 for all these points, so they are all minima. Therefore, the points on the surface closest to the point (0, 0, 0) are (1, 1, 1), \((1,-1,-1),(-1,1,-1)\), and \((-1,-1,1)\) and the minimum distance is \(\sqrt{3}\). Is this consistent with the graph in Figure 3.11?
179
example 9
Analyze the behavior of \(z = x^5y + xy^5 +xy\) at its critical points.
solution The first partial derivatives are \[ \frac{\partial z}{\partial x} = 5x^4y + y^5 + y = y(5x^4 +y^4 +1) \] and \[ \frac{\partial z}{\partial y} = x(5y^4 + x^4 + 1). \]
The terms \(5x^4 + y^4 +1\) and \(5y^4 + x^4 +1\) are always greater than or equal to 1, and so it follows that the only critical point is \((0, 0)\).
The second partial derivatives are \[ \frac{\partial^2z}{\partial x^2} = 20x^3 y, \qquad \frac{\partial^2z}{\partial y^2} = 20x y^3 \] and \[ \frac{\partial^2z}{\partial x\,\partial y} =5x^4 + 5y^4 +1. \]
Thus, at \((0,0), D=-1\), and so \((0, 0)\) is a nondegenerate saddle point and the graph of \(z\) near \((0, 0)\) looks like the graph in Figure 3.8.
We now look at an example for a function of three variables.
example 10
Consider \(f(x,y)=x^2+y^2+z^2+2xyz\). Show that \((0,0,0)\) and \((-1,1,1)\) are both critical points. Determine whether they are local minima, local maxima, saddle points, or none of them.
solution \(\frac{\partial f}{\partial x} = 2x+2yz\), \(\frac{\partial f}{\partial y} = 2y+2xz\), and \(\frac{\partial f}{\partial z} = 2z+2xy\), all of which vanish at \((0,0,0)\) and \((-1,1,1)\). Thus, these are critical points. The Hessian of \(f\) at \((0,0,0)\) is \[ \left[ \begin{array}{c@{\quad}c@{\quad}c} 2 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 2 \end{array}\right]. \]
The diagonal submatrices are \([2]\) and \(\left[ \begin{array}{c@{\quad}c} 2 & 0\\ 0 & 2 \end{array}\right]\) and the Hessian itself, all of which have positive determinants. Therefore (c.f. Figure 3.10) \((0,0,0)\) is a strict local minimum. On the other hand, the Hessian matrix of \(f\) at \((-1,1,1)\) is \[ \left[ \begin{array}{c@{\quad}c@{\quad}c} \displaystyle\frac{\partial ^2 \! f}{\partial x^2} & \displaystyle\frac{\partial ^2 \! f}{\partial x \partial y} & \displaystyle\frac{\partial ^2 \! f}{\partial x \partial z}\\[9pt] \displaystyle\frac{\partial ^2 \! f}{\partial y \partial x} &\displaystyle\frac{\partial ^2 \! f}{\partial y^2} & \displaystyle\frac{\partial ^2 \! f}{\partial y \partial z}\\[9pt] \displaystyle\frac{\partial ^2 \! f}{\partial z \partial x} & \displaystyle\frac{\partial ^2 \! f}{\partial z \partial y} & \displaystyle\frac{\partial ^2 \! f}{\partial z^2} \end{array}\right] \] or \[ \left[ \begin{array}{c@{\quad}r@{\quad}r} 2 & 2 & 2\\ 2 & 2 & -2\\ 2 & -2 & 2 \end{array}\right]. \]
180
The determinant of the first diagonal matrix is \(2\), the second diagonal matrix \[ \left[ \begin{array}{c@{\quad}c} 2 & 2\\ 2 & 2\\ \end{array}\right] \] is zero, and the determinant of the Hessian is \(-16\). Thus, the critical point \((-1,1,1)\) is of saddle type (i.e., neither a maximum nor a minimum).
Global Maxima and Minima
We end this section with a discussion of the theory of absolute, or global, maxima and minima of functions of several variables. Unfortunately, the location of absolute maxima and minima for functions on \({\mathbb R}^n\) is, in general, a more difficult problem than for functions of one variable.
Definition
Suppose \(f{:}\,\, A\to {\mathbb R}\) is a function defined on a set \(A\) in \({\mathbb R}^2\) or \({\mathbb R}^3\). A point \({\bf x}_0 \in A\) is said to be an absolute maximum \((\)or absolute minimum\()\) point of \(f\) if \(f({\bf x}) \le f({\bf x}_0)\) [or \(f({\bf x}) \ge f({\bf x}_0)]\) for all \({\bf x} \in A\).
In one-variable calculus, we learn—but often do not prove—that every continuous function on a closed interval \(I\) assumes its absolute maximum (or minimum) value at some point \({\bf x}_0\) in \(I\). A generalization of this theoretical fact also holds in \({\mathbb R}^n\). Such theorems guarantee that the maxima or minima one is seeking actually exist; therefore, the search for them is not in vain.
Definition
A set \(D \in {\mathbb R}^n\) is said to be bounded if there is a number \(M>0\) such that \(\|{\bf x}\| < M\) for all \({\bf x}\in D\). A set is closed if it contains all its boundary points.
As an important example, we note that the level sets \(\{(x_1,x_2,\cdots,x_n)\, | f(x_1, x_2,\ldots, x_n)=c\}\) of a continuous function \(f\) are always closed.
Thus, a set is bounded if it can be strictly contained in some (large) ball. The appropriate generalization of the one-variable theorem on maxima and minima is the following result, stated without proof.
Theorem 7 Global Existence Theorem for Maxima and Minima
Let \(D\) be closed and bounded in \({\mathbb R}^n\) and let \(f{:}\,\, D\to {\mathbb R}\) be continuous. Then \(f\) assumes its absolute maximum and minimum values at some points \({\bf x}_0\) and \({\bf x}_1\) of \(D\).
181
Simply stated, \({\bf x}_0\) and \({\bf x}_1\) are points where \(f\) assumes its largest and smallest values. As in one-variable calculus, these points need not be uniquely determined.
Suppose now that \(D=U\cup \partial U\), where \(U\) is open and \(\partial U\) is its boundary. If \(D\subset {\mathbb R}^2\), we suppose that \(\partial U\) is a piecewise smooth curve; that is, \(D\) is a region bounded by a collection of smooth curves—for example, a square or the sets depicted in Figure 3.12.
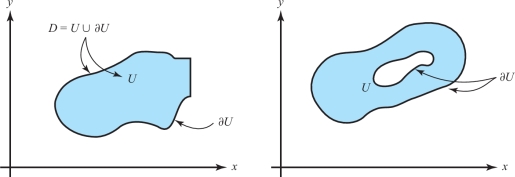
If \({\bf x}_0\) and \({\bf x}_1\) are in \(U\), we know from Theorem 4 that they are critical points of \(f\). If they are in \(\partial U\), and \(\partial U\) is a smooth curve (i.e., the image of a smooth path \({\bf c}\) with \({\bf c}'\neq 0\)), then they are maximum or minimum points of \(f\) viewed as a function on \(\partial U\). These observations provide a method of finding the absolute maximum and minimum values of \(f\) on a region \(D\).
Strategy for Finding the Absolute Maxima and Minima on a Region with Boundary
Let \(f\) be a continuous function of two variables defined on a closed and bounded region \(D\) in \({\mathbb R}^2\), which is bounded by a smooth closed curve. To find the absolute maximum and minimum of \(f\) on \(D\):
- (i) Locate all critical points for \(f\) in \(U\).
- (ii) Find all the critical points of \(f\) viewed as a function only on \(\partial U\).
- (iii) Compute the value of \(f\) at all of these critical points.
- (iv) Compare all these values and select the largest and the smallest.
If \(D\) is a region bounded by a collection of smooth curves (such as a square), then we follow a similar procedure, but including in step (iii) the points where the curves meet (such as the corners of the square).
All the steps except step (ii) should now be familiar to you. To carry out step (ii) in the plane, one way is to find a smooth parametrization of \(\partial U\); that is, we find a path \({\bf c}{:}\, I \to \partial U\), where \( I\) is some interval, which is onto \(\partial U\). Second, we consider the function of one variable \(t \mapsto f({\bf c}(t)),\) where \(t \in I\), and locate the maximum and minimum points \(t_0, t_1 \in I\) (remember to check the endpoints!). Then \({\bf c}(t_0), {\bf c}(t_1)\) will be maximum and minimum points for \(f\) as a function on \(\partial U\). Another method for dealing with step (ii) is the Lagrange multiplier method, to be presented in the next section.
182
example 11
Find the maximum and minimum values of the function \(f(x,y)=x^2+y^2 -x -y +1\) in the disc \(D\) defined by \(x^2 + y^2 \le 1\).
solution
- (i) To find the critical points we set \(\partial f/\partial x = \partial f/\partial y =0\). Thus, \(2x - 1 = 0\), \(2y-1=0\), and hence \((x,y)=(\frac12, \frac12)\) is the only critical point in the open disc \(U = \{(x,y)\mid x^2 + y^2 <1\}\).
(ii) The boundary \(\partial U\) can be parametrized by \({\bf c}(t) = (\sin t,\cos t)\), \(0 \le t \le 2\pi\). Thus, \[ f({\bf c}(t)) = \sin^2 t + \cos^2 t -\sin t - \cos t +1= 2 - \sin t - \cos t = g(t). \]
To find the maximum and minimum of \(f\) on \(\partial U\), it suffices to locate the maximum and minimum of \(g\). Now \(g'(t)=0\) only when \[ \sin t = \cos t ,\qquad \hbox{that is, when} \qquad t = \frac{\pi}{4},\frac{5\pi}{4}. \]
Thus, the candidates for the maximum and minimum for \(f\) on \(\partial U\) are the points \({\bf c}({\pi}/{4}), {\bf c}({5\pi}/{4})\), and the endpoints \({\bf c}(0) = {\bf c}(2\pi)\).
- (iii) The values of \(f\) at the critical points are: \(f(\frac12,\frac12) = \frac12\) from step (i) and, from step (ii), \begin{eqnarray*} f\bigg({\bf c}\bigg(\frac{\pi}{4}\bigg)\bigg) &=& f\bigg(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\bigg) = 2-\sqrt{2},\\[5pt] f\bigg({\bf c}\bigg(\frac{5\pi}{4}\bigg)\bigg) &=& f\bigg(\!{-}\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\bigg) = 2 + \sqrt{2}, \end{eqnarray*} and \[ f({\bf c}(0)) = f({\bf c}(2\pi)) = f(0,1) = 1. \]
- (iv) Comparing all the values \(\frac12,2-\sqrt{2}, 2+\sqrt{2},1\), it is clear that the absolute minimum is \(\frac{1}{2}\) and the absolute maximum is \(2+\sqrt{2}\).
In Section 3.5, we shall consider a generalization of the strategy for finding the absolute maximum and minimum to regions \(D\) in \({\mathbb R}^n\).