Review Exercises for Chapter 5
Evaluate the integrals in Exercises 1 to 4.
Question 5.105
\(\displaystyle\int^3_0\!\int^{x^2 +1}_{-x^2 +1} {\it xy}\, {\it dy}\, {\it dx} \)
Question 5.106
\(\displaystyle\int^1_0\!\int^{1}_{\sqrt{x}}\, (x + y)^2 {\it dy}\, {\it dx} \)
Question 5.107
\(\displaystyle\int^1_0\!\int^{e^{2x}}_{e^x} x \ln y\, {\it dy}\, {\it dx} \)
Question 5.108
\(\displaystyle\int^1_0\!\int^2_1\!\int^3_2\cos\, [\pi(x+y+z)]\,{\it dx}\,{\it dy}\,{\it dz}.\)
Reverse the order of integration of the integrals in Exercises 5 to 8 and evaluate.
Question 5.109
The integral in Exercise 1
Question 5.110
The integral in Exercise 2
Question 5.111
The integral in Exercise 3
Question 5.112
The integral in Exercise 4
Question 5.113
Evaluate the integral \(\int^1_0\int^x_0\int^y_0(y+xz)\,dz\,{\it dy}\,{\it dx}.\)
Question 5.114
Evaluate \(\int^1_0\int^{y^2}_ye^{x/y}\,{\it dx}\,{\it dy}.\)
Question 5.115
Evaluate \(\int^1_0\int^{\rm (arcsin\, {\it y})/{\it y}}_0 y\cos xy\,{\it dx}\,{\it dy}.\)
Question 5.116
Change the order of integration and evaluate \[ \int^2_0 \int^1_{y/2} (x + y)^2 {\it dx}\, {\it dy} . \]
Question 5.117
Show that evaluating \({\intop\!\!\!\intop}_D {\it dx}\, {\it dy} \), where \(D\) is a \(y\)-simple region, reproduces the formula from one-variable calculus for the area between two curves.
Question 5.118
Change the order of integration and evaluate \[ \int^1_0 \int^1_{y^{1/2}} (x^2 + y^3 x)\, {\it dx}\, {\it dy} . \]
Question 5.119
Let \(D\) be the region in the \(xy\) plane inside the unit circle \(x^2 + y^2 = 1\). Evaluate \({\intop\!\!\!\intop}_D f(x,y)\, {\it dx}\, {\it dy}\) in each of the following cases:
- (a) \(f(x,y) = xy\)
- (b) \(f(x,y) = x^2 y^2\)
- (c) \(f(x,y) = x^3 y^3\)
Question 5.120
Find \({\intop\!\!\!\intop}_D y[1-\cos\, (\pi x/4)] {\it dx}\, {\it dy} \), where \(D\) is the region in Figure 5.38.
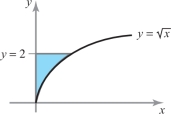
305
Evaluate the integrals in Exercises 17 to 24. Sketch and identify the type of the region (corresponding to the way the integral is written).
Question 5.121
\(\displaystyle\int^{\pi}_0 \int^{3 \sin x}_{\sin x} x(1 + y)\, {\it dy}\, {\it dx} \)
Question 5.122
\(\displaystyle\int^{1}_0 \int^{x \cos\, (\pi x/2)}_{x-1} (x^2 +xy +1)\, {\it dy}\, {\it dx} \)
Question 5.123
\(\displaystyle\int^{1}_{-1} \int^{(2-y)^2}_{y^{2/3}} \left(\frac{3}{2}\sqrt{x} - 2y\right)\, {\it dx}\, {\it dy}\)
Question 5.124
\(\displaystyle\int^{2}_0 \int^{3 (\sqrt{4 - x^2})/2}_{-3 (\sqrt{4 - x^2})/2} \left({\displaystyle \frac{5}{\sqrt{2+x}}} + y^3\right) \! {\it dy}\, {\it dx} \)
Question 5.125
\(\displaystyle\int^{1}_{0} \int^{x^2}_0 (x^2 + xy -y^2)\, {\it dy}\, {\it dx} \)
Question 5.126
\(\displaystyle\int^{4}_{2} \int^{y^3}_{y^2-1} 3 {\it dx}\, {\it dy} \)
Question 5.127
\(\displaystyle\int^{1}_{0} \int^{x}_{x^2} (x + y)^2 {\it dy}\, {\it dx} \)
Question 5.128
\(\displaystyle\int^{1}_{0} \int^{3y}_{0} e^{x+y} {\it dx}\, {\it dy} \)
In Exercises 25 to 27, integrate the given function f over the given region D.
Question 5.129
\(f(x,y) = x-y\); \(D\) is the triangle with vertices (0, 0), (1, 0), and (2, 1).
Question 5.130
\(f(x,y) = x^3 y + \cos x\); \(D\) is the triangle defined by \(0 \leq x \leq \pi/2, 0 \leq y \leq x\).
Question 5.131
\(f(x,y) = x^2 + 2xy^2 +2\); \(D\) is the region bounded by the graph of \(y = -x^2 + x\), the \(x\) axis, and the lines \(x = 0\) and \(x = 2\).
In Exercises 28 and 29, sketch the region of integration, interchange the order, and evaluate.
Question 5.132
\(\displaystyle\int^{4}_{1} \int^{\sqrt{x}}_1 (x^2 + y^2)\, {\it dy}\, {\it dx} \)
Question 5.133
\(\displaystyle\int^{1}_{0} \int^{1}_{1-y} (x+ y^2)\, {\it dx}\, {\it dy} \)
Question 5.134
Show that \[ 4e^5 \leq \intop\!\!\!\intop\nolimits_{[1,3]\times [2,4]} e^{x^2 + y^2} {\it dA} \leq 4e^{25}. \]
Question 5.135
Show that \[ 4\pi \leq \intop\!\!\!\intop\nolimits_{D} ({x^2 + y^2 +1})\, {\it dx}\, {\it dy} \leq 20 \pi, \] where \(D\) is the disk of radius 2 centered at the origin.
Question 5.136
Suppose \(W\) is a path-connected region; that is, given any two points of \(W\) there is a continuous path joining them. If \(f\) is a continuous function on \(W\), use the intermediate-value theorem to show that there is at least one point in \(W\) at which the value of \(f\) is equal to the average of \(f\) over \(W\); that is, the integral of \(f\) over \(W\) divided by the volume of \(W\). (Compare this with the mean-value theorem for double integrals.) What happens if \(W\) is not connected?
Question 5.137
Prove: \(\int^x_0 [ \int^t_0 F(u)\, {\it {\,d} u}] {\it {\,d} t} = \int^x_0 (x-u) F(u) \,{\it du}\).
Evaluate the integrals in Exercises 34 to 36.
Question 5.138
\(\displaystyle\int^1_0\int^z_0\int^y_0 xy^2z^3 {\it dx}\,{\it dy}\,{\it dz}\)
Question 5.139
\(\displaystyle\int^1_0\int^y_0\int_0^{x/\sqrt{3}}\displaystyle \frac{x}{x^2+z^2}{\it dz}\,{\it dx}\,{\it dy}\)
Question 5.140
\(\displaystyle\int^2_1\int^z_1\int^2_{1/y}yz^2 {\it dx}\,{\it dy}\,{\it dz}\)
Question 5.141
Write the iterated integral \(\int^1_0\int^1_{1-x}\int^1_xf(x,y,z)\,{\it dz}\,{\it dy}\,{\it dx}\) as an integral over a region in \({\mathbb R}^3\) and then rewrite it in five other possible orders of integration.
306
1Readers not already familiar with this idea should review the appropriate sections of their introductory calculus text.
2Such \({\bf c}_{\it jk}\) exist by virtue of the continuity of \(f\) on \(R\); see Theorem 7 in Section 3.3.
3This states that if \(g(x)\) is continuous on \([a,b]\), then \(\int_a^b g (x)\, {\it dx} =g(c)(b-a)\) for some point \(c\in [a,b]\). The more general second mean-value theorem was proved in Section 3.2.