exercises
Question 7.30
Evaluate the line integral \[ \int_{C} \textbf{F} \cdot \,{\it ds}, \] where \(\textbf{F}(x,y)= y^2 \textbf{i} - {\it xy} \textbf{j}\) and \(C\) is the part of the circle \(x^2 + y^2 = 1\) that starts at \((1,0)\) and ends at \((0,1)\), oriented counterclockwise.
Question 7.31
Repeat Problem 1 for \(\textbf{F}= y^2 \textbf{i} + 2{\it xy} \textbf{j}\), where \(C\) is the entire unit circle \(x^2 + y^2 = 1\).
Question 7.32
Let \({\bf F}(x,y,z)=x{\bf i}+y{\bf j}+z{\bf k}\). Evaluate the integral of \({\bf F}\) along each of the following paths:
- (a) \({\bf c}(t)=(t,t,t),\qquad 0\leq t\leq 1\)
- (b) \({\bf c}(t)=(\cos t,\sin t, 0),\qquad 0\leq t\leq 2 \pi\)
- (c) \({\bf c}(t)=(\sin t,0,\cos t),\qquad 0\leq t\leq 2 \pi\)
- (d) \({\bf c}(t)=(t^2,3t,2t^3),\qquad {-}1 \leq t\leq 2\)
Question 7.33
Evaluate each of the following line integrals:
- (a) \(\int_{\bf c} x \,{\it dy} -y \,{\it dx} ,\qquad {\bf c}(t)=(\cos t,\sin t), 0\leq t\leq 2\pi\)
- (b) \(\int_{\bf c} x \,{\it dx} + y \,{\it dy} ,\qquad {\bf c}(t)=(\cos \pi t,\sin \pi t), 0\leq t\leq 2\)
- (c) \(\int_{\bf c} yz \,{\it dx} +xz \,{\it dy} + {\it xy} \,{\it dz}\), where \({\bf c} \) consists of straight-line segments joining \((1, 0, 0)\) to \((0, 1, 0)\) to \((0, 0, 1)\)
- (d) \(\int_{\bf c} x^2 \,{\it dx} -{\it xy} \,{\it dy} + \,{\it dz}\), where \({\bf c}\) is the parabola \(z = x^2, y = 0\) from \((-1, 0, 1)\) to \((1, 0, 1)\).
Question 7.34
Consider the force field \({\bf F}(x,y,z)=x{\bf i}+y{\bf j}+z{\bf k}\). Compute the work done in moving a particle along the parabola \(y=x^2,z=0\), from \(x=-1\) to \(x=2\).
Question 7.35
Let \({\bf c}\) be a smooth path.
- (a) Suppose \({\bf F}\) is perpendicular to \({\bf c}'(t)\) at the point \({\bf c}(t)\). Show that \[ \int_{\bf c}{\bf F}\, {\cdot}\, \,d{\bf s} =0. \]
- (b) If \({\bf F}\) is parallel to \({\bf c}'(t)\) at \({\bf c}(t)\), show that \[ \int_{\bf c}{\bf F}\, {\cdot}\, \,d{\bf s} =\int_{\bf c}\|{\bf F}\| \,{\it ds} . \] [By parallel to \({\bf c}'(t)\) we mean that \({\bf F}({\bf c}(t))=\lambda (t){\bf c}'(t)\), where \(\lambda (t) > 0\).]
Question 7.36
Suppose the path \({\bf c}\) has length \(l\), and \(\|{\bf F}\|\leq M\). Prove that \[ \Big| \int_{\bf c}{\bf F}\, {\cdot}\, \,d{\bf s} \Big| \leq Ml. \]
Question 7.37
Evaluate \(\int_{\bf c}{\bf F}\, {\cdot}\, \,d{\bf s}\), where \({\bf F}(x,y,z)=y{\bf i}+2x{\bf j}+y{\bf k}\) and the path \({\bf c}\) is defined by \({\bf c} (t)=t{\bf i}+t^2{\bf j}+t^3{\bf k}\), \(0 \leq t\leq 1\).
Question 7.38
Evaluate \[ \int_{\bf c}y \,{\it dx} +(3y^3-x) \,{\it dy} +z \,{\it dz} \] for each of the paths \({\bf c}(t)=(t,t^n,0),0\leq t\leq 1\), where \(n=1,2,3, \ldots\).
Question 7.39
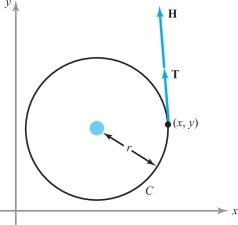
This exercise refers to Example 12. Let \(L\) be a very long wire, a planar section of which (with the plane perpendicular to the wire) is shown in Figure 7.19.
374
Suppose this plane is the \({\it xy}\) plane. Experiments show that \({\bf H}\) is tangent to every circle in the \({\it xy}\) plane whose center is the axis of \(L\), and that the magnitude of \({\bf H}\) is constant on every such circle \(C\). Thus, \({\bf H} = H{\bf T}\), where \({\bf T}\) is a unit tangent vector to \(C\) and \(H\) is some scalar. Using this information, show that \(H=I/2\pi r\), where \(r\) is the radius of circle \(C\) and \(I\) is the current flowing in the wire.
Question 7.40
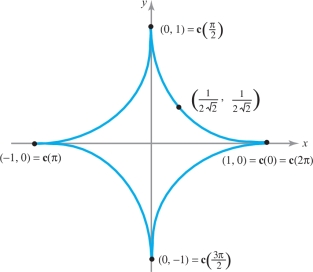
The image of the path \(t\mapsto (\cos^3t,\sin^3 t),0\leq t\leq 2\pi\) in the plane is shown in Figure 7.20. Evaluate the integral of the vector field \({\bf F}(x,y)=x{\bf i}+y{\bf j}\) around this curve.
Question 7.41
Suppose \({\bf c}_1\) and \({\bf c}_2\) are two paths with the same endpoints and \({\bf F}\) is a vector field. Show that \(\int_{{\bf c}_1}{\bf F}\, {\cdot}\, \,d{\bf s} = \int_{{\bf c}_2} {\bf F} \, {\cdot}\, \,d{\bf s}\) is equivalent to \(\int_c {\bf F}\, {\cdot}\, \,d{\bf s} =0\), where \(C\) is the closed curve obtained by first moving along \({\bf c}_1\) and then moving along \({\bf c}_2\) in the opposite direction.
Question 7.42
Let \({\bf c}(t)\) be a path and \({\bf T}\) the unit tangent vector. What is \(\int_{\bf c} {\bf T}\, {\cdot}\, \,d{\bf s}\)?
Question 7.43
Let \({\bf F}=(z^3+2{\it xy}){\bf i}+x^2{\bf j}+3xz^2{\bf k}\). Show that the integral of \({\bf F}\) around the circumference of the unit square with vertices \((\pm 1,\pm 1)\) is zero.
Question 7.44
Using the path in Exercise 11, observe that a \(C^1\) map \({\bf c}\colon\, [a,b]\to {\mathbb R}^3\) can have an image that does not “look smooth.” Do you think this could happen if \({\bf c}' (t)\) were always nonzero?
Question 7.45
What is the value of the integral of a gradient field around a closed curve \(C\)?
Question 7.46
Evaluate the line integral \[ \int_C 2{\it xyz} \,{\it dx} +x^2z \,{\it dy}+x^2 y\,{\it dz} , \] where \(C\) is an oriented simple curve connecting \((1, 1, 1)\) to \((1, 2, 4)\).
Question 7.47
Suppose \(\nabla\! f(x,y,z)=2{\it xyz}e^{x^2}{\bf i}+ze^{x^2}{\bf j}+ye^{x^2}{\bf k}\). If \(f(0,0,0) =5\), find \(f (1, 1, 2)\).
Question 7.48
Consider the gravitational force field (with \(G = m = M = 1\)) defined [for \((x, y, z)\neq (0, 0, 0)]\) by \[ {\bf F}(x,y,z)=-\frac{1}{(x^2+y^2+z^2)^{3/2}}\,(x{\bf i}+y{\bf j}+z{\bf k}) . \]
Show that the work done by the gravitational force as a particle moves from \((x_1,y_1,z_1)\) to \((x_2,y_2,z_2)\) along any path depends only on the radii \(R_1={\textstyle\sqrt{x_1^2 + y_1^2 + z_1^2}}\) and \(R_2={\textstyle\sqrt{x_2^2 + y_2^2 + z_2^2}}\).
Question 7.49
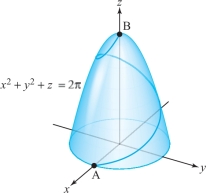
A cyclist rides up a mountain along the path shown in Figure 7.21. She makes one complete revolution around the mountain in reaching the top, while her vertical rate of climb is constant. Throughout the trip she exerts a force described by the vector field \[ {\bf F}(x,y,z)= y{\bf i} + x{\bf j} + {\bf k}. \]
What is the work done by the cyclist in traveling from A to B? What is unrealistic about this model of a cyclist?
Question 7.50
Let \({\bf c}\colon\, [a,b]\to {\mathbb R}^3\) be a path such that \({\bf c}'(t)\neq {\bf 0}\). Recall from Section 4.1 that when this condition holds, \({\bf c}\) is said to be regular. Let the function \(f\) be defined by the formula \(f(x) = \int^x_a\|{\bf c}'(t)\|\,{\it dt}\).
- (a) What is \(df/{\it dx}\)?
- (b) Using the answer to part (a), prove that \(f\colon\, [a,b]\to [0,L]\), where \(L\) is the length of \({\bf c}\), has a differentiable inverse \(g\colon\, [0,L]\to [a,b]\) satisfying \(f\circ g(s)=s,g\circ f(x)=x\). (You may use the one-variable inverse function theorem stated at the beginning of Section 3.5.)
- (c) Compute \(dg/{\it ds}\).
- (d) Recall that a path \(s\mapsto {\bf b}(s)\) is said to be of unit speed, or parametrized by arc length, if \(\|{\bf b}' (s)\|=1\). Show that the reparametrization of \({\bf c}\) given by \({\bf b}(s)={\bf c}\circ g(s)\) is of unit speed. Conclude that any regular path can be reparametrized by arc length. (Thus, for example, the Frenet formulas in Exercise 23 of Section 4.2 can be applied to the reparametrization \({\bf b}\).)
375
Question 7.51
Along a “thermodynamic path” \(C\) in \((V, T, P)\) space,
- (i) The heat gained is \(\int_C \Lambda_V \,dV+K_V\,dT\), where \(\Lambda_V,K_V\) are functions of \((V, T, P)\), depending on the particular physical system.
- (ii) The work done is \(\int_C P \,dV\).
For a van der Waals gas, we have \begin{eqnarray*} &&P(V,T) = \frac{RT}{V-b}-\frac{a}{V^2}, \qquad J\Lambda_V = \frac{RT}{V-b},\\[5pt] && \hbox{and }\qquad K_V = \hbox{constant,} \end{eqnarray*} where \(R, b, a\), and \(J\) are known constants. Initially, the gas is at a temperature \(T_0\) and volume \(V_0\).
- (a) An adiabatic process is a thermodynamic motion \((V(t), T(t), P(t))\) for which \[ \frac{dT}{dV}=\frac{dT/{\it dt}}{dV/{\it dt}}=-\frac{\Lambda_V}{K_V}. \] If the van der Waals gas undergoes an adiabatic process in which the volume doubles to \(2V_0\), compute
- (1) the heat gained;
- (2) the work done; and
- (3) the final volume, temperature, and pressure.
- (b) After the process indicated in part (a), the gas is cooled (or heated) at constant volume until the original temperature \(T_0\) is achieved. Compute
- (1) the heat gained;
- (2) the work done; and
- (3) the final volume, temperature, and pressure.
- (c) After the process indicated in part (b), the gas is compressed until the gas returns to its original volume \(V_0\). The temperature is held constant throughout the process. Compute
- (1) the heat gained;
- (2) the work done; and
- (3) the final volume, temperature, and pressure.
- (d) For the cyclic process described in parts (a), (b), (c), compute
- (1) the total heat gained; and
- (2) the total work done.