8.3 Stokes’ Theorem

Stokes’ theorem relates the line integral of a vector field around a simple closed curve \(C\) in \({\mathbb R}^3\) to an integral over a surface \(S\) for which \(C\) is the boundary. In this regard it is very much like Green’s theorem.

Stokes’ Theorem for Graphs

Let us begin by recalling a few facts from Chapter 7. Consider a surface \(S\) that is the graph of a function \(f (x,y)\), so that \(S\) is parametrized by \[ \left\{ \begin{array}{l} x=u \\ y=v \\ z = f (u,v) = f (x,y) \end{array}\right. \] for \((u,v)\) in some domain \(D\) in the plane. The integral of a vector function \({\bf F}\) over \(S\) was developed in Section 7.6 as \begin{equation} \intop\!\!\!\intop\nolimits_{S} {\bf F} \,{\cdot}\, d {\bf S} = \intop\!\!\!\intop\nolimits_{D} \left[ F_1 \left( - \frac{\partial z}{\partial x} \right)+ F_2 \left( - \frac{\partial z}{\partial y} \right)+ F_3 \right] {\it dx}\, {\it dy}, \end{equation} where \({\bf F} = F_1 {\bf i}+ F_2 {\bf j}+ F_3 {\bf k}\).

In Section 8.2, we first assumed that the regions \(D\) under consideration were simple; while this was used in our proof of Green’s theorem, we noted there that the theorem is valid for a wider class of regions. In this section we assume that \(D\) is a region whose boundary is a simple closed curve and to which Green’s theorem applies. Green’s theorem involves choosing an orientation on the boundary of \(D\), as was explained in Section 8.2. The choice of orientation that validates Green’s theorem will be called positive. Recall that if \(D\) is simple, then the positive orientation is the counterclockwise one.

Suppose that \({\bf c} \colon\, [a,b] \to {\mathbb R}^2, {\bf c} (t) = (x (t), y(t))\) is a parametrization of \(\partial\! D\) in the positive direction. Then we define the boundary curve \(\partial\! S\) to be the oriented simple closed curve that is the image of the mapping \({\bf p} \colon\, t \mapsto (x(t), y(t), f (x(t), y(t)))\) with the orientation induced by \({\bf p}\) (Figure 8.11).

Figure 8.11: The induced orientation on \(\partial\! S\): As you walk around the boundary, the surface should be on your left.

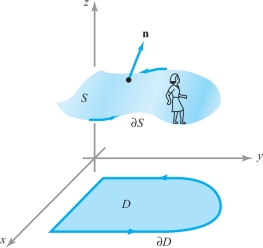
To remember this orientation (i.e., the positive direction) on \(\partial\! S\), imagine that you are an “observer” walking along the boundary of the surface with the normal as your upright direction; you are moving in the positive direction if the surface is on your left. This orientation on \(\partial\! S\) is often called the orientation induced by an upward normal \({\bf n}\).

Remember that \(\int_{\partial S} {\bf F} \,{\cdot}\,d {\bf s}\) is the integral around \(\partial\! S\) of the tangential component of \({\bf F}\), while \({\intop\!\!\!\intop}_S {\bf G} \,{\cdot}\, d {\bf S}\) is the integral over \(S\) of \({\bf G} \,{\cdot}\, {\bf n}\), the normal component of \({\bf G}\) (see Sections 7.2 and 7.6). Thus, Stokes’ theorem says that the integral of the normal component of the curl of a vector field \({\bf F}\) over a surface \(S\) is equal to the integral of the tangential component of \({\bf F}\) around the boundary \(\partial\! S\).

example 2

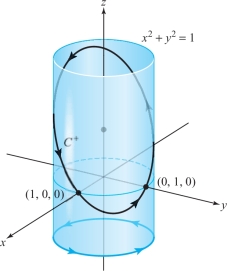
Use Stokes’ theorem to evaluate the line integral \[ \int_C - y^3 {\it {\,d} x}+x^3 {\it dy} - z^3 {\,d} z, \] where \(C\) is the intersection of the cylinder \(x^2 + y^2=1\) and the plane \(x+ y + z=1\), and the orientation on \(C\) corresponds to counterclockwise motion in the \(xy\) plane.

solution The curve \(C\) bounds the surface \(S\) defined by the equation \(z= 1-x-y=f(x,y)\) for \((x, y)\) in the set \(D = \{(x,y) \mid x^2 + y^2 \le 1\}\) (Figure 8.12). We set \({\bf F} = - y^3 {\bf i} + x^3 {\bf j} - z^3 {\bf k}\), which has curl \({ \nabla} \times {\bf F} = ( 3x^2 + 3 y^2) {\bf k}\). Then, by Stokes’ theorem, the line integral is equal to the surface integral \[ \intop\!\!\!\intop\nolimits_{S} ( {\nabla} \times {\bf F}) \,{\cdot}\, d {\bf S}. \]

But \({ \nabla} \times {\bf F}\) has only a \({\bf k}\) component. Thus, by formula (1) we have \[ \intop\!\!\!\intop\nolimits_{S}( {\nabla} \times {\bf F}) \,{\cdot}\,d {\bf S}=\intop\!\!\!\intop\nolimits_{D}(3x^2+3y^2)\,{\it {\,d} x}\,{\it dy}. \]

Figure 8.12: The curve \(C\) is the intersection of the cylinder \(x^{2} + y^{\,2} = 1\) and the plane \(x+y+z = 1\).

443

This integral can be evaluated by changing to polar coordinates. Doing this, we get \[ 3 \intop\!\!\!\intop\nolimits_{D} (x^2 + y^2)\, {\it {\,d} x}\,{\it dy} =3 \int_0^1 \int_0^{2 \pi} r^2 \,{\cdot}\, r {\,d} \theta {\,d} r = 6 \pi \int_0^1 r^3 {\,d} r = \frac{6 \pi}{4} = \frac{3 \pi}{2}. \]

Let us verify this result by directly evaluating the line integral \[ \int_C - y^3 {\it {\,d} x}+ x^3 \,{\it dy}- z^3 {\,d} z. \]

We can parametrize the curve \(\partial\! D\) by the equations \[ x = \cos t , \qquad y = \sin t,\qquad z=0, \qquad 0 \le t \le 2 \pi. \]

The curve \(C\) is therefore parametrized by the equations \[ x = \cos t, \qquad y = \sin t, \qquad z =1-\sin t - \cos t, \qquad 0 \le t \le 2 \pi. \]

Thus, \begin{eqnarray*} && \int_C \,-\, y^3 {\it {\,d} x} + x^3 {\it dy} - z^3 {\,d} z \\[2pt] &&\quad = \int_0^{2 \pi}[(-\sin^3 t) ( -\sin t) + ( \cos^3 t) ( \cos t) \\[5pt] &&\qquad{-}\,( 1-\sin t -\cos t)^3 (-\cos t + \sin t)]\, {\it {\,d} t} \\[5pt] &&\quad = \int_0^{2 \pi} ( \cos^4 t + \sin^4 t) \,{\it {\,d} t} - \int_0^{2 \pi} ( 1-\sin t -\cos t)^3 ( -\cos t + \sin t) \,{\it {\,d} t}.\\[-12pt] \end{eqnarray*}

The second integrand is of the form \(u^3 {\,d} u\), where \(u=1 -\sin t - \cos t\), and thus the integral is equal to \[ {\displaystyle \frac{1}{4}} [(1 - \sin t - \cos t)^4 ]^{2 \pi}_0=0. \]

Hence, we are left with \[ \int_0^{2 \pi} ( \cos^4 t+ \sin^4 t ) \,{\it {\,d} t}. \]

This integral can be evaluated using formulas (18) and (19) of the table of integrals. We can also proceed as follows. Using the trigonometric identities \[ \sin^2 t= \frac{1- \cos 2t}{2}, \cos^2 t = \frac{1 + \cos 2 t}{2}, \] substituting and squaring these expressions, we reduce the preceding integral to \[ \frac{1}{2} \int_0^{2 \pi}( 1+ \cos^2 2t)\,{\it {\,d} t} = \pi + \frac{1}{2} \int_0^{2 \pi}\cos^2 2 t \,{\it {\,d} t}. \]

Again using the identity \(\cos^2 2 t = (1+ \cos 4t)/2\), we find \begin{eqnarray*} \pi + \frac{1}{4}\int_0^{2 \pi}( 1+ \cos 4t) \,{\it {\,d} t} &= & \pi + \frac{1}{4} \int_0^{2 \pi}\,{\it {\,d} t} + \frac{1}{4}\int_0^{2 \pi}\cos\, 4t \,{\it {\,d} t} \\[6pt] & = & \pi + \frac{\pi}{2}+ 0 = \frac{3 \pi}{2}. \\[-32pt] \end{eqnarray*}

Stokes’ Theorem for Parametrized Surfaces

To simplify the proof of Stokes’ theorem given earlier, we assumed that the surface \(S\) could be described as the graph of a function \(z = f (x,y), (x,y) \in D\), where \(D\) is some region to which Green’s theorem applies. However, without too much more effort we can obtain a more general theorem for oriented parametrized surfaces \(S\). The main complication is in the definition of \(\partial\! S\).

Suppose \({\Phi} \colon\, D \to {\mathbb R}^3\) is a parametrization of a surface \(S\) and \({\bf c} (t) = ( u (t) , v (t))\) is a parametrization of \(\partial\! D\). We might be tempted to define \(\partial\! S\) as the curve parametrized by \(t \mapsto {\bf p} (t) = {\Phi} ( u (t), v (t))\). However, with this definition, \(\partial\! S\) might not be the boundary of \(S\) in any reasonable geometric sense.

For example, we would conclude that the boundary of the unit sphere \(S\) parametrized by spherical coordinates in \({\mathbb R}^3\) is half of the great circle on \(S\) lying in the \(xz\) plane, but clearly in a geometric sense \(S\) is a smooth surface (no points or cusps) with no boundary or edge at all (see Figure 8.13 and Exercise 20). Thus, this great circle is in some sense the “mistaken” boundary of \(S\).

Figure 8.13: The surface \(S\) is a portion of a sphere.

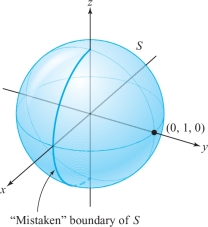
We can get around this difficulty by assuming that \({\Phi}\) is one-to-one on all of \(D\). Then the image of \(\partial\! D\) under \({\Phi}\), namely, \({\Phi} ( \partial\! D)\), will be the geometric boundary of \(S = {\Phi} (D)\). If \({\bf c} (t) = (u (t), v (t))\) is a parametrization of \(\partial\! D\) in the positive direction, we define \(\partial\! S\) to be the oriented simple closed curve that is the image of the mapping \({\bf p}\colon\, t \mapsto {\Phi} ( u (t), v (t))\), with the orientation of \(\partial\! S\) induced by \({\bf p}\) (see Figure 8.11).

This is proved in the same way as Theorem 5.

example 3

Let \(S\) be the surface shown in Figure 8.14, with the indicated orientation. Let \({\bf F} = y {\bf i} - x {\bf j} + e^{xz} {\bf k}\). Evaluate \({\intop\!\!\!\intop}_S\ ( { \nabla} \times {\bf F}) \,{\cdot}\, d {\bf S}\).

445

Figure 8.14: This surface \(S\) is a portion of a sphere sitting on top of the circle \(x^2+y^{\,2}=1\). It does not include the disc \(x^2+y^{\,2}<1\) in the \(xy\) plane.

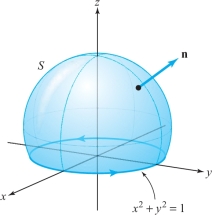
solution This surface could be parametrized using spherical coordinates based at the center of the sphere. However, we need not explicitly find \({\Phi}\) in order to solve this problem. By Theorem 6, \({\intop\!\!\!\intop}_S\ ( {\nabla} \times {\bf F}) \,{\cdot}\, d {\bf S}= \int_{\partial\! S}{\bf F}{\cdot} {\,d} {\bf s}\), and so if we parametrize \(\partial\! S\) by \(x (t) = \cos t, y (t) = \sin t , 0 \le t \le 2 \pi\), we determine \[ \int_{\partial\! S}{\bf F} \,{\cdot}\,d {\bf s} = \int_0^{2 \pi} \Big( y \frac{{\it dx}}{{\it dt}}- x \frac{{\it dy}}{{\it dt}} \Big)\, {\it dt} = \int_0^{2 \pi} ( - \sin^2 t- \cos^2 t) \,{\it {\,d} t} = - \int_0^{2 \pi}\,{\it {\,d} t} =- 2 \pi \] and therefore \({\intop\!\!\!\intop}_S\ ({\nabla} \times {\bf F}) \,{\cdot}\, d {\bf S} = - 2 \pi\).

The Curl as Circulation per Unit Area

Let us now use Stokes’ theorem to justify the physical interpretation of \({\nabla} \times {\bf F}\) in terms of paddle wheels that was proposed in Chapter 4. Paraphrasing Theorem 6, we have \[ \intop\!\!\!\intop\nolimits_{S} (\hbox{curl } {\bf F}) \,{\cdot}\, {\bf n}\, {\it {\,d} S} = \intop\!\!\!\intop\nolimits_{S} (\hbox{curl } {\bf F}) \,{\cdot}\, {\,d} {\bf S} = \int_{\partial\! S} {\bf F} \,{\cdot}\, {\,d} {\bf s} = \int_{\partial\! S} F_T {\,d} s, \] where \(F_T\) is the tangential component of \({\bf F}\). This says that the integral of the normal component of the curl of a vector field over an oriented surface \(S\) is equal to the line integral of \({\bf F}\) along \(\partial\! S\), which in turn is equal to the path integral of the tangential component of \({\bf F}\) over \(\partial\! S\).

Suppose \({\bf V}\) represents the velocity vector field of a fluid. Consider a point P and a unit vector \({\bf n}\). Let \(S_\rho\) denote the disc of radius \(\rho\) and center P, which is perpendicular to \({\bf n}\). By Stokes’ theorem, \[ \intop\!\!\!\intop\nolimits_{{S_\rho}} \hbox{curl } {\bf V} \,{\cdot}\, d {\bf S} = \intop\!\!\!\intop\nolimits_{S_\rho} \hbox{curl } {\bf V} \,{\cdot}\, {\bf n}\,{\it {\,d} S} = \int_{\partial\! S_\rho} {\bf V} \,{\cdot}\, d {\bf s}, \] where \(\partial\! S_\rho\) has the orientation induced by \({\bf n}\) (see Figure 8.15).

Figure 8.15: A normal \({\bf n}\) induces an orientation on the boundary \(\partial\! S_{\rho}\) of the disc \(S_{\rho }\).

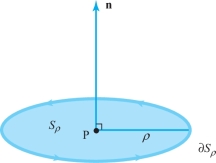
By the mean-value theorem for integrals (Exercise 16, Section 7.6), there is a point Q in \(S_\rho\) such that \[ \intop\!\!\!\intop\nolimits_{{S_\rho}} \hbox{curl } {\bf V} \,{\cdot}\, {\bf n} {\,d} S = [ \hbox{curl }{\bf V} ({\rm Q}) \,{\cdot}\, {\bf n} ] A ( S_\rho), \] where \(A(S_\rho)=\pi \rho^2\) is the area of \(S_\rho\) and curl \({\bf V} ({\rm Q})\) is the value of curl \({\bf V}\) at Q. Thus, \begin{eqnarray*} {\mathop{\rm limit}_{\rho \to 0}}\ \frac{1}{A(S_\rho)} \int_{\partial\! S_\rho} {\bf V} \,{\cdot}\, d {\bf s} & = & {\mathop{\rm limit}_{\rho \to 0}}\ \frac{1}{A(S_\rho)} \intop\!\!\!\intop\nolimits_{{S_\rho}} (\hbox{curl } {\bf V}) \,{\cdot}\, d {\bf S} \\[6pt] & = &{\mathop {\rm limit}_{\rho \to 0}} \hbox{ curl } {\bf V} ({\rm Q}) \,{\cdot}\, {\bf n} = \hbox{curl } {\bf V} ({\rm P}) \,{\cdot}\, {\bf n}.\\[-10pt] \end{eqnarray*}

Thus,footnote # \begin{equation} \hbox{curl } {\bf V} ( {\rm P}) \,{\cdot}\, {\bf n}={\mathop {\rm limit}_{\rho \to 0}}\ \frac{1}{A(S_\rho)} \int_{\partial\! S_\rho} {\bf V} \,{\cdot}\, d {\bf s}.\\[-4pt] \end{equation}

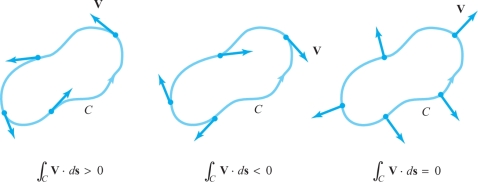
Let us pause to consider the physical meaning of \(\int_C {\bf V} \,{\cdot}\, d {\bf s}\) when \({\bf V}\) is the velocity field of a fluid. Suppose, for example, that \({\bf V}\) points in the direction tangent to the oriented curve \(C\) (Figure 8.16). Then clearly \(\int_C {\bf V} \,{\cdot}\, d {\bf s} > 0\), and particles on \(C\) tend to rotate counterclockwise. If \({\bf V}\) is pointing in the opposite direction, then \(\int_C {\bf V} \,{\cdot}\, d {\bf s} < 0\) and particles tend to rotate clockwise. If \({\bf V}\) is perpendicular to \(C\), then particles don't rotate on \(C\) at all and \(\int_C {\bf V} \,{\cdot}\, d {\bf s}=0\). In general, \(\int_C {\bf V} \,{\cdot}\, d {\bf s}\), being the integral of the tangential component of \({\bf V}\), represents the net amount of turning of the fluid in a counterclockwise direction around \(C\). We therefore refer to \(\int_C {\bf V} \,{\cdot}\, d {\bf s}\) as the circulation of \({\bf V}\) around \(C\) (see Figure 8.17).

Figure 8.16: The intuitive meaning of the possible signs of \(\int_{C} {\bf V }\,{\cdot} \,d\,{\bf s}\).

Figure 8.17: Circulation of a vector field (velocity field of a fluid): (a) Circulation about \(C\) is zero; (b) nonzero circulation about \(C\) (“whirlpool”).

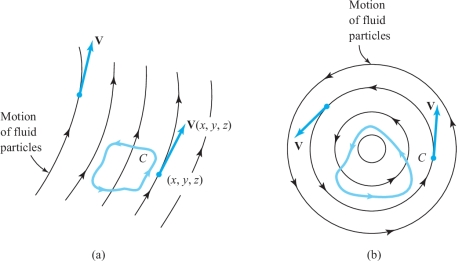
These results allow us to see just what curl \({\bf V}\) means for the motion of a fluid. The circulation \(\int_{\partial\! S_\rho} {\bf V} \,{\cdot}\, d {\bf s}\) is the net velocity of the fluid around \(\partial\! S_\rho\), so that (curl \({\bf V}) \,{\cdot}\, {\bf n}\) represents the turning or rotating effect of the fluid around the axis \({\bf n}\).

Observe that the magnitude of curl \({\bf V}{\rm (P)} \,{\cdot}\, {\bf n}\) is maximized when \({\bf n} = \hbox{curl } {\bf V} / \| \hbox{curl } {\bf V} \|\) (evaluated at P). Therefore, the rotating effect at P is greatest about the axis that is parallel to curl \({\bf V}/ \|\hbox{curl } {\bf V} \|\). Thus, curl \({\bf V}\) is aptly called the vorticity vector.

We can use these ideas to compute the curl in cylindrical coordinates.

example 4

Let the unit vectors \({\bf e}_r,{\bf e}_\theta, {\bf e}_z\) associated with cylindrical coordinates be as shown in Figure 8.18. Let \({\bf F}=F_r {\bf e}_r+F_\theta{\bf e}_\theta +F_z{\bf e}_z\). (The subscripts here denote components of \({\bf F}\), not partial derivatives.) Find a formula for the \({\bf e}_r\) component of \({\nabla} \times {\bf F}\) in cylindrical coordinates.

Figure 8.18: Orthonormal vectors \({\bf e}_{r}\), \({\bf e}_{\theta }\), and \({\bf e}_{z}\) associated with cylindrical coordinates. The vector \({\bf e}_{r}\) is parallel to the line labeled \(r\).

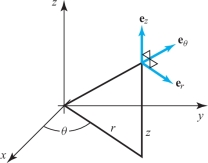
solution Let \(S\) be the surface shown in Figure 8.19.

Figure 8.19: A surface element in cylindrical coordinates.

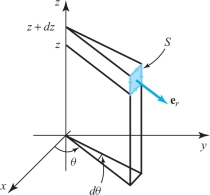
448

The area of \(S\) is \(r{\,d} \theta {\,d} z\) and the unit normal is \({\bf e}_r\). The integral of \(\bf F\) around the edges of \(S\) is approximately \begin{eqnarray*} && [F_\theta (r,\theta,z)-F_\theta (r,\theta,z+dz)]r{\,d} \theta+ [F_z(r,\theta+d \theta,z)-F_z(r,\theta,z)]{\,d} z\\[6pt] && \qquad\approx -\frac{\partial\! F_\theta}{\partial z}{\,d} z\, r{\,d} \theta + \frac{\partial\! F_z}{\partial \theta}\,d\theta\, d z. \end{eqnarray*}

Thus, the circulation per unit area is this expression divided by \(r {\,d} \theta\, d z\), namely, \[ \frac{1}{r}\frac{\partial\! F_z}{\partial \theta}-\frac{\partial\! F_\theta} {\partial z}. \]

According to the previous box, this must be the \({\bf e}_r\) component of the curl.

Gradient, Divergence, and Curl in Cylindrical and Spherical Coordinates

By similar arguments to Example 4, we find that the curl in cylindrical coordinates is given by \[ {\nabla} \times {\bf F}=\frac{1}{r} \left| \begin{array}{c@{\quad}c@{\quad}c} {\bf e}_r & r{\bf e}_{\theta} & {\bf e}_z\\[4pt] \displaystyle\frac{\partial\!}{\partial r} &\displaystyle\frac{\partial\!}{\partial \theta}&\displaystyle\frac{\partial\!}{\partial z}\\[8pt] F_r & {\it rF}_\theta & F_z \end{array} \right|. \]

We can find other important vector quantities expressed in different coordinate systems. For example, the chain rule shows that the gradient in cylindrical coordinates is \[ {\nabla}\! f=\frac{\partial\! f}{\partial r}\,{\bf e}_r +\frac{1}{r} \frac{\partial\! f}{\partial \theta}\,{\bf e}_\theta +\frac{\partial\! f}{\partial z}\,{\bf e}_z, \] and in Section 8.5 we will establish related techniques that give the following formula for the divergence in cylindrical coordinates: \[ {\nabla} \,{\cdot}\, {\bf F} =\frac{1}{r}\left[\frac{\partial\!}{\partial r}(r F_r)+ \frac{\partial\! F_\theta}{\partial \theta}+\frac{\partial\!}{\partial z}(r F_z)\right]. \]

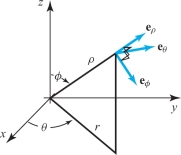
Corresponding formulas for gradient, divergence, and curl in spherical coordinates are \begin{eqnarray*} {\nabla}\! f &=& \frac{\partial\! f}{\partial\! \rho}\,{\bf e}_\rho+ \frac{1}{\rho} \frac{\partial\! f}{\partial \phi}\,{\bf e}_\phi +\frac{1}{\rho \sin \phi}\frac{\partial\! f}{\partial \theta}\,{\bf e}_\theta\\[6pt] {\nabla} \,{\cdot} \,{\bf F} &=& \frac{1}{\rho^2}\frac{\partial\!}{\partial\! \rho} (\rho^2 F_\rho)+\frac{1}{\rho \sin \phi}\frac{\partial\!}{\partial \phi}(\sin \phi F_\phi)+ \frac{1}{\rho \sin \phi}\frac{\partial\! F_\theta}{\partial \theta}\\[-15pt] \end{eqnarray*} and \begin{eqnarray*} {\nabla} \times {\bf F} &=&\left[ \frac{1}{\rho \sin \phi}\frac{\partial\!}{\partial \phi}(\sin \phi F_\theta)- \frac{1}{\rho \sin \phi}\frac{\partial\! F_\phi}{\partial \theta}\right]{\bf e}_\rho\\[6pt] && +\left[\frac{1}{\rho \sin \phi}\frac{\partial\! F_\rho}{\partial \theta}- \frac{1}{\rho}\frac{\partial\!}{\partial\! \rho}(\rho F_\theta)\right]{\bf e}_{\phi}+ \left[\frac{1}{\rho}\frac{\partial\!}{\partial\! \rho}(\rho F_\phi)-\frac{1}{\rho} \frac{\partial\! F_\rho}{\partial \phi}\right]{\bf e}_\theta, \end{eqnarray*} where \({\bf e}_\rho,{\bf e}_\phi,{\bf e}_\theta\) are as shown in Figure 8.20 and where \({\bf F}=F_\rho {\bf e}_\rho+F_\phi {\bf e}_\phi+F_\theta {\bf e}_\theta\).

Figure 8.20: Orthonormal vectors \({\bf e}_{\rho }\), \({\bf e}_{\phi }\), and \({\bf e}_{\theta }\) associated with spherical coordinates.

Faraday’s Law

Vector calculus plays an essential role in the theory of electromagnetism. The next example shows how Stokes’ theorem applies.

example 5

Let \({\bf E}\) and \({\bf H}\) be time-dependent electric and magnetic fields, respectively, in space. Let \(S\) be a surface with boundary \(C\). We define \begin{eqnarray*} \int_C {\bf E}\,{\cdot}\, d {\bf s} &=& \hbox{voltage around } C,\\[5pt] \intop\!\!\!\intop\nolimits_{S} {\bf H}\,{\cdot}\, d {\bf S} &=& \hbox{magnetic flux across } S.\\[-8pt] \end{eqnarray*}

Faraday’s law (see Figure 8.21) states that the voltage around C equals the negative rate of change of magnetic flux through S. Show that Faraday’s law follows from the following differential equation (one of the Maxwell equations): \[ {\nabla} \times {\bf E} =-\frac{\partial {\bf H}}{\partial t}. \]

Figure 8.21: Faraday’s law.

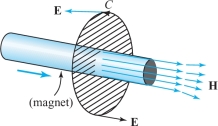
solution Assume that \(-\partial {\bf H}/\partial t={\nabla} \times {\bf E}\) holds. By Stokes’ theorem, \[ \int_C {\bf E}\,{\cdot}\, d {\bf s}=\intop\!\!\!\intop\nolimits_{S} ({\nabla} \times {\bf E})\,{\cdot}\, d {\bf S}. \]

Assuming that we can move \(\partial\!/\partial t\) under the integral sign, we get \[ -\frac{\partial\!}{\partial t}\intop\!\!\!\intop\nolimits_{S}{\bf H}\,{\cdot}\, d {\bf S}=\intop\!\!\!\intop\nolimits_{S} - \frac{\partial {\bf H}}{\partial t}\,{\cdot}\, d {\bf S}=\intop\!\!\!\intop\nolimits_{S} (\nabla \times {\bf E})\,{\cdot}\, d {\bf S}=\int_C {\bf E}\,{\cdot}\, d {\bf s} \] and so \[ \int_C {\bf E}\,{\cdot}\, d {\bf s} =-\frac{\partial\!}{\partial t}\intop\!\!\!\intop\nolimits_{S} {\bf H}\,{\cdot}\, d {\bf S}, \] which is Faraday’s law.

Falling Cats and Stokes’ Theorem

Have you ever wondered how a falling cat can right itself? Released from a resting position with its feet above its head, the cat is able to execute a 180\(^{\circ}\) reorientation and land safely on its feet. This well-known phenomenon has fascinated people for many years—especially in cities like New York, where cats have been known to survive falls of 8 to 30 stories!

There have been many incorrect explanations as to how cats are able to right themselves, including the idea that it has to do with how the cat twirls its tail. This cannot be right because Manx cats, which have no tails, can also perform this feat!

Figure 8.22: The falling cat rights itself by wriggling its body parts.

We observe, as in Figure 8.22, that the cat achieves this net change in orientation by wriggling, to create changes in its internal shape or configuration. On the surface, this provides a seeming contradiction; because the cat is dropped from a resting position, it has zero angular momentum at the beginning of the fall and hence, according to a basic law of physics called conservation of angular momentum, the cat has zero angular momentum throughout the duration of its fall.footnote # Amazingly, the cat has effectively changed its angular position while maintaining zero angular momentum!

The exact process by which this occurs is subtle; intuitive reasoning can lead one astray and, as we have indicated, many false explanations have been offered throughout the history of trying to solve this mystery.footnote # Recently, new and interesting insights have been discovered using geometric methods that, in fact, are related to curvature (see Section 7.7).footnote #

The way that curvature and geometry are related to the falling cat phenomenon is not easy to explain in full detail, but we can explain a similar phenomenon that is easy to understand. Interestingly, Stokes’ theorem is the key to understanding these types of phenomena.