10.2 Summing an Infinite Series
Many quantities that arise in applications cannot be computed exactly. We cannot write down an exact decimal expression for the number \(\pi\) or for values of the sine function such as \(\sin 1\). However, sometimes these quantities can be represented as infinite sums. For example, using Taylor series (Section 10.7), we can show that \[ \begin{equation*} \sin 1 = 1 - \frac1{3!}+\frac1{5!}-\frac1{7!} + \frac1{9!} -\frac1{11!} + \cdots \tag {1} \end{equation*} \] Infinite sums of this type are called infinite series.
What precisely does Eq.(1) mean? It is impossible to add up infinitely many numbers, but what we can do is compute the partial sums \(S_N\), defined as the finite sum of the terms up to and including \(N\) th term. Here are the first five partial sums of the infinite series for \(\sin 1\): \[ \begin{array}{rll} S_1 &{}= 1&\\ S_2 &{}= 1-\dfrac1{3!} = 1 - \dfrac1{6} &{}\approx 0.833\\ S_3 &{}= 1-\dfrac1{3!} + \dfrac1{5!} = 1 - \dfrac1{6}+\dfrac1{120} &{}\approx 0.841667\\ S_4 &{}= 1 - \dfrac1{6}+\dfrac1{120}-\dfrac1{5040} &{}\approx 0.841468 \\ S_5 &{}= 1 - \dfrac1{6}+\dfrac1{120}-\dfrac1{5040} +\dfrac1{362{,}880} &{}\approx \textbf{0.841470984}6 \end{array} \]
549
Compare these values with the value obtained from a calculator: \[ \sin 1 {}~\approx \mathbf{0.841470984}8079\qquad\textrm{(calculator value)} \]
We see that \(S_5\) differs from \(\sin 1\) by less than \(10^{-9}\). This suggests that the partial sums converge to \(\sin 1\), and in fact, we will prove that \[\sin 1 = \lim_{N\to\infty}S_N\]
(Example 2 in Section 10.7). So although we cannot add up infinitely many numbers, it makes sense to define the sum of an infinite series as a limit of partial sums.
- Infinite series may begin with any index. For example, \[ \sum_{n=3}^\infty \frac1n = \frac13+\frac14+\frac15+\cdots \] When it is not necessary to specify the starting point, we write simply \({\sum a_n}\).
- Any letter may be used for the index. Thus, we may write \(a_m\), \(a_k\), \(a_i\) etc.
In general, an infinite series is an expression of the form \[ \sum_{n = 1}^{\infty} a_n = a_1 + a_2 + a_3 + a_4 + \cdots \] where \(\{a_n\}\) is any sequence. For example,
| Sequence | General term | Infinite series |
| \(\frac13, \frac19, \frac1{27}, \ldots \) | \(a_n = \frac{1}{3^n}\) | \(\displaystyle\sum_{n = 1}^\infty \frac{1}{3^n} = \frac{1}{3} + \frac{1}{9} + \frac{1}{27} + \frac{1}{81} + \cdots\) |
| \(\frac{1}{1}, \frac14, \frac19, \frac1{16}, \ldots \) | \(a_n = \frac{1}{n^2}\) | \(\displaystyle\sum_{n = 1}^\infty \frac{1}{n^2} = \frac1{1}+\frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \cdots\) |
The \(N\) th partial sum \(S_N\) is the finite sum of the terms up to and including \(a_N\): \[ S_N = \sum_{n = 1}^{N} a_n = a_1 + a_2 + a_3 + \cdots + a_N \]
If the series begins at \(k\) then \(S_N = \sum_{n = k}^N a_n\).
DEFINITION Convergence of an Infinite Series
An infinite series \(\sum\limits_{n=k}^{\infty} a_n\) converges to the sum \(S\) if its partial sums converge to \(S\): \[\lim\limits_{N\to\infty}S_N =S\]
In this case, we write \(S = \sum\limits_{n=k}^\infty a_n\).
- If the limit does not exist, we say that the infinite series diverges.
- If the limit is infinite, we say that the infinite series diverges to infinity.
We can investigate series numerically by computing several partial sums \(S_N\). If the partial sums show a trend of convergence to some number \(S\), then we have evidence (but not proof) that the series converges to \(S\). The next example treats a telescoping series, where the partial sums are particularly easy to evaluate.
550
EXAMPLE 1 Telescoping Series
Investigate numerically: \[ S=\sum_{n=1}^{\infty} \frac{1}{n(n+1)} = \frac1{1(2)} + \frac1{2(3)} + \frac1{3(4)}+\frac1{4(5)} + \cdots \]
Then compute the sum \(S\) using the identity: \[ \frac1{n(n+1)} = \frac1n-\frac1{n+1} \]
| \(N\) | \(S_N\) |
| \(10\) | \(0.90909\) |
| \(50\) | \(0.98039\) |
| \(100\) | \(0.990099\) |
| \(200\) | \(0.995025\) |
| \(300\) | \(0.996678\) |
Solution The values of the partial sums listed in Table 10.2 suggest convergence to \(S = 1\) To prove this, we observe that because of the identity, each partial sum collapses down to just two terms: \[ \begin{eqnarray*} S_1 &=& \frac1{1(2)} = \frac11 - \frac12\\ S_2&=& \frac1{1(2)} + \frac1{2(3)} = \left(\frac11 - \cancel{\frac12}\right) +\left( \cancel{\frac12} - \frac13\right) = 1-\frac13\\ S_3 &=& \frac1{1(2)} + \frac1{2(3)} + \frac1{3(4)} = \left( \frac11 - \cancel{\frac12}\right) +\left( \cancel{\frac12} - \cancel{\frac13}\right) + \left(\cancel{\frac13}-\frac14\right) = 1 - \frac14 \end{eqnarray*} \]
In most cases (apart from telescoping series and the geometric series introduced below), there is no simple formula like Eq.(2) for the partial sum \(S_N\) Therefore, we shall develop techniques that do not rely on formulas for \(S_N\)
In general, \[ \begin{equation*} S_N =\left( \frac11 - \cancel{\frac12}\right) +\left( \cancel{\frac12} - \cancel{\frac13}\right) +\cdots + \left(\cancel{\frac1N}-\frac1{N+1}\right) = 1 - \frac1{N+1} \tag {2} \end{equation*} \]
The sum \(S\) is the limit of the partial sums: \[ S = \lim_{N\to\infty}S_N = \lim_{N\to\infty} \left(1 - \frac1{N+1}\right) = 1 \]
It is important to keep in mind the difference between a sequence \(\{a_n\}\) and an infinite series \(\sum\limits_{n=1}^{\infty}a_n\).
EXAMPLE 2 Sequences versus Series
Discuss the difference between \(\{a_n\}\) and \(\sum\limits_{n=1}^{\infty}a_n\), where \(a_n = \frac{1}{n(n+1)}\).
Make sure you understand the difference between sequences and series.
- With a sequence, we consider the limit of the individual terms \(a_n\)
- With a series, we are interested in the sum of the terms \[ a_1+a_2+a_3+\cdots \] which is defined as the limit of the partial sums.
Solution The sequence is the list of numbers \({\frac1{1(2)}, \frac1{2(3)}, \frac1{3(4)},\ldots.}\) This sequence converges to zero: \[ \lim_{n\to \infty} a_n = \lim_{n\to \infty} \frac{1}{n(n+1)} = 0 \]
The infinite series is the sum of the numbers \(a_n\) defined formally as the limit of the partial sums. This sum is not zero. In fact, the sum is equal to 1 by Example 1: \[ \sum\limits_{n=1}^{\infty}a_n = \sum_{n=1}^\infty\,\frac1{n(n+1)} = \frac1{1(2)}+\frac1{2(3)}+\frac1{3(4)}+\cdots = 1 \]
The next theorem shows that infinite series may be added or subtracted like ordinary sums, provided that the series converge.
551
THEOREM 1 Linearity of Infinite Series
If, \(\sum a_n\) and \(\sum b_n\) converge, then \(\sum (a_n \pm b_n)\) and \(\sum ca_n\) also converge (\(c\) any constant), and \[\begin{array}{*{20}{c}} \begin{align*} {\sum {a_n} + \sum {b_n}}{=}&{\sum ({a_n} + {b_n})} \\ {\sum {a_n} - \sum {b_n}}{=}&{\sum ({a_n} - {b_n})} \\ {\sum c{a_n}}{=}&{c\sum {a_n}\;\;\;(c~\textrm{any onstant})} \\ \end{align*}\end{array}\]
Proof
These rules follow from the corresponding linearity rules for limits. For example, \[\begin{array}{*{20}{c}} {\mathop \sum \limits_{n = 1}^\infty ({a_n} + {b_n})} & = & {\mathop {\lim }\limits_{N \to \infty } \mathop \sum \limits_{n = 1}^\infty ({a_n} + {b_n}) = \mathop {\lim }\limits_{N \to \infty } \left( {\mathop \sum \limits_{n = 1}^N {a_n} + \mathop \sum \limits_{n = 1}^N {b_n}} \right)} \\ {} & = & {\mathop {\lim }\limits_{N \to \infty } \mathop \sum \limits_{n = 1}^\infty {a_n} + \mathop {\lim }\limits_{N \to \infty } \mathop \sum \limits_{n = 1}^\infty {b_n} = \mathop \sum \limits_{n = 1}^\infty {a_n} + \mathop \sum \limits_{n = 1}^\infty {b_n}} \\ \end{array}\]
A main goal in this chapter is to develop techniques for determining whether a series converges or diverges. It is easy to give examples of series that diverge:
- \(S = \sum\limits_{n=1}^{\infty} 1\) diverges to infinity (the partial sums increase without bound): \[ S_1=1,\quad S_2=1+1=2,\quad S_3=1+1+1=3,\quad S_4 = 1+1+1+1=4,\quad\dots \]
- \(\sum\limits_{n=1}^{\infty} (-1)^{n-1}\) diverges (the partial sums jump between 1 and 0): \[ S_1=1,\quad S_2=1-1=0,\quad S_3=1-1+1=1,\quad S_4 = 1-1+1-1=0,\quad\dots \]
Next, we study the geometric series, which converge or diverge depending on the common ratio \(r\)
A geometric series with common ratio \(r\ne 0\) is a series defined by a geometric sequence \(cr^n\) where \(c\ne 0\) If the series begins at \(n=0\) then \[ S = \sum_{n=0}^{\infty} cr^n = c + cr + cr^2 + cr^3 + cr^4+cr^5 + \cdots \]
For \(r=\frac12\) and \(c=1\) we can visualize the geometric series starting at \(n=1\) (Figure 10.13): \[ S = \sum_{n=1}^\infty \frac1{2^n} = \frac12+\frac14+\frac18+\frac1{16}+\cdots =1 \]
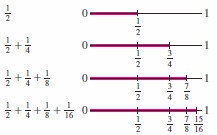
Adding up the terms corresponds to moving stepwise from 0 to 1, where each step is a move to the right by half of the remaining distance. Thus \(S=1\).
There is a simple device for computing the partial sums of a geometric series: \[ \begin{align*} S_N &\,=\, c + cr + cr^2 + cr^3 + \cdots + cr^N\\ rS_N &\,=\, cr + cr^2 + cr^3 + \cdots + cr^N + cr^{N+1}\\ S_N - rS_N &\,=\,c - cr^{N+1}\\ S_N(1-r)&\,=\, c(1-r^{N+1}) \end{align*} \]
552
If \(r\ne 1\) we may divide by \((1-r)\) to obtain \[\begin{equation*} \boxed{\bbox[#FAF8ED,5pt]{S_N = c + cr + cr^2 + cr^3 + \cdots + cr^N = \frac{c(1 - r^{N+1})}{1 - r}}} \tag{3} \end{equation*} \] This formula enables us to sum the geometric series.
Geometric series are important because they
- arise often in applications.
- can be evaluated explicitly.
- are used to study other, nongeometric series (by comparison).
THEOREM 2 Sum of a Geometric Series
Let \(c\neq 0\) If \(|r|<1\) then \[ \begin{eqnarray*} \boxed{\bbox[#FAF8ED,5pt]{\sum\limits_{n=0}^\infty cr^n = c+cr+cr^2+cr^3+\cdots = \frac{c}{1-r} }}\tag{4}\\ \boxed{\bbox[#FAF8ED,5pt]{\sum\limits_{n=M}^\infty cr^n = cr^M+cr^{M+1}+cr^{M+2}+cr^{M+3} +\cdots = \frac{cr^M}{1-r} }}\tag{5} \end{eqnarray*} \] If \(|r|\ge 1\) then the geometric series diverges.
Proof
If \(r=1\) then the series certainly diverges because the partial sums \(S_N=N\!c\) grow arbitrarily large. If \(r\neq 1\) then Eq. (3) yields \[ S = \lim_{N\to\infty} S_N = \lim_{N\to\infty} \frac{c(1 - r^{N+1})}{1 - r} = \frac{c}{1 - r} - \frac{c}{1 - r} \lim_{N\to\infty} r^{N+1} \]
If \(|r|<1\) then, \(\lim\limits_{N\to\infty}r^{N+1}=0\) and we obtain Eq (4). If \(|r|\geq 1\) and \(r\neq1\) then \(\lim\limits_{N\to\infty}r^{N+1}\) does not exist and the geometric series diverges. Finally, if the series starts with \(cr^M\) rather than \(cr^0\) then \[ \begin{equation*} S = cr^M + cr^{M + 1} + cr^{M + 2} + cr^{M + 3} + \cdots = r^M\smash{\sum_{n = 0}^\infty cr^n = \frac{cr^M}{1-r}} \end{equation*} \]
EXAMPLE 3
Evaluate \(\sum\limits_{n=0}^{\infty} 5^{-n}\).
Solution This is a geometric series with \(r=5^{-1}\) By Eq.(4), \[ \sum_{n=0}^{\infty} 5^{-n} = 1 + \frac15 + \frac1{5^2}+ \frac1{5^3} + \cdots = \frac1{1-5^{-1}} = \frac54 \]
EXAMPLE 4
Evaluate \(\sum\limits_{n=3}^{\infty} 7\left(-\frac{3}{4}\right)^n= 7\left(-\dfrac{3}{4}\right)^3 + 7\left(-\dfrac{3}{4}\right)^4 + 7\left(-\dfrac{3}{4}\right)^5 + \cdots\).
Solution This is a geometric series with \(r=-\tfrac34\) and \(c=7\) starting at \(n=3\) By Eq. (5) , \[ \sum_{n=3}^{\infty}7\left(-\dfrac{3}{4}\right)^n = \frac{7\bigl(-\frac{3}{4}\bigr)^3}{1 - \bigl(-\frac34\bigr)} = -\frac{27}{16} \]
553
EXAMPLE 5
Evaluate \(\displaystyle S = \sum_{n = 0}^{\infty} \frac{2 + 3^n}{5^{n}}.\)
Solution Write \(S\) as a sum of two geometric series. This is valid by Theorem 1 because both geometric series converge: \[ \begin{align*} \sum_{n = 0}^{\infty} \frac{2 + 3^n}{5^n} &= \sum_{n = 0}^{\infty} \frac{2}{5^n} + \sum_{n = 0}^{\infty} \frac{3^n}{5^n} = \overbrace{2\sum_{n = 0}^{\infty} \frac{1}{5^n} + \sum_{n = 0}^{\infty} \left(\frac{3}{5}\right)^n}^{\textrm{Both geometric series converge}}\\ &= 2\cdot \frac{1}{1 - \frac{1}{5}} + \frac{1}{1 - \frac{3}{5}} = 5 \end{align*} \]
GRAPHICAL INSIGHT
Sometimes, the following incorrect argument is given for summing a geometric series: \[ \begin{eqnarray*} S &=& \phantom{1+{}} \frac12+\frac14+\frac18+\cdots\\ 2S &=& 1+\frac12+\frac14+\frac18+\cdots = 1+S \end{eqnarray*} \]
Thus, \(2S=1+S\) or \(S=1\) The answer is correct, so why is the argument wrong? It is wrong because we do not know in advance that the series converges. Observe what happens when this argument is applied to a divergent series: \[ \begin{eqnarray*} S &=& 1+2+4+8+16+\cdots \\ 2S &=& \phantom{1+{}} 2+4+8+16+\cdots = S-1 \end{eqnarray*} \]
This would yield \(2S=S-1\) or \(S=-1\) which is absurd because \(S\) diverges. We avoid such erroneous conclusions by carefully defining the sum of an infinite series as the limit of partial sums.
The infinite series \(\sum\limits_{k=1}^{\infty} 1\) diverges because the \(N\) th partial sum \(S_N=N\) diverges to infinity. It is less clear whether the following series converges or diverges: \[ \sum_{n=1}^\infty (-1)^{n+1}\frac{n}{n+1} = \frac12-\frac23+\frac34-\frac45+\frac56- \cdots \]
We now introduce a useful test that allows us to conclude that this series diverges.
THEOREM 3 Divergence Test
If the \(n\) th term \(a_n\) does not converge to zero, then the series \(\sum\limits_{n=1}^\infty a_n\) diverges.
The Divergence Test (also called the nth-Term Test) is often stated as follows: \[ If \sum_{n=1}^\infty a_n~converges,~then \lim_{n\to\infty}a_n =0. \]
In practice, we use it to prove that a given series diverges.
Proof
First, note that \(a_n = S_n - S_{n-1}\) because \[ S_{n} = \big(a_1+a_2+\cdots +a_{n-1}\big)+a_n = S_{n-1} + a_n \]
554
If \(\sum\limits_{n=1}^\infty a_n\) converges with sum \(S\) then \[ \lim_{n\to\infty}a_n = \lim_{n\to\infty}(S_n-S_{n-1}) = \lim_{n\to\infty}S_n - \lim_{n\to\infty}S_{n-1}=S-S=0 \]
Therefore, if \(a_n\) does not converge to zero, \(\sum\limits^\infty_{n=1} a_n\) cannot converge.
EXAMPLE 6
Prove the divergence of \(S = \sum\limits_{n=1}^\infty \frac{n}{4n+1}\).
Solution We have \[ \lim_{n\to\infty}a_n = \lim_{n\to\infty} \frac{n}{4n+1} = \lim_{n\to\infty} \frac{1}{4+1/n} =\frac14 \]
The nth term \(a_n\) does not converge to zero, so the series diverges by Theorem 3.
EXAMPLE 7
Determine the convergence or divergence of \[ S = \sum_{n=1}^\infty (-1)^{n-1} \frac{n}{n+1} = \frac12 - \frac23 + \frac34 - \frac45 + \,\cdots \]
Solution The general term \(a_n = (-1)^{n-1} \frac{n}{n+1}\) does not approach a limit. Indeed, \(\frac{n}{n+1}\) tends to \(1\) so the odd terms \(a_{2n+1}\) tend to \(1\) and the even terms \(a_{2n}\) tend to \(-1\) Because \(\lim\limits_{n\to\infty}a_n\) does not exist, the series \(S\) diverges by Theorem 3.
The Divergence Test tells only part of the story. If \(a_n\) does not tend to zero, then \(\sum a_n\) certainly diverges. But what if \(a_n\) does tend to zero? In this case, the series may converge or it may diverge. In other words, \(\lim\limits_{n\to\infty}a_n=0\) is a necessary condition of convergence, but it is not sufficient. As we show in the next example, it is possible for a series to diverge even though its terms tend to zero.
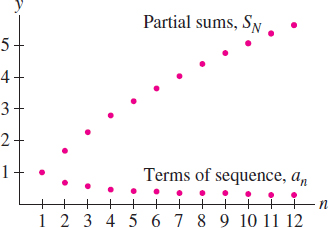
EXAMPLE 8 Sequence Tends to Zero, yet the Series Diverges
Prove the divergence of \[ \sum\limits_{n=1}^\infty \frac1{\sqrt{n}} = \frac1{\sqrt 1} +\frac1{\sqrt 2}+\frac1{\sqrt 3}+\cdots \]
Solution The general term \({1}/{\sqrt{n}}\) tends to zero. However, because each term in the partial sum \(S_N\) is greater than or equal to \(1/\sqrt{N}\) we have \[ \begin{eqnarray*} S_N &=& \overbrace{\frac1{\sqrt 1} +\frac1{\sqrt 2}+ \cdots + \frac1{\sqrt N}}^{\textrm{\(N\) terms}}\\ &\ge& \frac1{\sqrt N} +\frac1{\sqrt N} + \cdots + \frac1{\sqrt N} \\&=& N\left(\frac{1}{\sqrt N}\right) = \sqrt{N} \end{eqnarray*} \]
This shows that \(S_N\ge \sqrt N\) But \(\sqrt{N}\) increases without bound (Figure 10.14). Therefore \(S_N\) also increases without bound. This proves that the series diverges.
555
HISTORICAL PERSPECTIVE

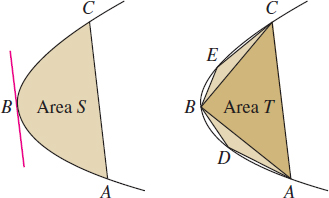
Geometric series were used as early as the third century BCE by Archimedes in a brilliant argument for determining the area \(S\) of a “parabolic segment” (shaded region in Figure 10.15). Given two points \(A\) and \(C\) on a parabola, there is a point \(B\) between \(A\) and \(C\) where the tangent line is parallel to \(\overline{AC}\) (apparently, Archimedes knew the Mean Value Theorem more than \(2000\) years before the invention of calculus). Let \(T\) be the area of triangle \(\triangle ABC\) Archimedes proved that if \(D\) is chosen in a similar fashion relative to \(\overline{AB}\) and \(E\) is chosen relative to \(\overline{BC}\) then \[ \begin{eqnarray*} \frac14 T &=& \textrm{Area}(\triangle ADB) + \textrm{Area}(\triangle BEC)\tag {6} \end{eqnarray*} \]
This construction of triangles can be continued. The next step would be to construct the four triangles on the segments \(\overline{AD}\) \(\overline{DB}\) \(\overline{BE}\) \(\overline{EC}\) of total area \(\frac14^2T\) Then construct eight triangles of total area \(\frac14^3T\) etc. In this way, we obtain infinitely many triangles that completely fill up the parabolic segment. By the formula for the sum of a geometric series, \[ S = T + \frac14T+\frac{1}{16}T + \cdots = T\sum_{n=0}^\infty \frac1{4^n} = \frac43 T \]
For this and many other achievements, Archi-medes is ranked together with Newton and Gauss as one of the greatest scientists of all time.
The modern study of infinite series began in the seventeenth century with Newton, Leibniz, and their contemporaries. The divergence of \(\sum\limits_{n=1}^\infty 1/n\) (called the harmonic series) was known to the medieval scholar Nicole d’Oresme (1323–1382), but his proof was lost for centuries, and the result was rediscovered on more than one occasion. It was also known that the sum of the reciprocal squares \( \sum\limits_{n=1}^\infty 1/{n^2}\) converges, and in the 1640s, the Italian Pietro Mengoli put forward the challenge of finding its sum. Despite the efforts of the best mathematicians of the day, including Leibniz and the Bernoulli brothers Jakob and Johann, the problem resisted solution for nearly a century. In 1735, the great master Leonhard Euler (at the time, 28 years old) astonished his contemporaries by proving that \[ \begin{equation*} \boxed{\bbox[#FAF8ED,5pt]{\frac{1}{{{1^2}}} + \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + \frac{1}{{{5^2}}} + \cdots = \frac{{{\pi ^2}}}{6}}}\end{equation*}\]
This formula, surprising in itself, plays a role in a variety of mathematical fields. A theorem from number theory states that two whole numbers, chosen randomly, have no common factor with probability \(6/\pi^2\approx 0.6\) (the reciprocal of Euler’s result). On the other hand, Euler’s result and its generalizations appear in the field of statistical mechanics.
Archimedes (287 BCE–212 BCE), who discovered the law of the lever, said “Give me a place to stand on, and I can move the earth” (quoted by Pappus of Alexandria c. AD 340).
10.2.1 Summary
- An infinite series is an expression \[ \sum_{n=1}^\infty a_n = a_1 + a_2 + a_3 + a_4 + \cdots \] We call \(a_n\) the general term of the series. An infinite series can begin at \(n=k\) for any integer \(k\).
- The \(N\) th partial sum is the finite sum of the terms up to and including the \(N\) th term: \[ S_N = \sum_{n=1}^N a_n = a_1 + a_2 + a_3 + \cdots + a_N \]
- By definition, the sum of an infinite series is the limit \(S = \lim\limits_{N\to\infty} S_N\).
If the limit exists, we say that the infinite series is
convergent or converges to the sum \(S\). If the
limit does not exist, we say that the infinite series
diverges.
556
- If the partial sums \(S_N\) increase without bound, we say that \(S\) diverges to infinity.
- Divergence Test: If \(\{a_n\}\) does not tend to zero, then \(\sum\limits_{n=1}^\infty a_n\) diverges. However, a series may diverge even if its general term \(\{a_n\}\) tends to zero.
- Partial sum of a geometric series: \[ c + cr + cr^2 + cr^3 + \cdots + cr^N = \frac{c\bigl(1 - r^{N+1}\bigr)}{1 - r} \]
- Geometric series: If \(|r|<1\) then \[ \begin{align*} \sum_{n=0}^\infty r^n &= 1 + r+r^{2}+r^{3}+\cdots = \frac{1}{1 - r}\\ \sum_{n=M}^\infty cr^n &= cr^M+cr^{M+1}+cr^{M+2}+\cdots = \frac{cr^M}{1 - r} \end{align*} \] The geometric series diverges if \(|r| \ge 1\).