10.3 Convergence of Series with Positive Terms
The next three sections develop techniques for determining whether an infinite series converges or diverges. This is easier than finding the sum of an infinite series, which is possible only in special cases.
In this section, we consider positive series \(\displaystyle\sum a_n\), where \(a_n > 0\) for all \(n\). We can visualize the terms of a positive series as rectangles of width 1 and height \(a_n\) (Figure 10.16). The partial sum \[ S_N = a_1 + a_2 + \cdots + a_N \] is equal to the area of the first \(N\) rectangles.
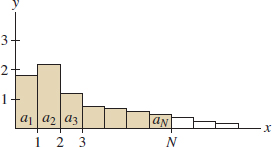
The key feature of positive series is that their partial sums form an increasing sequence: \[ S_N < S_{N+1} \] for all \(N\). This is because \(S_{N+1}\) is obtained from \(S_{N}\) by adding a positive number: \[ S_{N+1} = \bigl(a_1 + a_2 + \cdots + a_{N}\bigr) + a_{N+1} = S_{N} + \underbrace{a_{N+1}}_{\textrm{Positive}} \] Recall that an increasing sequence converges if it is bounded above. Otherwise, it diverges (Theorem 6, Section 10.1.1). It follows that a positive series behaves in one of two ways (this is the dichotomy referred to in the next theorem).
560
- Theorem 1 remains true if \(a_n\ge 0\). It is not necessary to assume that \(a_n>0\).
- It also remains true if \(a_n >0\) for all \(n\ge M\) for some \(M\), because the convergence of a series is not affected by the first \(M\) terms.
THEOREM 1 Dichotomy for Positive Series
If \(\displaystyle S=\sum_{n=1}^\infty a_n\) is a positive series, then either:
- The partial sums \(S_N\) are bounded above. In this case, \(S\) converges. Or,
- The partial sums \(S_N\) are not bounded above. In this case, \(S\) diverges.
Assumptions Matter The dichotomy does not hold for nonpositive series. Consider \[ S=\sum_{n=1}^\infty (-1)^{n-1} = 1 - 1 + 1 - 1 + 1 - 1 + \cdots \] The partial sums are bounded (because \(S_N=1\) or \(0\)), but \(S\) diverges.
Our first application of Theorem 1 is the following Integral Test. It is extremely useful because integrals are easier to evaluate than series in most cases.
The Integral Test is valid for any series \(\displaystyle\sum^\infty_{n=K} f(n)\), provided that for some \(M>0\), \(f(x)\) is positive, decreasing, and continuous for \(x\ge M\). The convergence of the series is determined by the convergence of \[ \int_M^{\infty}~f(x)\, dx \]
THEOREM 2 Integral Test
Let \(a_n = f(n)\), where \(f(x)\) is positive, decreasing, and continuous for \(x\ge 1\).
- If \(\displaystyle\int_1^{\infty} f(x)\, dx\) converges, then \(\displaystyle\sum^\infty_{n=1} a_n\) converges.
- If \(\displaystyle\int_1^{\infty} f(x)\, dx\) diverges, then \(\displaystyle\sum^\infty_{n=1} a_n\) diverges.
Proof
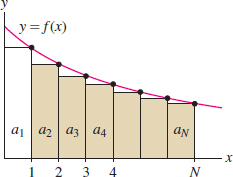
Because \(f(x)\) is decreasing, the shaded rectangles in Figure 10.17 lie below the graph of \(f(x)\), and therefore for all \(N\) \[ \underbrace{a_2 + \cdots +a_N}_{\textrm{Area of shaded rectangles in Figure 2}} \le \int_1^{N}f(x)\,dx\le \int_1^{\infty} f(x)\, dx \]
If the improper integral on the right converges, then the sums \(a_2 + \cdots + a_N\) remain bounded. In this case, \(S_N\) also remains bounded, and the infinite series converges by the Dichotomy Theorem (Theorem 1). This proves (i).
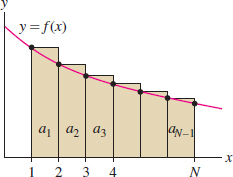
On the other hand, the rectangles in Figure 10.18 lie above the graph of \(f(x)\), so \[ \begin{equation*} \int_1^N f(x)\,dx\le \underbrace{a_1 + a_2 + \cdots + a_{N-1}}_{\textrm{Area of shaded rectangles in Figure 3}}\tag {1} \end{equation*} \] If \(\displaystyle\sum^\infty_{n=1} f(x)\, dx\) diverges, then \({\int_1^N f(x)\,dx}\) tends to \(\infty\), and Eq. (1) shows that \( S_N\) also tends to \(\infty\). This proves (ii).
561
EXAMPLE 1 The Harmonic Series Diverges
Show that \(\displaystyle\sum^\infty_{n=1} \frac1n\) diverges.
The infinite series \[ \sum_{n = 1}^\infty \frac1n \] is called the “harmonic series.”
Solution Let \(f(x)=\tfrac1x\). Then \(f(n) = \frac1n\), and the Integral Test applies because \(f\) is positive, decreasing, and continuous for \(x \geq 1\). The integral diverges: \[ \int_1^{\infty} \frac{dx}x = \lim_{R\to\infty} \int_1^R \frac{dx}{x} = \lim_{R\to\infty}\ln R = \infty \] Therefore, the series \(\sum\limits_{n=1}^\infty \frac1n\) diverges.
EXAMPLE 2
Does \(\displaystyle\sum^\infty_{n=1} \dfrac{n}{(n^2 + 1)^2} = \frac{1}{2^2}+\frac{2}{5^2}+\frac{3}{10^2}+\cdots\) converge?
Solution The function \(f(x) = \frac{x}{(x^2+1)^2}\) is positive and continuous for \(x \geq 1\). It is decreasing because \(f'(x)\) is negative: \[ f'(x) = \frac{1-3x^2}{(x^2+1)^3} <0\qquad\textrm{for \(x\ge 1\)} \] Therefore, the Integral Test applies. Using the substitution \(u = x^2 + 1\), \(du = 2x\, dx\), we have \[ \begin{align*} \int_1^{\infty} \frac{x}{(x^2+1)^2}\, dx &= \lim_{R\to\infty} \int_1^{R} \frac{x}{(x^2+1)^2}\, dx =\lim_{R\to\infty} \frac12 \int_2^{R} \frac{du}{u^2} \\ &=\lim_{R\to\infty} \frac{-1}{2u} \bigg|_2^{R} = \lim_{R\to\infty} \left(\frac1{4} - \frac1{2R} \right) = \frac14 \end{align*} \] The integral converges. Therefore, \(\displaystyle\sum_{n=1}^{\infty} \dfrac{n}{(n^2 + 1)^2}\) also converges.
The sum of the reciprocal powers \(n^{-p}\) is called a \(p\)-series.
THEOREM 3 Convergence of \(p\)-Series
The infinite series \(\displaystyle\sum^\infty_{n=1} \frac1{n^p}\) converges if \(p>1\) and diverges otherwise.
Proof
If \(p\le 0\), then the general term \(n^{-p}\) does not tend to zero, so the series diverges. If \(p>0\), then \(f(x) = x^{-p}\) is positive and decreasing, so the Integral Test applies. According to Theorem 1 in Section 7.6, \[ \int_1^{\infty} \frac{1}{x^p}\, dx = \left\{\begin{array}{@{}l@{\qquad}l} \frac1{p-1} & \text{if } p>1\\ \infty & \text{if } p\le 1 \end{array}\right. \] Therefore, \(\displaystyle\sum^\infty_{n=1} \frac1{n^p}\) converges for \(p>1\) and diverges for \(p\le 1\).
562
Here are two examples of \(p\)-series: \[ \begin{alignat*}{3} &p=\frac13&{:}\qquad &\sum_{n=1}^\infty \frac1{\sqrt[3] n} = \frac{1}{\sqrt[3] 1} + \frac{1}{\sqrt[3] 2} + \frac{1}{\sqrt[3] 3} + \frac{1}{\sqrt[3] 4} + \cdots = \infty\quad&&\textrm{diverges}\\ &p= 2&{:}\qquad & \sum_{n=1}^\infty \frac1{n^2} = \frac11+\frac{1}{2^2}+\frac1{3^2}+\frac1{4^2}+\cdots \quad& &\textrm{converges} \end{alignat*} \]
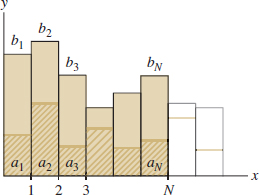
Another powerful method for determining convergence of positive series is comparison. Suppose that \(0 \leq a_n\leq b_n\). Figure 10.19 suggests that if the larger sum \(\displaystyle\sum b_n\) converges, then the smaller sum \(\displaystyle\sum a_n\) also converges. Similarly, if the smaller sum diverges, then the larger sum also diverges.
THEOREM 4 Comparison Test
Assume that there exists \(M>0\) such that \(0 \leq a_n \leq b_n\) for \(n \geq M\).
- If \(\displaystyle\sum^\infty_{n=1} b_n\) converges, then \(\displaystyle\sum^\infty_{n=1} a_n\) also converges.
- If \(\displaystyle\sum^\infty_{n=1} a_n\) diverges, then \(\displaystyle\sum^\infty_{n=1} b_n\) also diverges.
Proof
We can assume, without loss of generality, that \(M=1\). If \(\displaystyle\sum^\infty_{n=1} b_n\) converges, then the partial sums of \(\displaystyle\sum^\infty_{n=1} a_n\) are bounded above by \(S\) because \[ \begin{equation*} a_1 + a_2 + \cdots + a_N \le b_1+b_2+\cdots +b_N \le \sum_{n = 1}^{\infty} b_n = S\tag{2} \end{equation*} \] Therefore, \(\sum\limits_{n=1}^\infty a_n\) converges by the Dichotomy Theorem (Theorem 1). This proves (i). On the other hand, if \(\displaystyle\sum^\infty_{n=1} a_n\) diverges, then \(\displaystyle\sum^\infty_{n=1} b_n\) must also diverge. Otherwise we would have a contradiction to (i).
EXAMPLE 3
Does \(\displaystyle\sum^\infty_{n=1} \frac{1}{\sqrt{n}\,3^n}\) converge?
Solution For \(n\ge 1\), we have \[ \frac{1}{\sqrt{n}\,3^n} \le \frac{1}{3^n} \] The larger series \(\displaystyle\sum^\infty_{n=1} \frac{1}{3^{n}}\) converges because it is a geometric series with \({r=\frac13<1}\). By the Comparison Test, the smaller series \(\displaystyle\sum^\infty_{n=1} \frac{1}{\sqrt{n}\,3^n}\) also converges.
In words, the Comparison Test states that for positive series:
- Convergence of the larger series forces convergence of the smaller series.
- Divergence of the smaller series forces divergence of the larger series.
563
EXAMPLE 4
Does \(\displaystyle\sum^\infty_{n=1} \frac1{(n^2+3)^{1/3}}\) converge?
Solution Let us show that \[ \frac{1}{n}\le \frac1{(n^2+3)^{1/3}} \qquad\textrm{for \(n\ge 2\)} \] This inequality is equivalent to \((n^2+3)\le n^3\), so we must show that \[f(x) = x^3-(x^2+3)\ge 0 \qquad\textrm{for \(x\ge 2\)}\] The function \(f(x)\) is increasing because its derivative \(f'(x) = 3x\big(x-\frac23\big)\) is positive for \(x\ge 2\). Since \(f(2)=1\), it follows that \(f(x)\ge 1\) for \(x\ge 2\), and our original inequality follows. We know that the smaller harmonic series \(\displaystyle\sum^\infty_{n=2} \frac{1}{n}\) diverges. Therefore, the larger series \(\displaystyle\sum^\infty_{n=2} \frac{1}{(n^2+1)^{1/3}}\) also diverges.
EXAMPLE 5 Using the Comparison Correctly
Study the convergence of \[ \sum_{n = 2}^{\infty} \frac{1}{n(\ln n)^2} \]
Solution We might be tempted to compare \(\displaystyle\sum^\infty_{n=2} \frac{1}{n(\ln n)^2}\) to the harmonic series \(\displaystyle\sum^\infty_{n=2} \frac{1}{n}\) using the inequality (valid for \(n \geq 3\)) \[ \frac1{n(\ln n)^2}\le \frac1n \] However, \(\displaystyle\sum^\infty_{n=2} \frac{1}{n}\) diverges, and this says nothing about the smaller series \(\sum \frac{1}{n(\ln n)^2}\). Fortunately, the Integral Test can be used. The substitution \(u = \ln x\) yields \[ \int_2^\infty \frac{dx}{x(\ln x)^2} = \int_{\ln 2}^\infty\frac{du}{u^2} = \lim_{R\to\infty} \left(\frac1{\ln 2} -\frac1{R} \right) = \frac1{\ln 2} <\infty \] The Integral Test shows that \(\displaystyle\sum^\infty_{n=2} \frac{1}{n(\ln n)^2}\) converges.
Suppose we wish to study the convergence of \[ S=\sum_{n = 2}^{\infty} \frac{n^2}{n^4 - n-1} \]
For large \(n\), the general term is very close to \({1}/{n^2}\): \[ \frac{n^2}{n^4 - n-1} = \frac{1}{n^2-n^{-1}-n^{-2}} \approx \frac1{n^2} \]
564
Thus we might try to compare \(S\) with \(\displaystyle\sum^\infty_{n=2} \frac{1}{n^2}\). Unfortunately, however, the inequality goes in the wrong direction: \[ \frac{n^2}{n^4 - n-1} > \frac{n^2}{n^4} = \frac1{n^2} \] Although the smaller series \(\displaystyle\sum^\infty_{n=2} \frac{1}{n^2}\) converges, we cannot use the Comparison Theorem to say anything about our larger series. In this situation, the following variation of the Comparison Test can be used.
THEOREM 5 Limit Comparison Test
Let \(\{a_n\}\) and \(\{b_n\}\) be positive sequences. Assume that the following limit exists: \[ L = \lim\limits_{n\to\infty}\frac{a_n}{b_n} \]
- If \(L > 0\), then \({\displaystyle\sum a_n}\) converges if and only if \({\displaystyle\sum b_n}\) converges.
- If \(L=\infty\) and \({\displaystyle\sum a_n}\) converges, then \({\displaystyle\sum b_n}\) converges.
- If \(L = 0\) and \({\displaystyle\sum b_n}\) converges, then \({\displaystyle\sum a_n}\) converges.
CAUTION
The Limit Comparison Test is not valid if the series are not positive. See Exercise 44 in Section 10.4.
Proof
Assume first that \(L\) is finite (possibly zero) and that \(\displaystyle\sum b_n\) converges. Choose a positive number \(R > L\). Then \(0 \leq a_n/b_n \leq R\) for all \(n\) sufficiently large because \(a_n/b_n\) approaches \(L\). Therefore \(a_n \leq Rb_n\). The series \(\displaystyle\sum Rb_n\) converges because it is a multiple of the convergent series \(\displaystyle\sum b_n\). Therefore \(\sum a_n\) converges by the Comparison Test.
Next, suppose that \(L\) is nonzero (positive or infinite) and that \(\sum a_n\) converges. Let \(L^{-1} = \lim_{n\to\infty} {b_n}/{a_n}\). Then \(L^{-1}\) is finite and we can apply the result of the previous paragraph with the roles of \(\{a_n\}\) and \(\{b_n\}\) reversed to conclude that \({\displaystyle\sum b_n}\) converges.
CONCEPTUAL INSIGHT
To remember the different cases of the Limit Comparison Test, you can think of it this way. If \(L>0\), then \(a_n\approx Lb_n\) for large \(n\). In other words, the series \({\displaystyle\sum a_n}\) and \({\displaystyle\sum b_n}\) are roughly multiples of each other, so one converges if and only if the other converges. If \(L=\infty\), then \(a_n\) is much larger than \(b_n\) (for large \(n\)), so if \({\displaystyle\sum a_n}\) converges, \({\displaystyle\sum b_n}\) certainly converges. Finally, if \(L=0\), then \(b_n\) is much larger than \(a_n\) and the convergence of \({\displaystyle\sum b_n}\) yields the convergence of \(\sum a_n\).
EXAMPLE 6
Show that \(\displaystyle\sum^\infty_{n=2} \frac{n^2}{n^4 - n-1}\) converges.
Solution Let \[{a_n ={\frac{n^2}{n^4 - n-1}}}\quad \text{and}\quad {b_n = \frac{1}{{n^{2}}}}\]
565
We observed above that \(a_n\approx b_n\) for large \(n\). To apply the Limit Comparison Test, we observe that the limit \(L\) exists and \(L>0\): \[ \begin{eqnarray*} L &=& \lim_{n\to \infty}\frac{a_n}{b_n} = \lim_{n\to \infty}\frac{n^2}{n^4 -n -1}\cdot\frac{n^2}{1} = \lim_{n\to \infty} \frac{1}{1 - n^{-3}-n^{-4}} =1 \end{eqnarray*} \]
Since \(\displaystyle\sum^\infty_{n=2} \frac1{n^2}\) converges, our series \(\displaystyle\sum^\infty_{n=2} \frac{n^2}{n^4 - n-1}\) also converges by Theorem 5.
EXAMPLE 7
Determine whether \(\displaystyle\sum^\infty_{n=3} \frac{1}{\sqrt{n^2+4}}\) converges.
Solution Apply the Limit Comparison Test with \(a_n = \frac{1}{\sqrt{n^2+4}}\) and \(b_n = \frac1n\). Then \[ L = \lim_{n\to\infty}\frac{a_n}{b_n} = \lim_{n\to\infty}\frac{n}{\sqrt{n^2+4}} = \lim_{n\to\infty}\frac1{\sqrt{1+4/n^2}} = 1 \] Since \(\displaystyle\sum^\infty_{n=3} \frac1n\) diverges and \(L > 0\), the series \(\displaystyle\sum^\infty_{n=3} \frac{1}{\sqrt{n^2+4}}\) also diverges.
10.3.1 Summary
- The partial sums \(S_N\) of a positive series \(\displaystyle S=\sum a_n\) form an increasing sequence.
- Dichotomy Theorem: A positive series \(S\) converges if its partial sums \(S_N\) remain bounded. Otherwise, it diverges.
- Integral Test: Assume that \(f\) is positive, decreasing, and continuous for \(x>M\). Set \(a_n = f(n)\). If \(\int_M^{\infty} f(x)\, dx\) converges, then \(\displaystyle S=\sum a_n\) converges, and if \( \int_M^{\infty} f(x)\, dx\) diverges, then \(\displaystyle S=\sum a_n\) diverges.
- \(p\)-Series: The series \({\displaystyle\sum_{n=1}^{\infty} \frac{1}{n^p}}\) converges if \(p > 1\) and diverges if \(p \leq 1\).
- Comparison Test: Assume there exists \(M>0\) such that \(0 \leq a_n \leq b_n\) for all \(n \geq M\). If \({\displaystyle\sum b_n}\) converges, then \({\displaystyle\sum a_n}\) converges, and if \({\displaystyle\sum a_n}\) diverges, then \({\displaystyle\sum b_n}\) diverges.
- Limit Comparison Test: Assume that \(\{a_n\}\) and \(\{b_n\}\) are positive and that the following limit exists: \[ L = \lim_{n\to\infty} \frac{a_n}{b_n} \]
- - If \(L > 0\), then \(\sum a_n\) converges if and only if \(\sum b_n\) converges.
- - If \(L=\infty\) and \(\sum a_n\) converges, then \(\sum b_n\) converges.
- - If \(L = 0\) and \(\sum b_n\) converges, then \(\sum a_n\) converges.
566