10.4 Absolute and Conditional Convergence

In the previous section, we studied positive series, but we still lack the tools to analyze series with both positive and negative terms. One of the keys to understanding such series is the concept of absolute convergence.

DEFINITION Absolute Convergence

The series \(\sum a_n\) converges absolutely if \(\sum |a_n|\) converges.

EXAMPLE 1

Verify that the series \[ \sum_{n=1}^\infty\frac{(-1)^{n-1}}{n^2} = \frac1{1^2} - \frac1{2^2}+\frac1{3^2}-\frac1{4^2}+\cdots \] converges absolutely.

Solution This series converges absolutely because the positive series (with absolute values) is a \(p\)-series with \(p=2>1\): \[ \sum_{n=1}^\infty\,\Big|\frac{(-1)^{n-1}}{n^2}\Big| = \frac1{1^2} + \frac1{2^2}+\frac1{3^2} + \frac1{4^2}+\cdots\qquad \textrm{(convergent \(p\)-series)} \]

The next theorem tells us that if the series of absolute values converges, then the original series also converges.

THEOREM 1 Absolute Convergence Implies Convergence

If \({\displaystyle\sum |a_n|}\) converges, then \({\displaystyle\sum a_n}\) also converges.

Proof

We have \(-|a_n|\le a_n\le |a_n|\). By adding \(|a_n|\) to all parts of the inequality, we get \(0\le |a_n|+a_n\le 2|a_n|\). If \({\displaystyle\sum |a_n|}\) converges, then \({\displaystyle\sum 2|a_n|}\) also converges, and therefore, \({\displaystyle\sum (a_n+|a_n|)}\) converges by the Comparison Test. Our original series converges because it is the difference of two convergent series: \[ \sum a_n = \sum (a_n + |a_n|) - \sum |a_n| \]

570

EXAMPLE 2

Verify that \(\displaystyle S = \sum^\infty_{n=1} \frac{(-1)^{n-1}}{n^2}\) converges.

Solution We showed that \(S\) converges absolutely in Example 1. By Theorem 1, \(S\) itself converges.

EXAMPLE 3

Does \(S = \sum\limits_{n=1}^\infty \frac{(-1)^{n-1}}{\sqrt{n}}=\frac1{\sqrt{1}}-\frac1{\sqrt{2}}+\frac1{\sqrt{3}} - \cdots \) converge absolutely?

Solution  The positive series \({\displaystyle\sum_{n=1}^\infty \frac{1}{\sqrt{n}}}\) is a \(p\)-series with \(p=\frac12\). It diverges because \(p<1\). Therefore, \(S\) does not converge absolutely.

The series in the previous example does not converge absolutely, but we still do not know whether or not it converges. A series \({\displaystyle\sum a_n}\) may converge without converging absolutely. In this case, we say that \({\displaystyle\sum a_n}\) is conditionally convergent.

DEFINITION Conditional Convergence

An infinite series \({\displaystyle\sum a_n}\) converges conditionally if \({\displaystyle\sum a_n}\) converges but \(\displaystyle\sum |a_n|\) diverges.

If a series is not absolutely convergent, how can we determine whether it is conditionally convergent? This is often a more difficult question, because we cannot use the Integral Test or the Comparison Test (they apply only to positive series). However, convergence is guaranteed in the particular case of an alternating series \[ S = \sum_{n=1}^{\infty} (-1)^{n-1} a_n = a_1 - a_2 + a_3 - a_4 + \cdots \] where the terms \(a_n\) are positive and decrease to zero (Figure 10.20).

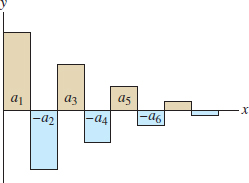
Figure 10.20: An alternating series with decreasing terms. The sum is the signed area, which is at most \(a_1\).

THEOREM 2 Leibniz Test for Alternating Series

Assume that \(\{a_n\}\) is a positive sequence that is decreasing and converges to \(0\): \[\boxed{\bbox[#FAF8ED,5pt]{ a_1 > a_2 > a_3 > a_4 > \dots > 0,\qquad \lim\limits_{n\to\infty}a_n = 0 }}\] Then the following alternating series converges: \[\boxed{\bbox[#FAF8ED,5pt]{ S = \sum\limits_{n=1}^{\infty} (-1)^{n-1} a_n = a_1 - a_2 + a_3 - a_4 + \cdots}} \] Furthermore, \[ \boxed{\bbox[#FAF8ED,5pt]{ 0< S < a_1\quad\textrm{and}\quad S_{2N}< S < S_{2N+1}\qquad N\ge 1 }} \]

Assumptions Matter

The Leibniz Test is not valid if we drop the assumption that \(a_n\) is decreasing (see Exercise 35.)

571

Proof

We will prove that the partial sums zigzag above and below the sum \(S\) as in Figure 10.21. Note first that the even partial sums are increasing. Indeed, the odd-numbered terms occur with a plus sign and thus, for example, \[ S_4 + a_5-a_6 =S_6 \] But \(a_5-a_6>0\) because \(a_n\) is decreasing, and therefore \(S_4<S_6\). In general, \[ S_{2N} + (a_{2N+1}-a_{2N+2}) =S_{2N+2} \] where \(a_{2n+1}-a_{2N+2}>0\). Thus \( S_{2N} < S_{2N+2}\) and \[ 0<S_2<S_4<S_6<\cdots \] Similarly, \[ S_{2N-1} - (a_{2N}-a_{2N+1}) =S_{2N+1} \] Therefore \(S_{2N+1} < S_{2N-1}\), and the sequence of odd partial sums is decreasing: \[ \cdots < S_7 < S_5 < S_3< S_1 \] Finally, \( S_{2N} < S_{2N}+a_{2N+1}=S_{2N+1}\). The picture is as follows: \[ 0 < S_2 < S_4< S_6 < \quad \cdots \quad < S_7< S_5 < S_3 < S_1 \] Now, because bounded monotonic sequences converge (Theorem 6 of Section 10.1.1), the even and odd partial sums approach limits that are sandwiched in the middle: \[ \begin{equation*} 0 < S_2 < S_4 < \cdots < \lim_{N\to\infty} S_{2N} \le \lim_{N\to\infty} S_{2N+1} < \cdots < S_5 < S_3 < S_1\tag{1} \end{equation*} \] These two limits must have a common value \(L\) because \[ \lim_{N\to\infty} S_{2N+1} - \lim_{N\to\infty} S_{2N} = \lim_{N\to\infty} (S_{2N+1}-S_{2N}) = \lim_{N\to\infty} a_{2N+1} = 0 \] Therefore, \(\lim\limits_{N\to\infty} S_{N} = L\) and the infinite series converges to \(S=L\). From Eq (1) we also see that \(0< S < S_1 = a_1\) and \(S_{2N}< S < S_{2N+1}\) for all \(N\) as claimed.

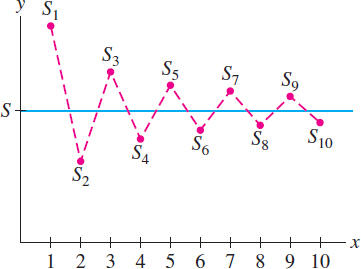
Figure 10.21: The partial sums of an alternating series zigzag above and below the limit. The odd partial sums decrease and the even partial sums increase.

EXAMPLE 4

Show that \(S = \sum\limits_{n=1}^\infty \frac{(-1)^{n-1}}{\sqrt{n}}=\frac1{\sqrt{1}}-\frac1{\sqrt{2}}+\frac1{\sqrt{3}} - \cdots \) converges conditionally and that \(0\le S \le 1\).

Solution The terms \(a_n = 1/{\sqrt n}\) are positive and decreasing, and \(\lim\limits_{n\to\infty}a_n=0\). Therefore, \(S\) converges by the Leibniz Test. Furthermore, \(0 \le S \le 1\) because \(a_1=1\). However, the positive series \({\displaystyle\sum_{n=1}^\infty 1/{\sqrt n}}\) diverges because it is a \(p\)-series with \(p=\tfrac{1}{2}<1\). Therefore, \(S\) is conditionally convergent but not absolutely convergent (Figure 10.22).

The Leibniz Test is the only test for conditional convergence developed in this text. Other tests, such as Abel’s Criterion and the Dirichlet Test, are discussed in textbooks on Analysis.

572

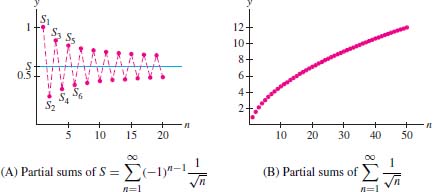
The inequality \(S_{2N}< S < S_{2N+1}\) in Theorem 2 gives us important information about the error; it tells us that \(|S_N-S|\) is less than \(|S_N-S_{N+1}| = a_{N+1}\) for all \(N\).

THEOREM 3

Let \({\displaystyle S = \sum_{n=1}^{\infty} (-1)^{n-1} a_n}\), where \(\{a_n\}\) is a positive decreasing sequence that converges to \(0\). Then \[ \begin{equation*} \boxed{\bbox[#FAF8ED,5pt]{\big| S-S_N\big| < a_{N+1}}}\tag{2} \end{equation*} \] In other words, the error committed when we approximate \(S\) by \(S_N\) is less than the size of the first omitted term \(a_{N+1}\).

EXAMPLE 5 Alternating Harmonic Series

Show that \(S = \sum\limits_{n=1}^\infty\frac{(-1)^{n-1}}n\) converges conditionally. Then:

  1. Show that \(|S-S_6| < \frac17\).
  2. Find an \(N\) such that \(S_N\) approximates \(S\) with an error less than \(10^{-3}\).

Solution The terms \(a_n = 1/n\) are positive and decreasing, and \(\lim\limits_{n\to\infty}a_n=0\). Therefore, \(S\) converges by the Leibniz Test. The harmonic series \({\displaystyle\sum_{n=1}^\infty 1/n}\) diverges, so \(S\) converges conditionally but not absolutely. Now, applying Eq (2), we have \[ \left|S - S_N \right| < a_{N+1}=\frac1{N+1} \] For \(N=6\), we obtain \(|S-S_6|< a_7 = \tfrac17\). We can make the error less than \(10^{-3}\) by choosing \(N\) so that \[\frac1{N+1}\le 10^{-3}\quad\Rightarrow\quad N+1\ge 10^3\quad\Rightarrow\quad N\ge 999 \] Using a computer algebra system, we find that \(S_{999} \approx 0.69365\). In Exercise 84 of Section 10.7, we will prove that \(S = \ln 2 \approx 0.69314\), and thus we can verify that \[|S-S_{999}|\approx |\ln 2 - 0.69365|\approx 0.0005 < 10^{-3} \]

573

CONCEPTUAL INSIGHT

The convergence of an infinite series \({\displaystyle\sum a_n}\) depends on two factors: (1) how quickly \(a_n\) tends to zero, and (2) how much cancellation takes place among the terms. Consider \begin{array}{\left*{20}{\leftc}} {{\rm{Harmonic series (diverges):}}} & {1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \cdots } \\ {p{\rm{ - Series with }}p{\rm{ = 2 (converges):}}} & {1 + \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + \frac{1}{{{5^2}}} + \cdots } \\ {{\rm{Alternating\;harmonic\;series\;(converges):}}} & {1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \ldots } \\ \end{array} The harmonic series diverges because reciprocals \( {1}/{n}\) do not tend to zero quickly enough. By contrast, the reciprocal squares \({1}/{n^2}\) tend to zero quickly enough for the \(p\)-series with \(p=2\) to converge. The alternating harmonic series converges, but only due to the cancellation among the terms.

10.4.1 Summary