10.7 Taylor Series
In this section we develop general methods for finding power series representations. Suppose that \(f(x)\) is represented by a power series centered at \(x = c\) on an interval \((c-R, c+R)\) with \(R > 0\): \[ f(x) = \sum_{n=0}^\infty a_n(x-c)^n = a_0+a_1(x-c)+a_2(x-c)^2+\cdots \] According to Theorem 2 in Section 10.6, we can compute the derivatives of \(f(x)\) by differentiating the series expansion term by term: \[ \begin{array}{@{}r@{\;}r@{\;}r@{\;}r@{\;}r@{}} f(x) =& a_0 \; +& a_1(x-c)\;+& a_2(x-c)^2 \;+& a_3(x-c)^3 +\cdots\\ f'(x) =& a_1 \; +& 2a_2(x-c)\;+& 3a_3(x-c)^2 \;+& 4a_4(x-c)^3 +\cdots\\ f''(x) =& 2a_2 \; +& 2\cdot 3a_3(x-c)\;+& 3\cdot 4a_4(x-c)^2 \;+& 4\cdot 5a_5(x-c)^3 + \cdots \\ f'''(x)=& 2\cdot3 a_3\; +& 2\cdot3\cdot4a_4(x-2)\;+& 3\cdot4\cdot5a_5(x-2)^2\; +&\;\cdots \end{array} \] In general, \[ f^{(k)}(x) = k!a_k + \Big(2\cdot 3\cdots (k+1)\Big)a_{k+1}(x-c) + \cdots \] Setting \(x=c\) in each of these series, we find that \[ f(c) = a_0,\quad f'(c) = a_1, \quad f''(c) = 2a_2,\quad f'''(c) = 2\cdot 3a_2,\quad \ldots,\quad f^{(k)}(c) = k!a_k,\quad \ldots \]
592
We see that \(a_k\) is the \(k\)th coefficient of the Taylor polynomial studied in Section 8.4: \[ \begin{equation*} \boxed{{\bbox[#FAF8ED,5pt]{a_k = \frac{f^{(k)}(c)}{k!}}}}\tag{1} \end{equation*} \] Therefore \(f(x) = T(x)\), where \(T(x)\) is the Taylor series of \(f(x)\) centered at \(x=c\): \[ T(x) = f(c)+f'(c)(x-c)+\frac{f''(c)}{2!}(x-c)^2 +\frac{f'''(c)}{3!}(x-c)^3+\cdots \] This proves the next theorem.
THEOREM 1 Taylor Series Expansion
If \(f(x)\) is represented by a power series centered at \(c\) in an interval \(|x-c|< R\) with \(R>0\), then that power series is the Taylor series \[ \boxed{\bbox[#FAF8ED,5pt]{T(x) = \sum\limits_{n=0}^\infty \frac{f^{(n)}(c)}{n!}(x-c)^n}} \]
In the special case \(c = 0\), \(T(x)\) is also called the Maclaurin series: \[ \boxed{\bbox[#FAF8ED,5pt]{f(x) = \sum\limits_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + \frac{f^{(4)}(0)}{4!}x^4 + \cdots}} \]
EXAMPLE 1
Find the Taylor series for \(f(x)=x^{-3}\) centered at \(c=1\).
Solution The derivatives of \(f(x)\) are \(f'(x)=-3x^{-4}\), \(f''(x)=(-3)(-4)x^{-5}\), and in general, \[ f^{(n)}(x) = (-1)^n(3)(4)\cdots(n+2) x^{-3-n} \]
Note that \((3)(4)\cdots(n+2) =\tfrac12 (n+2)!\). Therefore, \[f^{(n)}(1) = (-1)^n\frac12(n+2)!\] Noting that \((n+2)! = (n+2)(n+1)n!\), we write the coefficients of the Taylor series as: \[ a_n = \frac{f^{(n)}(1)}{n!}=\frac{(-1)^n\frac12(n+2)!}{n!} = (-1)^n\frac{(n+2)(n+1)}2 \]
The Taylor series for \(f(x)=x^{-3}\) centered at \(c=1\) is \[ \begin{align*} T(x) &= 1-3(x-1)+6(x-1)^2-10(x-1)^3+\cdots \\&= \sum\limits_{n=0}^\infty\,(-1)^n\frac{(n+2)(n+1)}2(x-1)^n \end{align*} \]
Theorem 1 tells us that if we want to represent a function \(f(x)\) by a power series centered at \(c\), then the only candidate for the job is the Taylor series: \[ T(x) = \sum_{n=0}^\infty \frac{f^{(n)}(c)}{n!}(x-c)^n \]
593
See Exercise 92 for an example where a Taylor series \(T(x)\) converges but does not converge to \(f(x)\).
However, there is no guarantee that \(T(x)\) converges to \(f(x)\), even if \(T(x)\) converges. To study convergence, we consider the \(k\)th partial sum, which is the Taylor polynomial of degree \(k\): \[ T_k(x) = f(c) + f'(c)(x - c) + \frac{f''(c)}{2!}(x - c)^2 + \cdots + \frac{f^{(k)}(c)}{k!}(x - c)^k \] In Section 8.4, we defined the remainder \[ R_k(x) = f(x) - T_k(x) \] Since \(T(x)\) is the limit of the partial sums \(T_k(x)\), we see that \[ The\;Taylor\;series\;converges\;to\;f(x)\;if\;and\;only\;if\;\lim\limits_{k\to\infty} R_k(x)=0. \] There is no general method for determining whether \(R_k(x)\) tends to zero, but the following theorem can be applied in some important cases.
Reminder
\(f(x)\) is called “infinitely differentiable” if \(f^{(n)}(x)\) exists for all \(n\).
THEOREM 2
Let \(I =(c-R, c+R)\), where \(R>0\). Suppose there exists \(K>0\) such that all derivatives of \(f\) are bounded by \(K\) on \(I\): \[ |f^{(k)}(x)|\le K\qquad \textrm{for all}\quad k\geq 0\quad \textrm{and}\quad x\in I \] Then \(f(x)\) is represented by its Taylor series in \(I\): \[ f(x) = \sum_{n=0}^\infty \frac{f^{(n)}(c)}{n!} (x-c)^n \qquad\textrm{for all}\quad x\in I \]
Proof
According to the Error Bound for Taylor polynomials (Theorem 2 in Section 8.4), \[ |R_k(x)|=|f(x)-T_k(x)| \le K\frac{|x-c|^{k+1}}{(k+1)!} \] If \(x \in I\), then \(|x-c|<R\) and \[ |R_k(x)| \le K\frac{R^{k+1}}{(k+1)!} \] We showed in Example 9 of Section 10.1 that \(R^k/k!\) tends to zero as \(k\to\infty\). Therefore, \(\lim\limits_{k\to\infty} R_k(x)=0\) for all \(x\in (c-R, c+R)\), as required.
Taylor expansions were studied throughout the seventeenth and eighteenth centuries by Gregory, Leibniz, Newton, Maclaurin, Taylor, Euler, and others. These developments were anticipated by the great Hindu mathematician Madhava (c. 1340–1425), who discovered the expansions of sine and cosine and many other results two centuries earlier.
EXAMPLE 2 Expansions of Sine and Cosine
Show that the following Maclaurin expansions are valid for all \(x\). \[ \boxed{\bbox[#FAF8ED,5pt]{\sin x = \sum\limits_{n=0}^{\infty} (-1)^n\frac{x^{2n+1}}{(2n+1)!} = x- \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots}} \]
594
\[ \boxed{\bbox[#FAF8ED,5pt]{\cos x = \sum\limits_{n=0}^{\infty} (-1)^n\frac{x^{2n}}{(2n)!} = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots}} \]
Solution Recall that the derivatives of \(f(x) = \sin x\) and their values at \(x=0\) form a repeating pattern of period 4:
| \(f(x)\) | \(f'(x)\) | \(f''(x)\) | \(f'''(x)\) | \(f^{(4)}(x)\) | \(\cdots\) |
| \(\sin x\) | \(\cos x\) | \(-\sin x\) | \(-\cos x\) | \(\sin x\) | \(\cdots\) |
| 0 | \(1\) | \(0\) | \(-1\) | \(0\) | \(\cdots\) |
In other words, the even derivatives are zero and the odd derivatives alternate in sign: \(f^{(2n+1)}(0) = (-1)^n\). Therefore, the nonzero Taylor coefficients for \(\sin x\) are \[a_{2n+1} = \frac{(-1)^n}{(2n+1)!}\] For \(f(x)=\cos x\), the situation is reversed. The odd derivatives are zero and the even derivatives alternate in sign: \(f^{(2n)}(0)=(-1)^n\cos 0 = (-1)^n\). Therefore the nonzero Taylor coefficients for \(\cos x\) are \({a_{2n} = {(-1)^n}/{(2n)!}}\).
We can apply Theorem 2 with \(K=1\) and any value of \(R\) because both sine and cosine satisfy \(|f^{(n)}(x)|\le 1\) for all \(x\) and \(n\). The conclusion is that the Taylor series converges to \(f(x)\) for \(\left|x\right|<R\). Since \(R\) is arbitrary, the Taylor expansions hold for all \(x\).
EXAMPLE 3 Taylor Expansion of \(f(x) = e^x\) at \(x=c\)
Find the Taylor series \(T(x)\) of \(f(x) = e^x\) at \(x=c\).
Solution We have \(f^{(n)}(c)=e^c\) for all \(x\), and thus \[ T(x) = \sum_{n=0}^\infty \frac{e^c}{n!} (x-c)^n \] Because \(e^x\) is increasing for all \(R>0\) we have \(|f^{(k)}(x)|\le e^{c+R}\) for \(x \in (c-R, c+R)\). Applying Theorem 2 with \(K=e^{c+R}\), we conclude that \(T(x)\) converges to \(f(x)\) for all \(x \in (c-R, c+R)\). Since \(R\) is arbitrary, the Taylor expansion holds for all \(x\). For \(c=0\), we obtain the standard Maclaurin series \[\boxed{\bbox[#FAF8ED,5pt]{e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots}} \]
Shortcuts to Finding Taylor Series
There are several methods for generating new Taylor series from known ones. First of all, we can differentiate and integrate Taylor series term by term within its interval of convergence, by Theorem 2 of Section #. We can also multiply two Taylor series or substitute one Taylor series into another (we omit the proofs of these facts).
EXAMPLE 4
Find the Maclaurin series for \(f(x) = x^2e^x\).
Solution Multiply the known Maclaurin series for \(e^x\) by \(x^2\). \[ \begin{eqnarray*} x^2e^x & = & x^2\left(1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \cdots\right)\\ &=& x^2 +x^3+ \frac{x^4}{2!} + \frac{x^5}{3!} + \frac{x^6}{4!} +\frac{x^7}{5!}+\cdots = \sum_{n = 2}^{\infty} \frac{x^{n}}{(n-2)!} \end{eqnarray*} \]
In Example 4, we can also write the Maclaurin series as \[ \sum_{n = 0}^{\infty} \frac{ x^{n+2} } { n! }\]
595
EXAMPLE 5 Substitution
Find the Maclaurin series for \(e^{-x^2}\).
Solution Substitute \(-x^2\) in the Maclaurin series for \(e^x\). \[ \begin{equation*} e^{-x^2}= \sum_{n=0}^\infty \frac{(-x^2)}{n!}^n = \sum_{n=0}^\infty \frac{(-1)^nx^{2n}}{n!}= 1 - x^2 + \frac{x^4}{2!} - \frac{x^6}{3!} + \frac{x^8}{4!} - \cdots\tag{2} \end{equation*} \] The Taylor expansion of \(e^x\) is valid for all \(x\), so this expansion is also valid for all \(x\).
EXAMPLE 6 Integration
Find the Maclaurin series for \(f(x) = \ln (1 + x)\).
Solution We integrate the geometric series with common ratio \(-x\) (valid for \(\left|x\right|<1\)): \[ \begin{align*} \frac1{1+x}&= 1-x+x^2-x^3+\cdots \\ \ln(1+x)&=\int\frac{dx}{1+x}= x-\frac{x^2}2+\frac{x^3}3-\frac{x^4}4+\cdots= \sum_{n=1}^{\infty} (-1)^{n-1} \frac{x^n}{n} \end{align*} \] The constant of integration on the right is zero because \(\ln(1+x) = 0\) for \(x=0\). This expansion is valid for \(\left|x\right|<1\). It also holds for \(x=1\) (see Exercise 84.)
In many cases, there is no convenient general formula for the Taylor coefficients, but we can still compute as many coefficients as desired.
EXAMPLE 7 Multiplying Taylor Series
Write out the terms up to degree five in the Maclaurin series for \(f(x) = e^x \cos x\).
Solution We multiply the fifth-order Taylor polynomials of \(e^x\) and \(\cos x\) together, dropping the terms of degree greater than 5: \[ \left(1+x +\frac{x^2}2 + \frac{x^3}6 + \frac{x^4}{24}+\frac{x^5}{120} \right)\left(1 - \frac{x^2}{2} + \frac{x^4}{24} \right) \] Distributing the term on the left (and ignoring terms of degree greater than \(5\)), we obtain \[ \begin{eqnarray*} &\displaystyle\left(1+x +\frac{x^2}2 + \frac{x^3}6 + \frac{x^4}{24}+\frac{x^5}{120} \right) - \left(1+x +\frac{x^2}2 + \frac{x^3}6\right)\left(\frac{x^2}{2}\right)+ (1+x) \left(\frac{x^4}{24}\right)&\\ &= \underbrace{ 1+x-\frac{x^3}3-\frac{x^4}6 -\frac{x^5}{30}}_{\text{Retain terms of degree \(\leq 5\)}}{}& \end{eqnarray*} \] We conclude that the fifth Maclaurin polynomial for \(f(x) = e^x \cos x\) is \[ T_5(x) = 1+x-\frac{x^3}3-\frac{x^4}6 -\frac{x^5}{30} \]
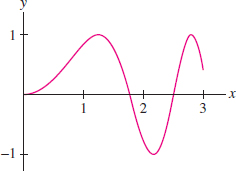
In the next example, we express the definite integral of \(\sin(x^2)\) as an infinite series. This is useful because the integral cannot be evaluated explicitly. Figure 10.28 shows the graph of the Taylor polynomial \(T_{12}(x)\) of the Taylor series expansion of the antiderivative.
EXAMPLE 8
Let \(J=\int_0^1 \sin(x^2)\,dx\).
- Express \(J\) as an infinite series.
- Determine \(J\) to within an error less than \(10^{-4}\).
596
Solution
- The Maclaurin expansion for \(\sin x\) is valid for all \(x\), so we have \[ \sin x = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}x^{2n+1}\quad \Rightarrow\quad \sin(x^2) = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}x^{4n+2} \] We obtain an infinite series for \(J\) by integration: \[ \begin{align*} J&=\int_0^1\sin(x^2)\,dx = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}\int_0^1 x^{4n+2}dx =\sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}\left(\frac1{4n+3}\right)\notag\\ &= \frac13-\frac1{42} +\frac1{1320}- \frac1{75{,}600} + \cdots\tag{3} \end{align*} \]
- The infinite series for \(J\) is an alternating series with decreasing terms, so the sum of the first \(N\) terms is accurate to within an error that is less than the \((N+1)\)st term. The absolute value of the fourth term \(1/75{,}600\) is smaller than \(10^{-4}\) so we obtain the desired accuracy using the first three terms of the series for \(J\): \[ J \approx \frac13-\frac1{42} +\frac1{1320} \approx 0.31028 \] The error satisfies \[ \left|J- \left( \frac13-\frac1{42} +\frac1{1320}\right)\right|< \frac1{75{,}600} \approx1.3\times 10^{-5} \] The percentage error is less than 0.005% with just three terms.
Binomial Series
Isaac Newton discovered an important generalization of the Binomial Theorem around 1665. For any number \(a\) (integer or not) and integer \(n \geq 0\), we define the binomial coefficient: \[ \binom an = \frac{a(a-1)(a-2)\cdots (a- n+1)}{n!},\qquad \binom a0 = 1 \] For example, \[ \binom{6}3 = \frac{6\cdot 5\cdot 4}{3\cdot 2\cdot 1} = 20, \qquad \binom{\frac43}3 = \frac{\frac43\cdot \frac13\cdot \big(-\frac23\big)}{3\cdot 2\cdot 1} = -\frac4{81} \] Let \[ f(x) = (1+x)^a \] The Binomial Theorem of algebra (see Appendix C) states that for any whole number \(a\), \[ (r+s)^a = r^a + \binom{a}1 r^{a-1}s+ \binom{a}2 r^{a-2}s^2+\cdots+ \binom{a}{a-1} rs^{a-1} + s^a \] Setting \(r=1\) and \(s=x\), we obtain the expansion of \(f(x)\): \[ (1+x)^a = 1+ \binom{a}1 x+ \binom{a}2 x^2+\cdots+ \binom{a}{a-1} x^{a-1} + x^a \]
597
We derive Newton's generalization by computing the Maclaurin series of \(f(x)\) without assuming that \(a\) is a whole number. Observe that the derivatives follow a pattern: \[ \begin{equation*} \begin{array}{l@{\,}l@{\,}l@{\,}l@{\,}l} f(x) &=& (1 + x)^a &\qquad f(0) &=& 1\\ f'(x) &=& a(1+x)^{a-1} &\qquad f'(0) &=& a\\ f''(x) &=& a(a-1)(1+x)^{a-2} &\qquad f''(0) &=& a(a-1)\\ f'''(x) &=& a(a-1)(a-2)(1+x)^{a-3} &\qquad f'''(0) &=& a(a-1)(a-2) \end{array} \end{equation*} \] In general, \(f^{(n)}(0) = a(a-1)(a-2)\cdots (a-n+1)\) and \[ \frac{f^{(n)}(0)}{n!} = \frac{a(a-1)(a-2)\cdots (a- n+1)}{n!} = \binom an \] Hence the Maclaurin series for \(f(x) = (1+x)^a\) is the binomial series \[ \sum_{n=0}^\infty \binom an x^n = 1 + ax + \frac{a(a-1)}{2!}x^2 + \frac{a(a-1)(a-2)}{3!}x^3 + \cdots + \binom an x^n + \cdots \] The Ratio Test shows that this series has radius of convergence \(R=1\) (Exercise 86) and an additional argument (developed in Exercise 87) shows that it converges to \((1+x)^a\) for \(\left|x\right|<1\) .
When \(a\) is a whole number, \({\binom an}\) is zero for \(n>a\), and in this case, the binomial series breaks off at degree \(n\). The binomial series is an infinite series when \(a\) is not a whole number.
THEOREM 3 The Binomial Series
For any exponent \(a\) and for \(\left|x\right|<1\), \[ \begin{equation*}\boxed{\bbox[#FAF8ED,5pt]{ (1+x)^a = 1 + \frac{a}{1!}x + \frac{a(a-1)}{2!}x^2 + \frac{a(a-1)(a-2)}{3!}x^3 + \cdots + \binom an x^n + \cdots}} \end{equation*} \]
EXAMPLE 9
Find the terms through degree four in the Maclaurin expansion of \[ f(x) = (1 + x)^{4/3} \]
Solution The binomial coefficients \(\binom an\) for \(a = \tfrac{4}{3}\) for \(0<n<4\) are \[ 1, \qquad \frac{\frac{4}{3}}{1!} = \frac43, \qquad \frac{\frac{4}{3}\big(\frac{1}{3}\big)}{2!} = \frac29,\qquad \frac{\frac{4}{3}\big(\frac{1}{3}\big)\big(-\frac{2}{3}\big)}{3!} = -\frac4{81}, \qquad \frac{\frac{4}{3}\big(\frac{1}{3}\big)\big(-\frac{2}{3}\big)\big(-\frac{5}{3}\big)}{4!} = \frac{5}{243} \] Therefore, \( (1 + x)^{4/3} \approx 1 + \tfrac{4}{3}x + \tfrac{2}{9}x^2 - \tfrac{4}{81}x^3 + \tfrac{5}{243}x^4 + \cdots.\)
EXAMPLE 10
Find the Maclaurin series for \[f(x) = \frac1{\sqrt{1-x^2}}\]
Solution First, let’s find the coefficients in the binomial series for \((1+x)^{-1/2}\): \[ 1, \qquad \frac{-\frac12}{1!}=-\frac12, \qquad \frac{-\frac12\big(-\frac32\big)}{1\cdot2} = \frac{1\cdot 3}{2\cdot 4},\qquad \frac{-\frac12\big(-\frac32\big)\big(-\frac52\big)}{1\cdot2\cdot3} = \frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6} \] The general pattern is \[ \binom{-\frac12}{n} = \frac{-\frac12 \big(-\frac32\big)\big(-\frac52\big)\cdots\big(-\frac{2n-1}{2}\big)}{1\cdot2\cdot3\cdots n}= (-1)^n \frac{1\cdot3\cdot5\cdots(2n-1)}{2\cdot4\cdot6\cdot2n} \]
598
Thus, the following binomial expansion is valid for \(\left|x\right|<1\): \[ \frac1{\sqrt{1+x}} = 1 + \sum_{n=1}^\infty (-1)^n\frac{1\cdot 3\cdot 5 \cdots (2n-1)}{2\cdot 4\cdot 6 \cdots (2n)} x^n = 1 - \frac12 x + \frac{1\cdot 3}{2\cdot 4}x^2 - \cdots \] If \(\left|x\right| < 1\), then \(\left|x\right|^2 < 1\), and we can substitute \(-x^2\) for \(x\) to obtain \[ \begin{equation*} \frac{1}{\sqrt{1-x^2}} = 1 + \sum_{n=1}^\infty \frac{1\cdot 3\cdot 5 \cdots (2n-1)}{2\cdot 4\cdot 6 \cdots 2n} x^{2n} = 1 + \frac12x^2+\frac{1\cdot 3 }{2\cdot 4}x^4+\cdots\tag{4} \end{equation*} \]
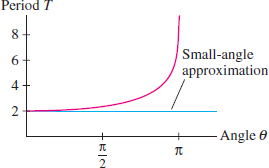
Taylor series are particularly useful for studying the so-called special functions (such as Bessel and hypergeometric functions) that appear in a wide range of physics and engineering applications. One example is the following elliptic function of the first kind, defined for \(\left|k\right| < 1\): \[ E(k) = \int_0^{\pi/2}\frac{dt}{\sqrt{1-k^2\sin^2t}} \] This function is used in physics to compute the period \(T\) of pendulum of length \(L\) released from an angle \(\theta\) (Figure 10.29). We can use the “small-angle approximation” \(T \approx 2\pi\sqrt{L/g}\) when \(\theta\) is small, but this approximation breaks down for large angles (Figure 10.30). The exact value of the period is \(T=4\sqrt{L/g}E(k)\), where \(k = \sin \frac12\theta\).
EXAMPLE 11 Elliptic Function
Find the Maclaurin series for \(E(k)\) and estimate \(E(k)\) for \(k=\sin\tfrac{\pi}{6}\).
Solution Substitute \(x = k\sin t\) in the Taylor expansion (4): \[ \frac1{\sqrt{1-k^2\sin^2t}} = 1 + \frac12k^2~\sin^2t+\frac{1\cdot 3}{2\cdot 4}k^4~\sin^4t+ \frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}k^6~\sin^6t+ \cdots \] This expansion is valid because \(\left|k\right|<1\) and hence \(\left|x\right| = \left|k\sin t\right| < 1\). Thus \(E(k)\) is equal to \[ \int_0^{\pi/2}\frac{dt}{\sqrt{1-k^2\sin^2~t}} = \int_0^{\pi/2} dt + \sum_{n=1}^\infty \frac{1\cdot 3 \cdots (2n-1)}{2\cdot 4 \cdot (2n)}\left(\int_0^{\pi/2}\sin^{2n}~t\,dt\right)k^{2n} \] According to Exercise 78 in Section 7.2, \[ \int_0^{\pi/2}\sin^{2n}~t\,dt = \left(\frac{1\cdot 3 \cdots (2n-1)}{2\cdot 4 \cdot (2n)}\right)\frac{\pi}2 \] This yields \[ E(k) = \frac{\pi}{2} + \frac{\pi}2\sum_{n=1}^\infty \left(\frac{1\cdot 3 \cdots (2n-1)^2}{2\cdot 4 \cdots (2n)}\right)^2k^{2n} \]
599
We approximate \(E(k)\) for \(k =\sin\big(\frac{\pi}6\big)=\frac12\) using the first five terms: \begin{align*} E\left(\frac12\right) &\approx \frac{\pi}2\left(1+\left(\frac12\right)^2\left(\frac12\right)^2+\left(\frac{1\cdot 3}{2\cdot 4}\right)^2\left(\frac12\right)^4\right.\\ &\qquad\quad\left. +\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)^2\left(\frac12\right)^6 +\left(\frac{1\cdot 3\cdot 5\cdot 7}{2\cdot 4\cdot 6\cdot 8}\right)^2\left(\frac12\right)^8 \right)\\ &\approx1.68517 \end{align*} The value given by a computer algebra system to seven places is \(E\big(\frac12\big) \approx 1.6856325\).
| Function \(f(x)\) | Maclaurin series | Converges to \(f(x)\) for |
| \(e^x\) | \(\displaystyle\sum_{n=0}^{\infty} \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots\) | All \(x\) |
| \(\sin x\) | \(\displaystyle\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n+1}}{(2n+1)!} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\) | All \(x\) |
| \(\cos x\) | \(\displaystyle\sum_{n=0}^{\infty} \frac{(-1)^{n}x^{2n}}{(2n)!} = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots\) | All \(x\) |
| \(\displaystyle\frac{1}{1-x}\) | \(\displaystyle\sum_{n=0}^{\infty} x^n = 1 + x + x^2 + x^3 + x^4 + \cdots\) | \(\left|x\right| < 1\) |
| \(\displaystyle\frac{1}{1+x}\) | \(\displaystyle\sum_{n=0}^{\infty} (-1)^nx^n = 1 - x + x^2 - x^3 + x^4 - \cdots\) | \(\left|x\right| < 1\) |
| \(\ln(1+x)\) | \(\displaystyle\sum_{n=1}^{\infty} \frac{(-1)^{n-1}x^n}{n} = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots\) | \(\left|x\right| < 1\) and \(x = 1\) |
| \(\tan^{-1}x\) | \(\displaystyle\sum_{n=0}^{\infty} \frac{(-1)^{n}x^{2n+1}}{2n+1} = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots\) | \(\left|x\right| < 1\) and \(x = 1\) |
| \((1+x)^a\) | \(\displaystyle\sum_{n=0}^{\infty} \binom an x^n = 1 + ax + \frac{a(a-1)}{2!}x^2 + \frac{a(a-1)(a-2)}{3!}x^3 + \cdots\) | \(\left|x\right| < 1\) |
10.7.1 Summary
- Taylor series of \(f(x)\) centered at \(x = c\): \[ T(x) = \sum_{n=0}^\infty\, \frac{f^{(n)}(c)}{n!}(x-c)^n \]
The partial sum \(T_k(x)\) is the \(k\)th Taylor polynomial.
- Maclaurin
series (\(c=0\)): \[
T(x) = \sum_{n=0}^\infty\, \frac{f^{(n)}(0)}{n!}x^n\]
600
- If \(f(x)\) is represented by a power series \({\displaystyle \sum_{n=0}^\infty a_n(x-c)^n}\) for \(|x-c|<R\) with \(R>0\), then this power series is necessarily the Taylor series centered at \(x=c\).
- A function \(f(x)\) is represented by its Taylor series \(T(x)\) if and only if the remainder \(R_k(x)=f(x)-T_k(x)\) tends to zero as \(k\to\infty\).
- Let \(I=(c-R, c+R)\) with \(R>0\). Suppose that there exists \(K>0\) such that \(|f^{(k)}(x)|<K\) for all \(x\in I\) and all \(k\). Then \(f(x)\) is represented by its Taylor series on \(I\); that is, \(f(x)= T(x)=\) for \(x\in I\).
- A good way to find the Taylor series of a function is to start with known Taylor series and apply one of the operations: differentiation, integration, multiplication, or substitution.
- For any exponent \(a\), the binomial expansion is valid for \(\left|x\right|<1\): \[ (1+x)^a = 1 + ax + \frac{a(a-1)}{2!}x^2 + \frac{a(a-1)(a-2)}{3!}x^3 + \cdots + \binom an x^n + \cdots \]