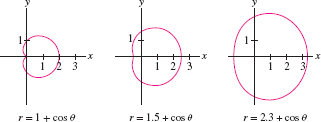Question 11.145

Points \(P\) and \(Q\) with the same radial coordinate (choose the correct answer):

1. (a) Lie on the same circle with the center at the origin.
2. (b) Lie on the same ray based at the origin.

Question 11.146

Give two polar representations for the point \((x,y) = (0,1)\), one with negative \(r\) and one with positive \(r\).

Question 11.147

Describe each of the following curves:

1. (a) \(r = 2\)
2. (b) \(r^2 = 2\)
3. (c) \(r\cos\theta = 2\)

Question 11.148

If \(f(-\theta) = f(\theta)\), then the curve \(r=f(\theta)\) is symmetric with respect to the (choose the correct answer):

1. (a) \(x\)-axis
2. (b) \(y\)-axis
3. (c) origin

Question 11.149

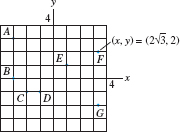
Find polar coordinates for each of the seven points plotted in Figure 11.53.

Question 11.150

Plot the points with polar coordinates:

1. (a) \(\big(2, \frac{\pi}{6}\big)\)
2. (b) \(\big(4, \frac{3\pi}{4}\big)\)
3. (c) \(\big(3, -\frac{\pi}{2}\big)\)
4. (d) \(\big(0, \frac{\pi}{6}\big)\)

Question 11.151

Convert from rectangular to polar coordinates.

1. (a) \((1, 0)\)
2. (b) \((3, \sqrt{3})\)
3. (c) \((-2, 2)\)
4. (d) \((-1, \sqrt 3)\)

Question 11.152

Convert from rectangular to polar coordinates using a calculator (make sure your choice of \(\theta\) gives the correct quadrant).

1. (a) \((2, 3)\)
2. (b) \((4, -7)\)
3. (c) \((-3, -8)\)
4. (d) \((-5, 2)\)

Question 11.153

Convert from polar to rectangular coordinates:

1. (a) \(\big(3, \frac{\pi}{6}\big)\)
2. (b) \(\big(6, \frac{3\pi}{4}\big)\)
3. (c) \(\big(0, \frac{\pi}{5}\big)\)
4. (d) \(\big(5, -\frac{\pi}{2}\big)\)

Question 11.154

Which of the following are possible polar coordinates for the point \(P\) with rectangular coordinates \((0, -2)\)?

1. (a) \(\left(2, \dfrac{\pi}{2}\right)\)
2. (b) \(\left(2, \dfrac{7\pi}{2}\right)\)
3. (c) \(\left(-2, -\dfrac{3\pi}{2}\right)\)
4. (d) \(\left(-2, \dfrac{7\pi}{2}\right)\)
5. (e) \(\left(-2, -\dfrac{\pi}{2}\right)\)
6. (f) \(\left(2, -\dfrac{7\pi}{2}\right)\)

Question 11.155

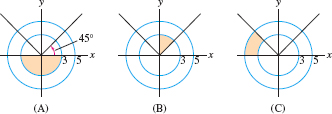
Describe each shaded sector in Figure 11.54 by inequalities in \(r\) and \(\theta\).

Question 11.156

Find the equation in polar coordinates of the line through the origin with slope \(\frac12\).

Question 11.157

What is the slope of the line \(\theta = \frac{3\pi}{5}\)?

Question 11.158

Which of \(r = 2\sec\theta\) and \(r=2\csc\theta\) defines a horizontal line?

Question 11.159

\(r = 7\)

Question 11.160

\(r = \sin\theta\)

Question 11.161

\(r = 2\sin\theta\)

Question 11.162

\(r = 2\csc\theta\)

Question 11.163

\(r = \dfrac{1}{\cos\theta - \sin\theta}\)

Question 11.164

\({r = \frac1{2-\cos\theta}}\)

Question 11.165

\(x^2 + y^2 = 5\)

Question 11.166

\(x = 5\)

Question 11.167

\(y = x^2\)

Question 11.168

\(xy = 1\)

Question 11.169

Match each equation with its description.

1. (a) \(r = 2\)
2. (b) \(\theta = 2\)
3. (c) \(r = 2\sec\theta\)
4. (d) \(r = 2\csc\theta\)
5. (i) Vertical line
6. (ii) Horizontal line
7. (iii) Circle
8. (iv) Line through origin

Question 11.170

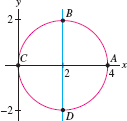
Find the values of \(\theta\) in the plot of \(r = 4\cos\theta\) corresponding to points \(A\), \(B\), \(C\), \(D\) in Figure 11.55. Then indicate the portion of the graph traced out as \(\theta\) varies in the following intervals:

1. (a) \(0\le\theta\le\frac{\pi}{2}\)
2. (b) \(\frac{\pi}{2}\le\theta\le\pi\)
3. (c) \(\pi\le\theta\le\frac{3\pi}2\)

Figure 11.55: Plot of \(r = 4\cos\theta\).

Question 11.171

Suppose that \(P = (x, y)\) has polar coordinates \((r, \theta)\). Find the polar coordinates for the points:

1. (a) \((x, -y)\)
2. (b) \((-x, -y)\)
3. (c) \((-x, y)\)
4. (d) \((y, x)\)

Question 11.172

Match each equation in rectangular coordinates with its equation in polar coordinates.

1. (a) \(x^2 + y^2 = 4\)
2. (b) \(x^2 + (y - 1)^2 = 1\)
3. (c) \(x^2 - y^2 = 4\)
4. (d) \(x + y = 4\)
5. (i) \(r^2(1 - 2\sin^2\theta) = 4\)
6. (ii) \(r(\cos\theta + \sin\theta) = 4\)
7. (iii) \(r = 2\sin\theta\)
8. (iv) \(r = 2\)

Question 11.173

What are the polar equations of the lines parallel to the line \(r\cos\big(\theta - \frac{\pi}3\big) = 1\)?

Question 11.174

Show that the circle with center at \(\big(\frac12, \frac12\big)\) in Figure 11.56 has polar equation \(r = \sin\theta+\cos\theta\) and find the values of \(\theta\) between \(0\) and \(\pi\) corresponding to points \(A, B\), \(C\), and \(D\).

Figure 11.56: Plot of \(r = \sin\theta + \cos\theta\).

Question 11.175

Sketch the curve \(r = \frac12\theta\) (the spiral of Archimedes) for \(\theta\) between \(0\) and \(2\pi\) by plotting the points for \(\theta = 0, \frac{\pi}4, \frac{\pi}2, \dots, 2\pi\).

Question 11.176

Sketch \(r = 3\cos\theta -1\) (see Example 8).

Question 11.177

Sketch the cardioid curve \(r = 1 + \cos\theta\).

Question 11.178

Show that the cardioid of Exercise 29 has equation \[(x^2 + y^2 - x)^2 = x^2 + y^2\]

in rectangular coordinates.

Question 11.179

Figure 11.57 displays the graphs of \(r = \sin 2\theta\) in rectangular coordinates and in polar coordinates, where it is a “rose with four petals.” Identify:

1. (a) The points in (B) corresponding to points \(A\)-\(I\) in (A).
2. (b) The parts of the curve in (B) corresponding to the angle intervals \(\bigl[0, \frac{\pi}{2}\bigr]\), \(\bigl[\frac{\pi}{2}, \pi\bigr]\), \(\bigl[\pi, \frac{3\pi}{2}\bigr]\), and \(\bigl[\frac{3\pi}{2}, 2\pi\bigr]\).

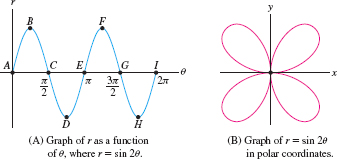
633

Question 11.180

Sketch the curve \(r = \sin 3\theta\). First fill in the table of \(r\)-values below and plot the corresponding points of the curve. Notice that the three petals of the curve correspond to the angle intervals \(\bigl[0,\frac{\pi}{3}\bigr]\), \(\bigl[\frac{\pi}{3}, \frac{2\pi}{3}\bigr]\), and \(\bigl[\frac{\pi}{3}, \pi\bigr]\). Then plot \(r = \sin 3\theta\) in rectangular coordinates and label the points on this graph corresponding to \((r, \theta)\) in the table.

Question 11.181

Plot the cissoid \(r = 2\sin\theta\tan\theta\) and show that its equation in rectangular coordinates is \[{y^2 = \frac{x^3}{2 - x}}\]

Question 11.182

Prove that \(r = 2a\cos\theta\) is the equation of the circle in Figure 11.58 using only the fact that a triangle inscribed in a circle with one side a diameter is a right triangle.

Question 11.183

Show that \[r = a\cos\theta + b\sin\theta\]

is the equation of a circle passing through the origin. Express the radius and center (in rectangular coordinates) in terms of \(a\) and \(b\).

Question 11.184

Use the previous exercise to write the equation of the circle of radius \(5\) and center \((3,4)\) in the form \(r = a\cos\theta + b\sin\theta\).

Question 11.185

Use the identity \(\cos2\theta = \cos^2\theta - \sin^2\theta\) to find a polar equation of the hyperbola \(x^2 - y^2 = 1\).

Question 11.186

Find an equation in rectangular coordinates for the curve \(r^2 = \cos2\theta\).

Question 11.187

Show that \(\cos 3\theta = \cos^3\theta - 3\cos\theta\sin^2\theta\) and use this identity to find an equation in rectangular coordinates for the curve \(r = \cos 3\theta\).

Question 11.188

Use the addition formula for the cosine to show that the line \(\mathcal L\) with polar equation \({r\cos(\theta - \alpha) = d}\) has the equation in rectangular coordinates \((\cos\alpha)x + (\sin\alpha)y = d\). Show that \(\mathcal L\) has slope \(m = - \cot\alpha\) and \(y\)-intercept \({d}/{\sin\alpha}\).

Question 11.189

The point on \(\mathcal L\) closest to the origin has polar coordinates \(\bigl(2, \frac{\pi}9\bigr)\).

Question 11.190

The point on \(\mathcal L\) closest to the origin has rectangular coordinates \((-2, 2)\).

Question 11.191

\(\mathcal L\) is tangent to the circle \(r = 2\sqrt{10}\) at the point with rectangular coordinates \((-2, -6)\).

Question 11.192

\(\mathcal L\) has slope \(3\) and is tangent to the unit circle in the fourth quadrant.

Question 11.193

Show that every line that does not pass through the origin has a polar equation of the form \(r = \frac{b}{\sin\theta - a\cos\theta}\)

where \(b\ ≠ 0\).

Question 11.194

By the Law of Cosines, the distance \(d\) between two points (Figure 11.59) with polar coordinates \((r, \theta)\) and \((r_0, \theta_0)\) is \begin{equation*} d^2 = r^2 + r_0^2 -2rr_0\cos(\theta-\theta_0) \end{equation*}

Use this distance formula to show that \[ r^2 - 10r\cos\left(\theta - \frac{\pi}4\right) = 56 \]

is the equation of the circle of radius 9 whose center has polar coordinates \(\bigl(5,\frac{\pi}4\bigr)\).

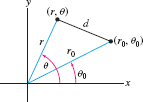
Question 11.195

For \(a > 0\), a lemniscate curve is the set of points \(P\) such that the product of the distances from \(P\) to \((a,0)\) and \((-a, 0)\) is \(a^2\). Show that the equation of the lemniscate is \[ (x^2 + y^2)^2 = 2a^2(x^2 - y^2) \]

Then find the equation in polar coordinates. To obtain the simplest form of the equation, use the identity \(\cos 2\theta = \cos^2\theta - \sin^2 \theta\). Plot the lemniscate for \(a = 2\) if you have a computer algebra system.

Question 11.196

Let \(c\) be a fixed constant. Explain the relationship between the graphs of:

1. (a) \(y = f(x+c)\) and \(y = f(x)\) (rectangular)
2. (b) \(r = f(\theta+c)\) and \(r = f(\theta)\) (polar)
3. (c) \(y = f(x)+c\) and \(y = f(x)\) (rectangular)
4. (d) \(r = f(\theta)+c\) and \(r = f(\theta)\) (polar)

Question 11.197

The Derivative in Polar Coordinates Show that a polar curve \(r = f(\theta)\) has parametric equations \[ x= f(\theta)\cos\theta, \qquad y= f(\theta)\sin\theta \]

Then apply Theorem 2 of Section 11.1 to prove \begin{equation} \label{12.expolar.derivative} \frac{dy}{dx} = \frac{f(\theta)\cos\theta + f'(\theta)\sin\theta}{-f(\theta)\sin\theta + f'(\theta)\cos\theta}\tag{2} \end{equation}

where \(f'(\theta) = df/d\theta\).

Question 11.198

Use Eq. (2) to find the slope of the tangent line to \(r = \sin\theta\) at \(\theta = \frac{\pi}3\).

Question 11.199

Use Eq. (2) to find the slope of the tangent line to \(r = \theta\) at \(\theta=\frac{\pi}2\) and \(\theta = \pi\).

Question 11.200

Find the equation in rectangular coordinates of the tangent line to \(r = 4\cos 3\theta\) at \(\theta = \frac{\pi}6\).

Question 11.201

Find the polar coordinates of the points on the lemniscate \(r^2 = \cos 2t\) in Figure 11.60 where the tangent line is horizontal.

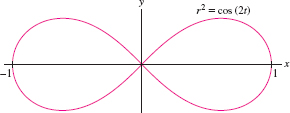
Question 11.202

Find the polar coordinates of the points on the cardioid \(r = 1 + \cos\theta\) where the tangent line is horizontal (see Figure 11.61).

Question 11.203

Use Eq. (2) to show that for \(r = \sin\theta + \cos\theta\), \( \frac{dy}{dx} = \frac{\cos2\theta + \sin 2\theta}{\cos 2\theta - \sin 2\theta} \)

Then calculate the slopes of the tangent lines at points \(A, B, C\) in Figure 11.56.

Question 11.204

Let \(f(x)\) be a periodic function of period \(2\pi\)—that is, \(f(x) = f(x + 2\pi)\). Explain how this periodicity is reflected in the graph of:

1. (a) \(y = f(x)\) in rectangular coordinates
2. (b) \(r = f(\theta)\) in polar coordinates

Question 11.205

Use a graphing utility to convince yourself that the polar equations \(r = f_1(\theta) = 2\cos\theta -1\) and \(r = f_2(\theta) = 2\cos\theta + 1\) have the same graph. Then explain why. Hint: Show that the points \((f_1(\theta + \pi),\theta + \pi)\) and \((f_2(\theta),\theta)\) coincide.

Question 11.206

We investigate how the shape of the limaçon curve \(r = b + \cos\theta\) depends on the constant \(b\) (see Figure 11.61).

1. (a) Argue as in Exercise 57 to show that the constants \(b\) and \(-b\) yield the same curve.
2. (b) Plot the limaçon for \(b = 0, 0.2, 0.5, 0.8, 1\) and describe how the curve changes.
3. (c) Plot the limaçon for \(1.2, 1.5, 1.8, 2, 2.4\) and describe how the curve changes.
4. (d) Use Eq. (2) to show that \[ { \frac{dy}{dx} = -\left(\frac{b\cos \theta + \cos 2\theta}{b + 2\cos \theta}\right)\csc \theta}\]
5. (e) Find the points where the tangent line is vertical. Note that there are three cases: \(0 \le b \lt 2\), \(b = 1\), and \(b \gt 2\). Do the plots constructed in (b) and (c) reflect your results?