11.10 Area and Arc Length in Polar Coordinates
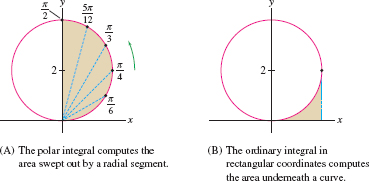
Integration in polar coordinates involves finding not the area underneath a curve but, rather, the area of a sector bounded by a curve as in Figure 11.62. Consider the region bounded by the curve \(r = f(\theta)\) and the two rays \(\theta = \alpha\) and \(\theta = \beta\) with \(\alpha \lt \beta\). To derive a formula for the area, divide the region into \(N\) narrow sectors of angle \(\Delta\theta = ({\beta - \alpha})/N\) corresponding to a partition of the interval \([\alpha,\beta]\): \[ \theta_0 = \alpha \lt \theta_1 \lt \theta_2 \lt \cdots \lt \theta_N = \beta \]
635
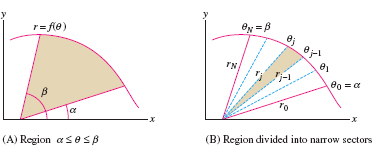
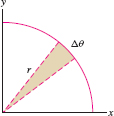
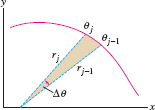
Recall that a circular sector of angle \(\Delta \theta\) and radius \(r\) has area \(\frac12r^2\Delta\theta\) (Figure 11.63). If \(\Delta\theta\) is small, the \(j\)th narrow sector (Figure 11.64) is nearly a circular sector of radius \(r_j = f(\theta_j)\), so its area is approximately \(\frac12r_j^2\Delta\theta\). The total area is approximated by the sum: \begin{equation} \label{12.polarea.rsum} \textrm{Area of region}\approx\sum_{j = 1}^N \frac12r_j^2 \Delta\theta = \frac12\sum_{j = 1}^N f(\theta_j)^2 \Delta\theta\tag{1} \end{equation}
This is a Riemann sum for the integral \({\displaystyle\frac12\int_{\alpha}^{\beta} f(\theta)^2\, d\theta}\). If \(f(\theta)\) is continuous, then the sum approaches the integral as \(N\to\infty\), and we obtain the following formula.
THEOREM 1
Area in Polar Coordinates If \(f(\theta)\) is a continuous function, then the area bounded by a curve in polar form \(r = f(\theta)\) and the rays \(\theta = \alpha\) and \(\theta = \beta\) (with \(\alpha \lt \beta\)) is equal to \begin{equation} \label{12.polarea.formula}\boxed{\bbox[#fef7e5,5pt]{ \frac12 \int_{\alpha}^{\beta} r^2 \, d\theta = \frac12 \int_{\alpha}^{\beta} f(\theta)^2 \, d\theta}}\tag{2} \end{equation}
We know that \(r = R\) defines a circle of radius \(R\). By Eq. (2), the area is equal to \(\displaystyle\frac12\int_0^{2\pi}R^2\,d\theta = \frac12R^2(2\pi)=\pi R^2\), as expected.
EXAMPLE 1
Use Theorem 1 to compute the area of the right semicircle with equation \(r = 4\sin\theta\).
REMINDER
In Eq. (4), we use the identity \begin{equation} \label{12.polarea.trigid} \sin^2\theta = \frac12(1 - \cos 2\theta)\tag{3} \end{equation}
Solution The equation \(r = 4\sin\theta\) defines a circle of radius 2 tangent to the \(x\)-axis at the origin. The right semicircle is “swept out” as \(\theta\) varies from 0 to \(\frac{\pi}2\) as in Figure 11.65. By Eq. (2), the area of the right semicircle is \begin{align} \frac12\int_0^{\pi/2} r^2\,d\theta & = \frac12 \int_0^{\pi/2} (4\sin\theta)^2 \, d\theta = 8\int_0^{\pi/2} \sin^2\theta\,d\theta\tag{4}\\ &=8\int_0^{\pi/2} \frac12 (1-\cos2\theta)\, d\theta\notag\\ &= (4\theta - 2\sin 2\theta)\bigg\vert_0^{\pi/2} = 4\left(\frac{\pi}{2}\right) - 0 = 2\pi \notag \end{align}
636
CAUTION
Keep in mind that the integral \({\frac12\int_\alpha^\beta r^2\,d\theta}\) does not compute the area under a curve as in Figure 11.65, but rather computes the area “swept out” by a radial segment as \(\theta\) varies from \(\alpha\) to \(\beta\), as in Figure 11.65.
EXAMPLE 2
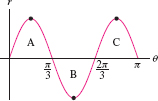
Sketch \(r = \sin 3\theta\) and compute the area of one “petal.”
Solution To sketch the curve, we first graph \(r = \sin 3\theta\) in rectangular coordinates. Figure 11.66 shows that the radius \(r\) varies from \(0\) to \(1\) and back to \(0\) as \(\theta\) varies from \(0\) to \(\frac{\pi}{3}\). This gives petal A in Figure 11.67. Petal B is traced as \(\theta\) varies from \(\frac{\pi}{3}\) to \(\frac{2\pi}{3}\) (with \(r \leq 0\)), and petal C is traced for \(\frac{2\pi}{3} \le \theta\le \pi\). We find that the area of petal \(A\) (using Eq. (3) in the margin of the previous page to evaluate the integral) is equal to \[ \frac12\int_0^{\pi/3} (\sin 3\theta)^2\,d\theta = \frac12\int_0^{\pi/3} \left(\frac{1-\cos 6\theta}2 \right) \,d\theta = \left(\frac14 \theta - \frac1{24}\sin 6\theta \right)\bigg|_0^{\pi/3} = \frac{\pi}{12} \]

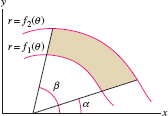
The area between two polar curves \(r = f_1(\theta)\) and \(r = f_2(\theta)\) with \(f_2(\theta)\ge f_1(\theta)\), for \(\alpha\le \theta\le \beta\), is equal to (Figure 11.68): \begin{equation} \boxed{\bbox[#fef7e5,5pt]{ \textrm{Area between two curves} = \frac12\int_\alpha^\beta \big(f_2(\theta)^2 - f_1(\theta)^2\big)\,d\theta}}\tag{5} \end{equation}
EXAMPLE 3 Area Between Two Curves
Find the area of the region inside the circle \(r = 2\cos \theta\) but outside the circle \(r = 1\) [Figure 11.69].
Solution The two circles intersect at the points where \((r, 2\cos\theta)= (r, 1)\) or in other words, when \(2\cos\theta = 1\). This yields \(\cos\theta = \frac12\), which has solutions \(\theta = \pm\frac{\pi}3\).
637

We see in Figure 11.69 that region (I) is the difference of regions (II) and (III) in Figure 11.69 and Figure 11.69. Therefore, \begin{align} \textrm{Area of (I)} &= \textrm{area of (II)} - \textrm{area of (III)}\notag\\ &=\frac12\int_{-\pi/3}^{\pi/3} (2\cos \theta)^2\, d\theta - \frac12\int_{-\pi/3}^{\pi/3} (1)^2\, d\theta\notag\\ &=\frac12 \int_{-\pi/3}^{\pi/3} (4\cos^2 \theta-1)\, d\theta =\frac12 \int_{-\pi/3}^{\pi/3} (2\cos2\theta+1)\,d\theta\tag{6} \\ &= \frac12(\sin2\theta + \theta)\bigg|_{-\pi/3}^{\pi/3} = \frac{\sqrt{3}}2+\frac{\pi}3\notag \end{align}
REMINDER
In Eq. (6), we use the identity \[ \cos^2\theta=\frac12(1+\cos2\theta) \]
We close this section by deriving a formula for arc length in polar coordinates. Observe that a polar curve \(r = f(\theta)\) has a parametrization with \(\theta\) as a parameter: \[ x = r\cos\theta = f(\theta)\cos\theta,\qquad y = r\sin\theta = f(\theta)\sin\theta \]
Using a prime to denote the derivative with respect to \(\theta\), we have \begin{align*} x'(\theta)= \frac{dx}{d\theta} =-f(\theta)\sin\theta + f'(\theta)\cos\theta\\ y'(\theta) = \frac{dy}{d\theta} = f(\theta)\cos\theta+f'(\theta)\sin\theta \end{align*}
Recall from Section 11.2 that arc length is obtained by integrating \({\sqrt{x'(\theta)^2 + y'(\theta)^2}}\). Straightforward algebra shows that \({x'(\theta)^2 + y'(\theta)^2 = f(\theta)^2 + f'(\theta)^2}\), and thus \begin{equation} \label{12.polar.polararc} \boxed{\bbox[#fef7e5,5pt]{\textrm{Arc length \(s\)} = \int_{\alpha}^{\beta} \sqrt{ f(\theta)^2 + f'(\theta)^2} \, d\theta }}\tag{7} \end{equation}
EXAMPLE 4
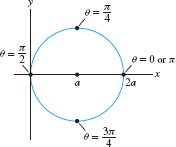
Find the total length of the circle \(r = 2a\cos\theta\) for \(a > 0\).
Solution In this case, \(f(\theta) = 2a\cos\theta\) and \[ f(\theta)^2 + f'(\theta)^2 = 4a^2\cos^2 \theta + 4a^2\sin^2 \theta = 4a^2 \]
The total length of this circle of radius \(a\) has the expected value: \[ \int_0^{\pi} \sqrt{f(\theta)^2 + f'(\theta)^2} \, d\theta = \int_0^{\pi} (2a)\, d\theta = 2\pi a \]
Note that the upper limit of integration is \(\pi\) rather than \(2\pi\) because the entire circle is traced out as \(\theta\) varies from \(0\) to \(\pi\) (see Figure 11.70).