11.11 SUMMARY

• Area of the sector bounded by a polar curve \(r = f(\theta)\) and two rays \(\theta = \alpha\) and \(\theta = \beta\) (Figure 11.71): \[ \mathrm{Area} = \frac12\int_{\alpha}^{\beta} f(\theta)^2\, d\theta \]
• Area between \(r=f_1(\theta)\) and \(r=f_2(\theta)\), where \(f_2(\theta)\ge f_1(\theta)\) (Figure 11.72): \[ \mathrm{Area} = \frac12\int_{\alpha}^{\beta} \bigl(f_2(\theta)^2 - f_1(\theta)^2\bigr)\, d\theta \]
  

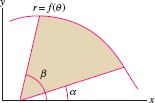  Figure 11.71: Region bounded by the polar curve \(r=f(\theta)\) and the rays \(\theta=\alpha\), \(\theta=\beta\).
  

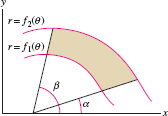  Figure 11.72: Region between two polar curves.
• Arc length of the polar curve \(r = f(\theta)\) for \(\alpha\le \theta \le \beta\): \[ \textrm{Arc length} = \int_{\alpha}^{\beta} \sqrt{f(\theta)^2 + f'(\theta)^2}\, d\theta \]