Question 11.207

Polar coordinates are suited to finding the area (choose one):

• (a) Under a curve between \(x = a\) and \(x = b\).
• (b) Bounded by a curve and two rays through the origin.

Question 11.208

Is the formula for area in polar coordinates valid if \(f(\theta)\) takes negative values?

Question 11.209

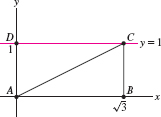
The horizontal line \(y=1\) has polar equation \(r=\csc\theta\). Which area is represented by the integral \(\frac12\int_{\pi/6}^{\pi/2} \csc^2\theta\ d\theta\) (Figure 11.73)?

• (a) \(\square ABCD\)
• (b) \(\triangle ABC\)
• (c) \(\triangle ACD\)

Question 11.210

Sketch the area bounded by the circle \(r = 5\) and the rays \(\theta = \frac{\pi}{2}\) and \(\theta = \pi\), and compute its area as an integral in polar coordinates.

Question 11.211

Sketch the region bounded by the line \(r=\sec\theta\) and the rays \(\theta = 0\) and \(\theta = \frac{\pi}3\). Compute its area in two ways: as an integral in polar coordinates and using geometry.

Question 11.212

Calculate the area of the circle \(r = 4\sin\theta\) as an integral in polar coordinates (see Figure 11.65). Be careful to choose the correct limits of integration.

Question 11.213

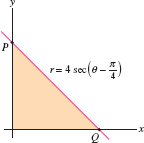
Find the area of the shaded triangle in Figure 11.74 as an integral in polar coordinates. Then find the rectangular coordinates of \(P\) and \(Q\) and compute the area via geometry.

Question 11.214

Find the area of the shaded region in Figure 11.75. Note that \(\theta\) varies from \(0\) to \(\frac{\pi}2\).

Question 11.215

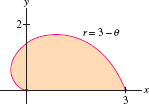
Which interval of \(\theta\)-values corresponds to the the shaded region in Figure 11.76? Find the area of the region.

Question 11.216

Find the total area enclosed by the cardioid in Figure 11.77.

Figure 11.77: The cardioid \(r=1-\cos\theta\).

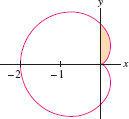
Question 11.217

Find the area of the shaded region in Figure 11.77.

Question 11.218

Find the area of one leaf of the “four-petaled rose” \(r = \sin 2\theta\) (Figure 11.78). Then prove that the total area of the rose is equal to one-half the area of the circumscribed circle.

Figure 11.78: Four-petaled rose \(r = \sin 2\theta\).

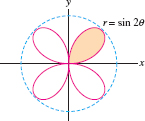
Question 11.219

Find the area enclosed by one loop of the lemniscate with equation \(r^2=\cos 2\theta\) (Figure 11.79). Choose your limits of integration carefully.

Figure 11.79: The lemniscate \(r^2=\cos 2\theta\).

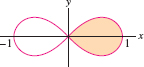
Question 11.220

Sketch the spiral \(r = \theta\) for \(0\le \theta\le 2\pi\) and find the area bounded by the curve and the first quadrant.

Question 11.221

Find the area of the intersection of the circles \(r=\sin\theta\) and \(r=\cos\theta\).

Question 11.222

Find the area of region \(A\) in Figure 11.80.

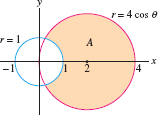
Question 11.223

Find the area of the shaded region in Figure 11.81, enclosed by the circle \(r=\frac12\) and a petal of the curve \(r=\cos3\theta\). Hint: Compute the area of both the petal and the region inside the petal and outside the circle.

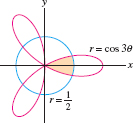
Question 11.224

Find the area of the inner loop of the limaçon with polar equation \(r = 2\cos\theta - 1\) (Figure 11.82).

640

Question 11.225

Find the area of the shaded region in Figure 11.82 between the inner and outer loop of the limaçon \(r = 2\cos\theta-1\).

Figure 11.82: The limaçon \(r = 2\cos\theta-1\).

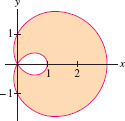
Question 11.226

Find the area of the part of the circle \(r = \sin\theta+\cos\theta\) in the fourth quadrant (see Exercise 26 in Section 11.3).

Question 11.227

Find the area of the region inside the circle \(r = 2\sin\big(\theta+\frac{\pi}4\big)\) and above the line \(r = \sec\big(\theta-\frac{\pi}4\big)\).

Question 11.228

Find the area between the two curves in Figure 11.83.

Question 11.229

Find the area between the two curves in Figure 11.83.

Question 11.230

Find the area inside both curves in Figure 11.84.

Question 11.231

Find the area of the region that lies inside one but not both of the curves in Figure 11.84.

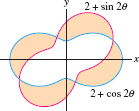
Question 11.232

Calculate the total length of the circle \(r = 4\sin\theta \) as an integral in polar coordinates.

Question 11.233

Sketch the segment \(r = \sec\theta\) for \(0\le \theta\le A\). Then compute its length in two ways: as an integral in polar coordinates and using trigonometry.

Question 11.234

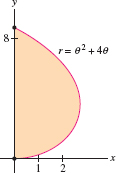
The length of \(r = \theta^2\) for \(0\le \theta\le \pi\)

Question 11.235

The spiral \(r = \theta\) for \(0\le \theta\le A\)

Question 11.236

The equiangular spiral \(r = e^\theta\) for \(0 \le \theta\le 2\pi\)

Question 11.237

The inner loop of \(r = 2\cos\theta-1\) in Figure 11.82

Question 11.238

The cardioid \(r = 1-\cos\theta\) in Figure 11.77

Question 11.239

\(r = \cos^2\theta\)

Question 11.240

\(r = (2-\cos\theta)^{-1}\),\(\quad\)\(0\le \theta\le 2\pi\)

Question 11.241

\(r = \sin^3t\),\(\quad\)\(0\le \theta\le 2\pi\)

Question 11.242

The three-petal rose \(r=\cos3\theta\) in Figure 11.81

Question 11.243

The curve \(r=2+\sin 2\theta\) in Figure 11.84

Question 11.244

The curve \(r=\theta \sin\theta\) in Figure 11.85 for \(0\le \theta\le 4\pi\)

Figure 11.85: \(r=\theta \sin\theta\) for \(0\le \theta\le 4\pi\).

Question 11.245

\(r= \sqrt{\theta}\),\(\quad\)\(0\le\theta\le 4\pi\)

Question 11.246

Suppose that the polar coordinates of a moving particle at time \(t\) are \((r(t),\theta(t))\). Prove that the particle's speed is equal to \(\sqrt{(dr/dt)^2 + r^2 (d\theta/dt)^2}\).

Question 11.247

Compute the speed at time \(t=1\) of a particle whose polar coordinates at time \(t\) are \(r= t\), \(\theta = t\) (use Exercise 37). What would the speed be if the particle's rectangular coordinates were \(x=t, y=t\)? Why is the speed increasing in one case and constant in the other?