Question 11.248

Which of the following equations defines an ellipse? Which does not define a conic section?

• (a) \(4x^2-9y^2= 12\)
• (b) \(-4x +9y^2= 0\)
• (c) \(4y^2+9x^2= 12\)
• (d) \(4x^3+9y^3= 12\)

Question 11.249

For which conic sections do the vertices lie between the foci?

Question 11.250

What are the foci of \[{\left(\frac{x}a\right)^2+\left(\frac{y}b\right)^2=1} \quad\text{if \(a \lt b\)?}\]

Question 11.251

What is the geometric interpretation of \({b}/{a}\) in the equation of a hyperbola in standard position?

Question 11.252

\({\left(\frac{x}9\right)^2 + \left(\frac{y}4\right)^2 = 1}\)

Question 11.253

\({ \frac{x^2}9 + \frac{y^2}4 = 1}\)

Question 11.254

\({\left(\frac{x}{4}\right)^2 - \left(\frac{y}{9}\right)^2 = 1}\)

Question 11.255

\({ \frac{x^2}{4} - \frac{y^2}{9} = 36}\)

Question 11.256

\({\left(\frac{x-3}7\right)^2 - \left(\frac{y+1}4\right)^2 = 1}\)

Question 11.257

\({\left(\frac{x-3}4\right)^2 + \left(\frac{y+1}7\right)^2 = 1}\)

Question 11.258

Translated with center at the origin

Question 11.259

Translated with center at \((-2,-12)\)

Question 11.260

Translated to the right six units

Question 11.261

Translated down four units

Question 11.262

Vertices \((\pm 5, 0)\) and \((0,\pm 7)\)

Question 11.263

Foci \((\pm 6,0)\) and focal vertices \((\pm 10,0)\)

Question 11.264

Foci \((0, \pm 10)\) and eccentricity \(e=\frac35\)

Question 11.265

Vertices \((4,0)\), \((28,0)\) and eccentricity \(e=\frac23\)

Question 11.266

Vertices \((\pm 3, 0)\) and foci \((\pm 5,0)\)

Question 11.267

Vertices \((\pm 3,0)\) and asymptotes \(y= \pm \frac12 x\)

Question 11.268

Foci \((\pm 4,0)\) and eccentricity \(e= 2\)

Question 11.269

Vertices \((0,\pm 6)\) and eccentricity \(e= 3\)

Question 11.270

Vertices \((-3,0)\), \((7,0)\) and eccentricity \(e=3\)

Question 11.271

Vertices \((0,-6)\), \((0,4)\) and foci \((0, -9)\), \((0,7)\)

Question 11.272

Vertex \((0,0)\), focus \(\big(\frac1{12},0\big)\)

Question 11.273

Vertex \((0,0)\), focus \((0,2)\)

Question 11.274

Vertex \((0,0)\), directrix \(y=-5\)

Question 11.275

Vertex \((3,4)\), directrix \(y=-2\)

Question 11.276

Focus \((0,4)\), directrix \(y=-4\)

Question 11.277

Focus \((0,-4)\), directrix \(y=4\)

Question 11.278

Focus \((2,0)\), directrix \(x=-2\)

Question 11.279

Focus \((-2,0)\), vertex \((2,0)\)

Question 11.280

\(x^2+4y^2 = 16\)

Question 11.281

\(4x^2+y^2 = 16\)

Question 11.282

\({\left(\frac{x-3}{4}\right)^2 -\left(\frac{y+5}{7}\right)^2 = 1}\)

Question 11.283

\(3x^2-27y^2 = 12\)

Question 11.284

\({4x^2-3y^2+8x+30y=215}\)

Question 11.285

\({y = 4x^2}\)

Question 11.286

\({y = 4(x-4)^2}\)

Question 11.287

\({8y^2+6x^2-36x-64y+134=0}\)

Question 11.288

\({4x^2+25y^2 -8x-10y= 20}\)

Question 11.289

\({16x^2+25y^2-64x-200y+64=0}\)

Question 11.290

\({4x^2+5xy + 7y^2 = 24}\)

Question 11.291

\({x^2 - 2x y + y^2 + 24x - 8 = 0}\)

Question 11.292

\({2x^2 - 8xy + 3y^2 - 4=0}\)

Question 11.293

\({2x^2 - 3xy + 5y^2 - 4=0}\)

Question 11.294

Show that the “conic” \({x^2+3y^2-6x+12+23=0}\) has no points.

Question 11.295

For which values of \(a\) does the conic \({3 x^2 +2 y^2 - 16y + 12 x =a}\) have at least one point?

Question 11.296

Show that \({\frac{b}a = \sqrt{1-e^2}}\) for a standard ellipse of eccentricity \(e\).

Question 11.297

Show that the eccentricity of a hyperbola in standard position is \(e = \sqrt{1+m^2}\), where \(\pm m\) are the slopes of the asymptotes.

Question 11.298

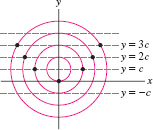
Explain why the dots in Figure 11.108 lie on a parabola. Where are the focus and directrix located?

Question 11.299

Find the equation of the ellipse consisting of points \(P\) such that \(PF_1+PF_2=12\), where \(F_1=(4,0)\) and \(F_2=(-2,0)\).

Question 11.300

A latus rectum of a conic section is a chord through a focus parallel to the directrix. Find the area bounded by the parabola \(y=x^2/(4c)\) and its latus rectum (refer to Figure 11.93).

Question 11.301

Show that the tangent line at a point \(P=(x_0,y_0)\) on the hyperbola \({\left(\frac{x}a\right)^2-\left(\frac{y}b\right)^2=1}\) has equation \[ Ax-By=1 \] where \({A=\frac{x_0}{a^2}}\) and \({B=\frac{y_0}{b^2}}\).

Question 11.302

\(e=\frac12\),\(\quad\) \(x=3\)

Question 11.303

\(e=\frac12\),\(\quad\) \(x=-3\)

Question 11.304

\(e=1\),\(\quad\) \(x=4\)

Question 11.305

\(e=\frac32\),\(\quad\) \(x=-4\)

Question 11.306

\({r = \frac{8}{1+4\cos\theta}}\)

Question 11.307

\({r = \frac{8}{4+\cos\theta}}\)

Question 11.308

\({r = \frac{8}{4+3\cos\theta}}\)

Question 11.309

\({r = \frac{12}{4+3\cos\theta}}\)

Question 11.310

Find a polar equation for the hyperbola with focus at the origin, directrix \(x=-2\), and eccentricity \(e=1.2\).

Question 11.311

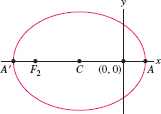
Let \(\mathcal C\) be the ellipse \({r={de}/({1+e\cos\theta})}\), where \(e \lt 1\). Show that the \(x\)-coordinates of the points in Figure 11.109 are as follows:

Question 11.312

Find an equation in rectangular coordinates of the conic \[ r = \frac{16}{5+3\cos\theta} \]

Hint: Use the results of Exercise 60.

Question 11.313

Let \(e \gt 1\). Show that the vertices of the hyperbola \({r=\frac{de}{1+e\cos\theta}}\) have \(x\)-coordinates \({\frac{ed}{e+1}}\) and \({\frac{ed}{e-1}}\).

Question 11.314

Kepler's First Law states that planetary orbits are ellipses with the sun at one focus. The orbit of Pluto has eccentricity \(e\approx 0.25\). Its perihelion (closest distance to the sun) is approximately 2.7 billion miles. Find the aphelion (farthest distance from the sun).

Question 11.315

Kepler's Third Law states that the ratio \(T/a^{3/2}\) is equal to a constant \(C\) for all planetary orbits around the sun, where \(T\) is the period (time for a complete orbit) and \(a\) is the semimajor axis.

• (a) Compute \(C\) in units of days and kilometers, given that the semimajor axis of the earth's orbit is \(150\times 10^6\) km.
• (b) Compute the period of Saturn's orbit, given that its semimajor axis is approximately \(1.43\times 10^9\) km.
• (c) Saturn's orbit has eccentricity \(e=0.056\). Find the perihelion and aphelion of Saturn (see Exercise 63).

Question 11.316

Verify Theorem 2.

Question 11.317

Verify Theorem 5 in the case \(0 \lt e \lt 1\). Hint: Repeat the proof of Theorem 5, but set \(c = d/(e^{-2}-1)\).

Question 11.318

Verify that if \(e \gt 1\), then Eq.(11) defines a hyperbola of eccentricity \(e\), with its focus at the origin and directrix at \(x=d\).

Question 11.319

Show that the equation of the tangent line at \(P\) is \(Ax+By=1\), where \({A=\frac{x_0}{a^2}}\) and \({B=\frac{y_0}{b^2}}\).

Question 11.320

Points \(R_1\) and \(R_2\) in Figure 11.110 are defined so that \(\overline{F_1R_1}\) and \(\overline{F_2R_2}\) are perpendicular to the tangent line.

Figure 11.110: The ellipse \({\left(\frac{x}a\right)^2 + \left(\frac{y}b\right)^2 = 1}\).

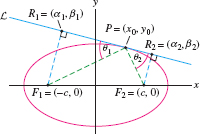
• (a) Show, with \(A\) and \(B\) as in Exercise 68, that \[ \frac{\alpha_1+c}{\beta_1} = \frac{\alpha_2-c}{\beta_2} = \frac{A}B \]
• (b) Use (a) and the distance formula to show that \[ \frac{{F_1R_1}}{{F_2R_2}} = \frac{\beta_1}{\beta_2} \]
• (c) Use (a) and the equation of the tangent line in Exercise 68 to show that \[ \beta_1=\frac{B(1+Ac)}{A^2+B^2},\qquad \beta_2=\frac{B(1-Ac)}{A^2+B^2} \]

Question 11.321

• (a) Prove that \({PF_1} = a+x_0e\) and \({PF_2} = a-x_0e\). Hint: Show that \({PF_1}^2-{PF_2}^2 = 4x_0c\). Then use the defining property \({PF_1}+{PF_2}=2a\) and the relation \(e=c/a\).
• (b) Verify that \({\frac{{F_1R_1}}{{PF_1}} = \frac{{F_2R_2}}{{PF_2}}}\).
• (c) Show that \(\sin\theta_1=\sin\theta_2\). Conclude that \(\theta_1=\theta_2\).

Question 11.322

Here is another proof of the Reflective Property.

• (a) Figure 11.110 suggests that \(\mathcal L\) is the unique line that intersects the ellipse only in the point \(P\). Assuming this, prove that \(QF_1+QF_2 \gt PF_1+PF_2\) for all points \(Q\) on the tangent line other than \(P\).
• (b) Use the Principle of Least Distance (Example 6 in Section 4.7) to prove that \(\theta_1=\theta_2\).

Question 11.323

Show that the length \({QR}\) in Figure 11.110 is independent of the point \(P\).

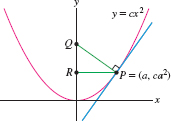
Question 11.324

Show that \({y = {x^2}/{4c}}\) is the equation of a parabola with directrix \(y=-c\), focus \((0,c)\), and the vertex at the origin, as stated in Theorem 3.

Question 11.325

Consider two ellipses in standard position: \begin{align*} E_1: \quad \left(\frac{x}{a_1}\right)^2+\left(\frac{y}{b_1}\right)^2 =1\\ E_2: \quad \left(\frac{x}{a_2}\right)^2+\left(\frac{y}{b_2}\right)^2 =1 \end{align*}

We say that \(E_1\) is similar to \(E_2\) under scaling if there exists a factor \(r \gt 0\) such that for all \((x,y)\) on \(E_1\), the point \((rx,ry)\) lies on \(E_2\). Show that \(E_1\) and \(E_2\) are similar under scaling if and only if they have the same eccentricity. Show that any two circles are similar under scaling.

Question 11.326

Derive Equations (13) and (14) in the text as follows. Write the coordinates of \(P\) with respect to the rotated axes in Figure 11.106 in polar form \(x' = r\cos\alpha\), \(y' = r\sin\alpha\). Explain why \(P\) has polar coordinates \((r,\alpha + \theta)\) with respect to the standard \(x\) and \(y\)-axes and derive (13) and (14) using the addition formulas for cosine and sine.

Question 11.327

If we rewrite the general equation of degree 2 Eq.(12) in terms of variables \(x'\) and \(y'\) that are related to \(x\) and \(y\) by Eqs.(13) and (14), we obtain a new equation of degree 2 in \(x'\) and \(y'\) of the same form but with different coefficients: \[ a'x^2+b'xy+c'y^2+d'x+e'y+f'=0 \]

• (a) Show that \({b'=b\cos 2\theta+(c-a)\sin 2\theta}\).
• (b) Show that if \(b\ne 0\), then we obtain \(b'=0\) for \[ \theta=\frac12\cot^{-1}\frac{a-c}b \]

This proves that it is always possible to eliminate the cross term \(bxy\) by rotating the axes through a suitable angle.