Question 11.328

Which of the following curves pass through the point \((1,4)\)?

• (a) \(c(t)=(t^2,t+3)\)
• (b) \(c(t)=(t^2,t-3)\)
• (c) \(c(t)=(t^2,3-t)\)
• (d) \(c(t)=(t-3,t^2)\)

Question 11.329

Find parametric equations for the line through \(P=(2,5)\) perpendicular to the line \(y=4x-3\).

Question 11.330

Find parametric equations for the circle of radius 2 with center \((1,1)\). Use the equations to find the points of intersection of the circle with the \(x\)- and \(y\)-axes.

Question 11.331

Find a parametrization \(c(t)\) of the line \(y=5-2x\) such that \(c(0)=(2,1)\).

Question 11.332

Find a parametrization \(c(\theta)\) of the unit circle such that \(c(0)=(-1,0)\).

Question 11.333

Find a path \(c(t)\) that traces the parabolic arc \(y=x^2\) from \((0,0)\) to \((3,9)\) for \(0\le t \le 1\).

Question 11.334

Find a path \(c(t)\) that traces the line \(y=2x+1\) from \((1,3)\) to \((3,7)\) for \(0\le t \le 1\).

Question 11.335

Sketch the graph \(c(t)=(1+\cos t, \sin 2t)\) for \(0\le t\le 2\pi\) and draw arrows specifying the direction of motion.

Question 11.336

\({c(t)=(4t-3,10-t)}\)

Question 11.337

\({c(t)=(t^3+1,t^2-4)}\)

Question 11.338

\(c(t)=\left(3-\dfrac{2}{t},t^3+\dfrac{1}{t}\right)\)

Question 11.339

\(x= \tan t\),\(\quad\) \(y= \sec t\)

Question 11.340

\(c(t)=(t^3+t,t^2-1)\),\(\quad\) \(t=3\)

Question 11.341

\(c(\theta)=(\tan^2\theta,\cos\theta)\),\(\quad \)\(\theta=\frac{\pi}4\)

Question 11.342

\(c(t)=(e^t-1,\sin t)\),\(\quad\) \(t=20\)

Question 11.343

\(c(t)=(\ln t,3t^2-t)\),\(\quad\) \(P=(0,2)\)

Question 11.344

Find the point on the cycloid \(c(t)=(t-\sin t,1-\cos t)\) where the tangent line has slope \(\frac12\).

Question 11.345

Find the points on \((t+\sin t,t-2\sin t)\) where the tangent is vertical or horizontal.

Question 11.346

Find the equation of the Bézier curve with control points \[ P_0=(-1,-1),\quad P_1=(-1,1),\quad P_2=(1,1),\quad P_3(1,-1) \]

Question 11.347

Find the speed at \(t=\frac{\pi}4\) of a particle whose position at time \(t\) seconds is \(c(t)=(\sin4t,\cos3t)\).

Question 11.348

Find the speed (as a function of \(t\)) of a particle whose position at time \(t\) seconds is \(c(t)=(\sin t+t,\cos t+t)\). What is the particle's maximal speed?

Question 11.349

Find the length of \((3e^t-3,4e^t+7)\) for \(0\le t\le1\).

Question 11.350

Show that \(c(t)\) for \(0\le t \lt \infty\) has finite length and calculate its value.

Question 11.351

Find the first positive value of \(t_0\) such that the tangent line to \(c(t_0)\) is vertical, and calculate the speed at \(t=t_0\).

Question 11.352

Plot \(c(t)=(\sin 2t, 2\cos t)\) for \(0\le t\le\pi\). Express the length of the curve as a definite integral, and approximate it using a computer algebra system.

Question 11.353

Convert the points \((x,y)=(1,-3)\), \((3,-1)\) from rectangular to polar coordinates.

Question 11.354

Convert the points \((r,\theta)=\bigl(1,\frac{\pi}{6}\bigr)\), \(\bigl(3,\frac{5\pi}{4}\bigr)\) from polar to rectangular coordinates.

Question 11.355

Write \((x+y)^2=xy+6\) as an equation in polar coordinates.

Question 11.356

Write \(r=\dfrac{2\cos\theta}{\cos\theta-\sin\theta}\) as an equation in rectangular coordinates.

Question 11.357

Show that \(r=\dfrac{4}{7\cos\theta-\sin\theta}\) is the polar equation of a line.

Question 11.358

Convert the equation \[ 9(x^2+y^2)=(x^2+y^2-2y)^2 \] to polar coordinates, and plot it with a graphing utility.

Question 11.359

Calculate the area of the circle \(r=3\sin\theta\) bounded by the rays \(\theta=\frac{\pi}{3}\) and \(\theta=\frac{2\pi}{3}\).

Question 11.360

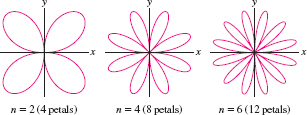
Calculate the area of one petal of \(r=\sin4\theta\) (see Figure 11.112).

Question 11.361

The equation \(r=\sin(n\theta)\), where \(n\ge 2\) is even, is a “rose” of \(2n\) petals (Figure 11.112). Compute the total area of the flower, and show that it does not depend on \(n\).

Figure 11.112: Plot of \(r=\sin(n\theta)\).

Question 11.362

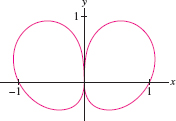
Calculate the total area enclosed by the curve \(r^2=\cos\theta e^{\sin\theta}\) (Figure 11.113).

Figure 11.113: Graph of \(r^2=\cos\theta e^{\sin\theta}\).

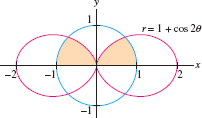
Question 11.363

Find the shaded area in Figure 11.114.

Question 11.364

Find the area enclosed by the cardioid \(r = a(1 + \cos \theta)\), where \(a \gt 0\).

Question 11.365

Calculate the length of the curve with polar equation \(r=\theta\) in Figure 11.115.

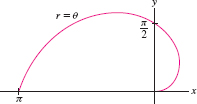
Question 11.366

Figure 11.116 shows the graph of \(r=e^{0.5\theta}\sin \theta\) for \(0\le\theta\le2\pi\). Use a computer algebra system to approximate the difference in length between the outer and inner loops.

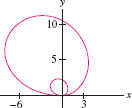
Question 11.367

Show that \(r=f_1(\theta)\) and \(r=f_2(\theta)\) define the same curves in polar coordinates if \(f_1(\theta)=-f_2(\theta+\pi)\). Use this to show that the following define the same conic section: \[ r=\frac{de}{ 1-e\cos\theta},\qquad r=\frac{-de}{1+e\cos\theta} \]

Question 11.368

\(\left(\dfrac{x}{3}\right)^2+\left(\dfrac{y}{2}\right)^2=1\)

Question 11.369

\(x^2-2y^2=4\)

Question 11.370

\(\big(2x+\frac12y\big)^2=4-(x-y)^2\)

Question 11.371

\((y-3)^2=2x^2-1\)

Question 11.372

Ellipse with vertices \((\pm8,0)\) and foci \((\pm\sqrt{3},0)\)

Question 11.373

Ellipse with foci \((\pm8,0)\), eccentricity \(\frac18\)

Question 11.374

Hyperbola with vertices \((\pm8,0)\), asymptotes \(y=\pm\tfrac{3}{4}x\)

Question 11.375

Hyperbola with foci \((2,0)\) and \((10,0)\), eccentricity \(e=4\)

Question 11.376

Parabola with focus \((8,0)\), directrix \(x=-8\)

Question 11.377

Parabola with vertex \((4,-1)\), directrix \(x=15\)

Question 11.378

Find the asymptotes of the hyperbola \(3x^2+6x-y^2-10y=1\).

Question 11.379

Show that the “conic section” with equation \(x^2-4x+y^2+5=0\) has no points.

Question 11.380

Show that the relation \({\frac{dy}{dx}=(e^2-1)\frac{x}y}\) holds on a standard ellipse or hyperbola of eccentricity \(e\).

Question 11.381

The orbit of Jupiter is an ellipse with the sun at a focus. Find the eccentricity of the orbit if the perihelion (closest distance to the sun) equals \(740\times10^6\) km and the aphelion (farthest distance from the sun) equals \(816\times10^6\) km.

Question 11.382

Refer to Figure 11.110 in Section 11.5. Prove that the product of the perpendicular distances \({F_1R_1}\) and \({F_2R_2}\) from the foci to a tangent line of an ellipse is equal to the square \(b^2\) of the semiminor axes.