11.3 EXERCISES
Preliminary Questions
Question 11.1
Describe the shape of the curve \(x=3\cos t, y = 3\sin t\).
Question 11.2
How does \(x=4+3\cos t, y = 5+3\sin t\) differ from the curve in the previous question?
Question 11.3
What is the maximum height of a particle whose path has parametric equations \(x = t^9\), \(y = 4-t^2\)?
Question 11.4
Can the parametric curve \((t, \sin t)\) be represented as a graph \(y=f(x)\)? What about \((\sin t, t)\)?
Question 11.5
Match the derivatives with a verbal description:
- \(\frac{dx}{dt}\)
- \(\frac{dy}{dt}\)
- \(\frac{dy}{dx}\)
- (i) Slope of the tangent line to the curve
- (ii) Vertical rate of change with respect to time
- (iii) Horizontal rate of change with respect to time
Exercises
Question 11.6
Find the coordinates at times \(t = 0\), 2, 4 of a particle following the path \(x=1+t^3\), \(y =9-3t^2\).
Question 11.7
Find the coordinates at \(t = 0, \frac{\pi}4, \pi\) of a particle moving along the path \(c(t)=(\cos 2t, \sin^2t)\).
Question 11.8
Show that the path traced by the bullet in Example 3 is a parabola by eliminating the parameter.
Question 11.9
Use the table of values to sketch the parametric curve \((x(t),y(t))\), indicating the direction of motion.
| \(t\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(x\) | -15 | 0 | 3 | 0 | -3 | 0 | 15 |
| \(y\) | 5 | 0 | -3 | -4 | -3 | 0 | 5 |
Question 11.10
Graph the parametric curves. Include arrows indicating the direction of motion.
- (a) \((t, t),\quad -\infty < t < \infty\)
- (b) \((\sin t,\sin t),\quad 0 \le t \le 2\pi\)
- (c) \((e^t,e^t),\quad -\infty < t < \infty\)
- (d) \((t^3,t^3),\quad -1 \le t \le 1\)
Question 11.11
Give two different parametrizations of the line through \((4,1)\) with slope \(2\).
In Exercises 7–14, express in the form \(y=f(x)\) by eliminating the parameter.
Question 11.12
\(x = t+3,\quad y = 4t\)
Question 11.13
\(x = t^{-1},\quad y=t^{-2}\)
Question 11.14
\(x = t,\quad y=\tan^{-1}(t^3+e^t)\)
Question 11.15
\(x = t^2,\quad y = t^3 + 1\)
Question 11.16
\(x = e^{-2t},\quad y = 6e^{4t}\)
Question 11.17
\(x = 1 + t^{-1},\quad y = t^2\)
Question 11.18
\(x = \ln t,\quad y = 2 - t\)
Question 11.19
\(x = \cos t,\quad y = \tan t\)
In Exercises 15–18, graph the curve and draw an arrow specifying the direction corresponding to motion.
Question 11.20
\(x=\frac12 t,\quad y = 2t^2\)
Question 11.21
\(x=2+4t,\quad y = 3+2t\)
Question 11.22
\(x=\pi t,\quad y = \sin t\)
Question 11.23
\(x=t^2,\quad y = t^3\)
Question 11.24
Match the parametrizations (a)–(d) below with their plots in Figure 11.14, and draw an arrow indicating the direction of motion.
616
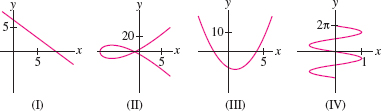
- (a) \(c(t) = (\sin t, -t)\)
- (b) \(c(t) = (t^2-9,8t-t^3)\)
- (c) \(c(t) = (1-t,t^2-9)\)
- (d) \(c(t) = (4t+2,5-3t)\)
Question 11.25
A particle follows the trajectory \[x(t) = \dfrac14 t^3 + 2t,\qquad y(t) = 20t - t^2 \] with \(t\) in seconds and distance in centimeters.
- (a) What is the particle’s maximum height?
- (b) When does the particle hit the ground and how far from the origin does it land?
Question 11.26
Find an interval of \(t\)-values such that \(c(t)=(\cos t, \sin t)\) traces the lower half of the unit circle.
Question 11.27
Find an interval of \(t\)-values such that \(c(t)=(2t+1,4t-5)\) parametrizes the segment from \((0,-7)\) to \((7,7)\).
In Exercises 23–38, find parametric equations for the given curve.
Question 11.28
\(y= 9-4x\)
Question 11.29
\(y = 8x^2-3x\)
Question 11.30
\(4x-y^2=5\)
Question 11.31
\(x^2+y^2=49\)
Question 11.32
\((x+9)^2+(y-4)^2=49\)
Question 11.33
\(\Big(\frac{x}5\Big)^2 + \Big(\frac{y}{12}\Big)^2 = 1\)
Question 11.34
Line of slope \(8\) through \((-4,9)\)
Question 11.35
Line through \((2,5)\) perpendicular to \(y=3x\)
Question 11.36
Line through \((3,1)\) and \((-5,4)\)
Question 11.37
Line through \(\big(\frac13,\frac16\big)\) and \(\big(-\frac76,\frac53\big)\)
Question 11.38
Segment joining \((1,1)\) and \((2,3)\)
Question 11.39
Segment joining \((-3,0)\) and \((0,4)\)
Question 11.40
Circle of radius 4 with center \((3,9)\)
Question 11.41
Ellipse of Exercise 28, with its center translated to \((7,4)\)
Question 11.42
\(y = x^2\), translated so that the minimum occurs at \((-4,-8)\)
Question 11.43
\(y=\cos x\) translated so that a maximum occurs at \((3,5)\)
In Exercises 39–42, find a parametrization \(c(t)\) of the curve satisfying the given condition.
Question 11.44
\(y=3x-4,\quad c(0)=(2,2)\)
Question 11.45
\(y=3x-4,\quad c(3)=(2,2)\)
Question 11.46
\(y=x^2,\quad c(0)=(3,9)\)
Question 11.47
\(x^2+y^2=4,\quad c(0)=\big(\frac12,\frac{\sqrt{3}}2\big)\)
Question 11.48
Describe \(c(t) = (\sec t, \tan t)\) for \(0\le t <\frac{\pi}2\) in the form \(y=f(x)\). Specify the domain of \(x\).
Question 11.49
Find a parametrization of the right branch (\(x>0\)) of the hyperbola \[ \left(\dfrac{x}{a}\right)^2-\left(\dfrac{y}{b}\right)^2=1 \] using the functions \(\cosh t\) and \(\sinh t\). How can you parametrize the branch \(x<0\)?
Question 11.50
The graphs of \(x(t)\) and \(y(t)\) as functions of \(t\) are shown in Figure 11.15. Which of (I)–(III) is the plot of \(c(t)=(x(t),y(t))\)? Explain.

Question 11.51
Which graph, (I) or (II), is the graph of \(x(t)\) and which is the graph of \(y(t)\) for the parametric curve in Figure 11.16?
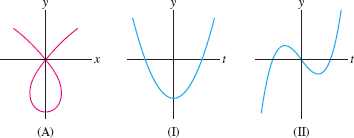
Question 11.52
Sketch \(c(t) = (t^3 - 4t, t^2)\) following the steps in Example 7.
Question 11.53
Sketch \(c(t) = (t^2 - 4t, 9 - t^2)\) for \(-4\le t \le 10\).
In Exercises 49–52, use Eq. (7) to find \(dy/dx\) at the given point.
Question 11.54
\((t^3, t^2 - 1),\quad t = -4\)
Question 11.55
\((2t+9, 7t-9),\quad t = 1\)
Question 11.56
\((s^{-1}-3s, s^3),\quad s = -1\)
Question 11.57
\((\sin 2\theta, \cos 3\theta),\quad \theta = \frac{\pi}6\)
In Exercises 53–56, find an equation \(y = f(x)\) for the parametric curve and compute \({dy}/dx\) in two ways: using Eq. (7) and by differentiating \(f(x)\).
Question 11.58
\(c(t)=(2t+1, 1-9t)\)
Question 11.59
\(c(t)=\bigl(\frac{1}{2}t, \frac14t^2 - t\bigr)\)
Question 11.60
\(x = s^3,\quad y = s^6+s^{-3}\)
617
Question 11.61
\(x = \cos \theta,\quad y = \cos\theta + \sin^2\theta\)
Question 11.62
Find the points on the curve \(c(t) = (3t^2-2t,t^3-6t)\) where the tangent line has slope \(3\).
Question 11.63
Find the equation of the tangent line to the cycloid generated by a circle of radius \(4\) at \(t=\frac{\pi}2\).
In Exercises 59–62, let \(c(t) = (t^2 - 9, t^2 - 8t)\) (see Figure 11.17).
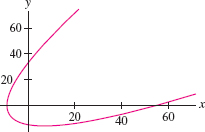
Question 11.64
Draw an arrow indicating the direction of motion, and determine the interval of \(t\)-values corresponding to the portion of the curve in each of the four quadrants.
Question 11.65
Find the equation of the tangent line at \(t = 4\).
Question 11.66
Find the points where the tangent has slope \(\frac12\).
Question 11.67
Find the points where the tangent is horizontal or vertical.
Question 11.68
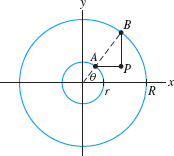
Let \(A\) and \(B\) be the points where the ray of angle \(\theta\) intersects the two concentric circles of radii \(r<R\) centered at the origin (Figure 11.18). Let \(P\) be the point of intersection of the horizontal line through \(A\) and the vertical line through \(B\). Express the coordinates of \(P\) as a function of \(\theta\) and describe the curve traced by \(P\) for \(0\le \theta \le 2\pi\).
Question 11.69
A 10-ft ladder slides down a wall as its bottom \(B\) is pulled away from the wall (Figure 11.19). Using the angle \(\theta\) as parameter, find the parametric equations for the path followed by (a) the top of the ladder \(A\), (b) the bottom of the ladder \(B\), and (c) the point \(P\) located 4 ft from the top of the ladder. Show that \(P\) describes an ellipse.

In Exercises 65–68, refer to the Bézier curve defined by Eqs. (8) and (9).
Question 11.70
Show that the Bézier curve with control points \[ P_0 = (1, 4),\quad P_1 =(3, 12),\quad P_2 =(6, 15),\quad P_3 =(7, 4) \] has parametrization \[ c(t) = (1 + 6t + 3t^2 - 3t^3, 4 + 24t - 15t^2 - 9t^3) \] Verify that the slope at \(t=0\) is equal to the slope of the segment \(\overline{P_0P_1}\).
Question 11.71
Find an equation of the tangent line to the Bézier curve in Exercise 65 at \(t = \frac13\).
Question 11.72
![]() Find and plot the Bézier curve \(c(t)\) passing
through the control points
\[
P_0 = (3, 2),\quad P_1 =(0, 2),\quad P_2 =(5,4),\quad P_3 =(2, 4)
\]
Find and plot the Bézier curve \(c(t)\) passing
through the control points
\[
P_0 = (3, 2),\quad P_1 =(0, 2),\quad P_2 =(5,4),\quad P_3 =(2, 4)
\]
Question 11.73
Show that a cubic Bézier curve is tangent to the segment \(\overline{P_2P_3}\) at \(P_3\).
Question 11.74
A bullet fired from a gun follows the trajectory \[ x = at,\qquad y = bt - 16t^2 \quad (a,b>0) \] Show that the bullet leaves the gun at an angle \(\theta = \tan^{-1}\big(\tfrac{b}{a}\big)\) and lands at a distance \({ab}/{16}\) from the origin.
Question 11.75
![]() Plot \(c(t)= (t^3 - 4t, t^4 - 12t^2 + 48)\)
for \(-3\le t \le 3\). Find the points where the tangent line is
horizontal or vertical.
Plot \(c(t)= (t^3 - 4t, t^4 - 12t^2 + 48)\)
for \(-3\le t \le 3\). Find the points where the tangent line is
horizontal or vertical.
Question 11.76
![]() Plot the astroid \(x = \cos^3\theta\), \(y = \sin^3\theta\)
and find the equation of the tangent line at \(\theta
=\frac{\pi}3\).
Plot the astroid \(x = \cos^3\theta\), \(y = \sin^3\theta\)
and find the equation of the tangent line at \(\theta
=\frac{\pi}3\).
Question 11.77
Find the equation of the tangent line at \(t=\frac{\pi}4\) to the cycloid generated by the unit circle with parametric equation (5).
Question 11.78
Find the points with horizontal tangent line on the cycloid with parametric equation (5).
618
Question 11.79
Property of the Cycloid Prove that the tangent line at a point \(P\) on the cycloid always passes through the top point on the rolling circle as indicated in Figure 11.20. Assume the generating circle of the cycloid has radius 1.
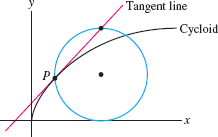
Question 11.80
A curtate cycloid (Figure 11.21) is the curve traced by a point at a distance \(h\) from the center of a circle of radius \(R\) rolling along the \(x\)-axis where \(h<R\). Show that this curve has parametric equations \(x = Rt - h \sin t\), \(y = R - h \cos t\).
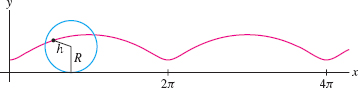
Question 11.81
![]() Use a computer algebra system to explore what happens when \(h>R\) in the parametric equations of Exercise 75. Describe the result.
Use a computer algebra system to explore what happens when \(h>R\) in the parametric equations of Exercise 75. Describe the result.
Question 11.82
![]() Show that the line of slope \(t\) through \((-1,0)\)
intersects the unit circle in the point with coordinates
\begin{equation}
\label{12.exparam.parcir}
x = \frac{1 - t^2}{t^2 + 1}, \qquad y = \frac{2t}{t^2 + 1}\tag{10}
\end{equation}
Show that the line of slope \(t\) through \((-1,0)\)
intersects the unit circle in the point with coordinates
\begin{equation}
\label{12.exparam.parcir}
x = \frac{1 - t^2}{t^2 + 1}, \qquad y = \frac{2t}{t^2 + 1}\tag{10}
\end{equation}
Conclude that these equations parametrize the unit circle with the point \((-1,0)\) excluded (Figure 11.22). Show further that \(t = {y}/({x+1})\).
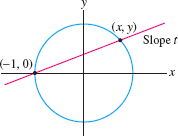
Question 11.83
The folium of Descartes is the curve with equation \(x^3+y^3=3axy\), where \(a\ne 0\) is a constant (Figure 11.23).
- (a) Show that the line \(y=tx\) intersects the folium at the origin and at one other point \(P\) for all \(t\neq -1, 0\). Express the coordinates of \(P\) in terms of \(t\) to obtain a parametrization of the folium. Indicate the direction of the parametrization on the graph.
- (b) Describe the interval of \(t\)-values parametrizing the parts of the curve in quadrants I, II, and IV. Note that \(t=-1\) is a point of discontinuity of the parametrization.
- (c) Calculate \(dy/dx\) as a function of \(t\) and find the points with horizontal or vertical tangent.
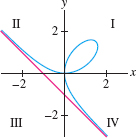
Question 11.84
Use the results of Exercise 78 to show that the asymptote of the folium is the line \(x+y=- a\). Hint: Show that \(\lim\limits_{t\to -1}(x+y)=-a\).
Question 11.85
Find a parametrization of \(x^{2n+1}+y^{2n+1}=ax^ny^n\), where \(a\) and \(n\) are constants.
Question 11.86
Second Derivative for a Parametrized Curve Given a parametrized curve \(c(t)=(x(t), y(t))\), show that \[ \frac{d}{dt}\Big(\frac{dy}{dx}\Big) = \frac{x'(t)y''(t)-y'(t)x''(t)}{x'(t)^2} \]
Use this to prove the formula \[ \boxed{\bbox[#fef7e5,5pt]{\frac{d^2y}{dx^2} = \frac{x'(t)y''(t)-y'(t)x''(t)}{x'(t)^3}}}\tag{11} \]
Question 11.87
The second derivative of \(y=x^2\) is \({dy^2}{d^2x}=2\). Verify that Eq. (11) applied to \(c(t)=(t,t^2)\) yields \({dy^2}{d^2x}=2\). In fact, any parametrization may be used. Check that \(c(t)=(t^3,t^6)\) and \(c(t) = (\tan t,\tan^2 t)\) also yield \({dy^2}{d^2x}=2\).
In Exercises 83–86, use Eq. (11) to find \({d^2y}/{dx^2}\).
Question 11.88
\(x=t^3+t^2,\quad y = 7t^2-4,\quad t = 2\)
Question 11.89
\(x=s^{-1}+s,\quad y = 4-s^{-2},\quad s = 1\)
Question 11.90
\(x=8t+9,\quad y = 1-4t,\quad t = -3\)
Question 11.91
\(x=\cos \theta,\quad y = \sin \theta,\quad \theta = \frac{\pi}{4}\)
Question 11.92
Use Eq. (11) to find the \(t\)-intervals on which \(c(t) =(t^2, t^3 - 4t)\) is concave up.
Question 11.93
Use Eq. (11) to find the \(t\)-intervals on which \(c(t) =(t^2, t^4 - 4t)\) is concave up.
619
Question 11.94
Area Under a Parametrized Curve Let \(c(t)=(x(t),y(t))\), where \(y(t)>0\) and \(x'(t)>0\) (Figure 11.24). Show that the area \(A\) under \(c(t)\) for \(t_0\le t\le t_1\) is \begin{equation} \label{12.exparam.paramarea} A = \int_{t_0}^{t_1} y(t)x'(t)\,dt\tag{12} \end{equation}
Hint: Because it is increasing, the function \(x(t)\) has an inverse \(t = g(x)\) and \(c(t)\) is the graph of \(y = y(g(x))\). Apply the change-of-variables formula to \({A = \int_{x(t_0)}^{x(t_1)} y(g(x))\,dx}\).

Question 11.95
Calculate the area under \(y=x^2\) over \(\left[0,1\right]\) using Eq. (12) with the parametrizations \((t^3,t^6)\) and \((t^2,t^4)\).
Question 11.96
What does Eq. (12) say if \(c(t) = (t,f(t))\)?
Question 11.97
Sketch the graph of \(c(t)=(\ln t, 2 - t)\) for \(1\le t\le 2\) and compute the area under the graph using Eq. (12).
Question 11.98
Galileo tried unsuccessfully to find the area under a cycloid. Around 1630, Gilles de Roberval proved that the area under one arch of the cycloid \(c(t) = (Rt-R\sin t, R-R\cos t)\) generated by a circle of radius \(R\) is equal to three times the area of the circle (Figure 11.25). Verify Roberval’s result using Eq. (12).

Further Insights and Challenges
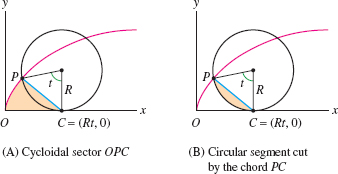
Question 11.99
Prove the following generalization of Exercise 93: For all \(t>0\), the area of the cycloidal sector \(OPC\) is equal to three times the area of the circular segment cut by the chord \(PC\) in Figure 11.26.
Question 11.100
![]() Derive the formula for the slope
of the tangent line to a parametric curve \(c(t)=(x(t), y(t))\) using
a method different from that presented in the text. Assume that
\(x'(t_0)\) and \(y'(t_0)\) exist and that \(x'(t_0)\ne 0\). Show that
\[
\lim_{h\to 0}
\frac{y(t_0+h)-y(t_0)}{x(t_0+h)-x(t_0)}=\frac{y'(t_0)}{x'(t_0)}
\]
Derive the formula for the slope
of the tangent line to a parametric curve \(c(t)=(x(t), y(t))\) using
a method different from that presented in the text. Assume that
\(x'(t_0)\) and \(y'(t_0)\) exist and that \(x'(t_0)\ne 0\). Show that
\[
\lim_{h\to 0}
\frac{y(t_0+h)-y(t_0)}{x(t_0+h)-x(t_0)}=\frac{y'(t_0)}{x'(t_0)}
\]
Then explain why this limit is equal to the slope \(dy/dx\). Draw a diagram showing that the ratio in the limit is the slope of a secant line.
Question 11.101
Verify that the tractrix curve \((\ell>0)\) \[ c(t) = \left(t-\ell\tanh \frac{t}{\ell}, \ell \textrm{sech } \frac{t}{\ell}\right) \] has the following property: For all \(t\), the segment from \(c(t)\) to \((t,0)\) is tangent to the curve and has length \(\ell\) (Figure 11.27).

Question 11.102
In Exercise 54 of Section 9.1, we described the tractrix by the differential equation \[ \frac{dy}{dx}=-\frac{y}{\sqrt{\ell^2-y^2}} \]
Show that the curve \(c(t)\) identified as the tractrix in Exercise 96 satisfies this differential equation. Note that the derivative on the left is taken with respect to \(x\), not \(t\).
In Exercises 98 and 99, refer to Figure 11.28.
Question 11.103
In the parametrization \(c(t)= (a\cos t, b\sin t)\) of an ellipse, \(t\) is not an angular parameter unless \(a=b\) (in which case the ellipse is a circle). However, \(t\) can be interpreted in terms of area: Show that if \(c(t)= (x,y)\), then \(t = (2/ab)A\), where \(A\) is the area of the shaded region in Figure 11.28. Hint: Use Eq. (12).
620

Question 11.104
Show that the parametrization of the ellipse by the angle \(\theta\) is \begin{align*} x &= \frac{ab\cos\theta}{\sqrt{a^2\sin^2\theta+b^2\cos^2\theta}}\\ y&=\frac{ab\sin\theta}{\sqrt{a^2\sin^2\theta+b^2\cos^2\theta}} \end{align*}