11.4 Arc Length and Speed
We now derive a formula for the arc length of a curve in parametric form. Recall that in Section 8.1, arc length was defined as the limit of the lengths of polygonal approximations (Figure 11.29).
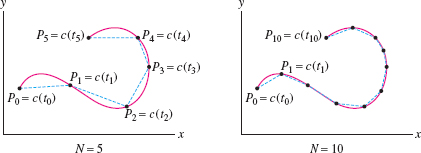
Given a parametrization \(c(t)=(x(t), y(t))\) for \(a\le t\le b\), we construct a polygonal approximation \(L\) consisting of the \(N\) segments by joining points \[ P_0= c(t_0),\quad P_1 = c(t_1),\quad \ldots , \quad P_N = c(t_N) \] corresponding to a choice of values \(t_0=a < t_1 < t_2 < \cdots < t_N=b\). By the distance formula, \begin{equation} \label{12.length.polyapp} P_{i-1}P_i = \sqrt{ \big(x(t_i)-x(t_{i-1})\big)^2+\big(y(t_i)-y(t_{i-1})\big)^2}\tag{1} \end{equation}
Now assume that \(x(t)\) and \(y(t)\) are differentiable. According to the Mean Value Theorem, there are values \(t_i^*\) and \(t_i^{**}\) in the interval \([t_{i-1},t_i]\) such that \[ x(t_i)-x(t_{i-1})= x'(t_i^*)\Delta t_i, \qquad y(t_i)-y(t_{i-1})= y'(t_i^{**})\Delta t_i \] where \(\Delta t_i = t_i-t_{i-1}\), and therefore, \begin{align*} P_{i-1}P_i & = \sqrt{ x'(t_i^*)^2\Delta t_i^2+ y'(t_i^{**})^2\Delta t_i^2} = \sqrt{ x'(t_i^*)^2 + y'(t_i^{**})^2 }\,\Delta t_i \end{align*} The length of the polygonal approximation \(L\) is equal to the sum \begin{equation} \label{12.length.sum} \sum_{i=1}^N P_{i-1}P_i = \sum_{i=1}^N \sqrt{ x'(t_i^*)^2 + y'(t_i^{**})^2 }\,\Delta t_i\tag{2} \end{equation}
This is nearly a Riemann sum for the function \(\sqrt{ x'(t)^2 + y'(t)^2 }\). It would be a true Riemann sum if the intermediate values \(t_i^*\) and \(t_i^{**}\) were equal. Although they are not necessarily equal, it can be shown (and we will take for granted) that if \(x'(t)\) and \(y'(t)\) are continuous,
621
then the sum in Eq. (2) still approaches the integral as the widths \(\Delta t_i\) tend to \(0\). Thus, \[ s = \lim\,\sum_{i=1}^N P_{i-1}P_i = \int_a^b \sqrt{ x'(t)^2 + y'(t)^2 }\, dt \]
Note
Because of the square root, the arc length integral cannot be evaluated explicitly except in special cases, but we can always approximate it numerically.
THEOREM 1 Arc Length
Let \(c(t)=(x(t),y(t))\), where \(x'(t)\) and \(y'(t)\) exist and are continuous. Then the arc length \(s\) of \(c(t)\) for \(a\le t\le b\) is equal to \begin{equation} \label{12.length.formula} s = \int_a^b \sqrt{x'(t)^2 + y'(t)^2}\, dt\tag{3} \end{equation}
The graph of a function \(y=f(x)\) has parametrization \(c(t) = (t,f(t))\). In this case, \[{\sqrt{x'(t)^2 + y'(t)^2}=\sqrt{1 + f'(t)^2}}\] and Eq (3) reduces to the arc length formula derived in Section 8.1.
As mentioned above, the arc length integral can be evaluated explicitly only in special cases. The circle and the cycloid are two such cases.
EXAMPLE 1
Use Eq. 3 to calculate the arc length of a circle of radius \(R\).
Solution With the parametrization \(x=R\cos\theta\), \(y=R\sin\theta\), \begin{align*} x'(\theta)^2+y'(\theta)^2 &= (-R\sin\theta)^2 + (R\cos\theta)^2 = R^2(\sin^2\theta+\cos^2\theta) = R^2 \end{align*}
We obtain the expected result: \begin{align*} s &= \int_{0}^{2\pi} \sqrt{x'(\theta)^2+y'(\theta)^2}\, d\theta = \int_{0}^{2\pi} R\, d\theta = 2\pi R \end{align*}
EXAMPLE 2 Length of the Cycloid
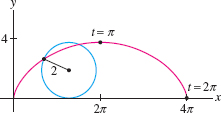
Calculate the length \(s\) of one arch of the cycloid generated by a circle of radius \(R=2\) (Figure 11.30).
REMINDER
\[ \frac{1-\cos t}2 = \sin^2\frac{t}2 \]
Solution We use the parametrization of the cycloid in Eq. (6) of Section 1: \begin{align*} x(t) &= 2(t - \sin t),& y(t) &= 2(1 - \cos t)\\ x'(t) &= 2(1 -\cos t), & y'(t)&=2 \sin t \end{align*} Thus, \begin{align*} x'(t)^2+y'(t)^2 &= 2^2(1-\cos t)^2+2^2\sin^2t\\ & = 4 - 8\cos t + 4\cos^2t+4\sin^2t \\ &= 8 -8\cos t\\ &=16\sin^2\frac{t}2\qquad\textrm{(Use the identity recalled in the margin.)} \end{align*}
One arch of the cycloid is traced as \(t\) varies from 0 to \(2\pi\), and thus \[ s = \int_{0}^{2\pi} \sqrt{x'(t)^2+y'(t)^2}\, dt = \int_{0}^{2\pi} 4 \sin \frac{t}2 \, dt = -8\cos\frac{t}2\bigg|_0^{2\pi}= -8(-1)+8 = 16 \]
Note that because \(\sin \tfrac{t}2\ge 0\) for \(0\le t\le 2\pi\), we did not need an absolute value when taking the square root of \(16\sin^2\tfrac{t}2\).
622
Now consider a particle moving along a path \(c(t)\). The distance traveled by the particle over the time interval \([t_0,t]\) is given by the arc length integral: \[ s(t) = \int_{t_0}^t \sqrt{x'(u)^2+y'(u)^2}\, du \]
Note
In Chapter 13, we will discuss not just the speed but also the velocity of a particle moving along a curved path. Velocity is “speed plus direction” and is represented by a vector.
On the other hand, speed is defined as the rate of change of distance traveled with respect to time, so by the Fundamental Theorem of Calculus, \[ \textrm{Speed} = \frac{ds}{dt} = \frac{d}{dt} \int_{t_0}^t \sqrt{x'(u)^2+y'(u)^2}\, du = \sqrt{x'(t)^2+y'(t)^2} \]
THEOREM 2 Speed Along a Parametrized Path
The speed of \(c(t)=(x(t), y(t))\) is \[ \boxed{\bbox[#fef7e5,5pt]{ \mathrm{Speed} = \frac{ds}{dt} = \sqrt{x'(t)^2 + y'(t)^2} }}\]
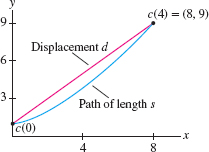
The next example illustrates the difference between distance traveled along a path and displacement (also called net change in position). The displacement along a path is the distance between the initial point \(c(t_0)\) and the endpoint \(c(t_1)\). The distance traveled is greater than the displacement unless the particle happens to move in a straight line (Figure 11.31).

EXAMPLE 3
A particle travels along the path \(c(t) = (2t,1+t^{3/2})\). Find:
- (a) The particle’s speed at \(t=1\) (assume units of meters and minutes).
- (b) The distance traveled \(s\) and displacement \(d\) during the interval \(0\le t\le 4\).
Solution We have \begin{align*} x'(t) &= 2,\qquad y'(t) = \frac32t^{1/2} \end{align*}
The speed at time \(t\) is \begin{align*} s'(t) &= \sqrt{x'(t)^2+y'(t)^2} = \sqrt{4 + \frac94t} \quad\text{m/min} \end{align*}
- (a) The particle’s speed at \(t=1\) is \(s'(1)= \sqrt{4+ \frac94}= 2.5 \text{m/min}\).
- (b) The distance traveled in the first 4 min is \[ s = \int_0^4 \sqrt{4+ \frac94t}\, dt = \frac8{27}\left(4+ \frac94t\right)^{3/2}\bigg|_0^4 = \frac{8}{27}\bigl(13^{3/2} - 8\bigr) \approx 11.52 \mathrm{m} \]
The displacement \(d\) is the distance from the initial point \(c(0)=(0,1)\) to the endpoint \(c(4)=(8,1+4^{3/2})=(8,9)\) (see Figure 4): \[ d = \sqrt{(8-0)^2+(9-1)^2} =8\sqrt 2 \approx 11.31 \mathrm{m} \]
In physics,we often describe the path of a particle moving with constant speed along a circle of radius \(R\) in terms of a constant \(\omega\) (lowercase Greek omega) as follows: \[ c(t) = (R\cos\omega t,R\sin\omega t) \]
The constant \(\omega\), called the angular velocity, is the rate of change with respect to time of the particle’s angle \(\theta\) (Figure 11.33).
623
EXAMPLE 4 Angular Velocity
Calculate the speed of the circular path of radius \(R\) and angular velocity \(\omega\). What is the speed if \(R=3\) m and \(\omega = 4\) rad/s?

Solution We have \(x=R\cos\omega t\) and \(y=R\sin\omega t\), and \[ x'(t)=-\omega R\sin \omega t,\qquad y'(t)= \omega R\cos \omega t \]
The particle’s speed is \begin{align*} \frac{ds}{dt} &= \sqrt{x'(t)^2+y'(t)^2} = \sqrt{(-\omega R\sin \omega t)^2+(\omega R\cos \omega t)^2}\\ & = \sqrt{\omega^2 R^2(\sin^2\omega t+\cos^2\omega t)} = |\omega| R \end{align*}
Thus, the speed is constant with value \(|\omega|R\). If \(R=3\) m and \(\omega = 4\) rad/s, then the speed is \(|\omega| R = 3(4) = 12 \text{m/s}\).
Consider the surface obtained by rotating a parametric curve \(c(t)=(x(t),y(t))\) about the \(x\)-axis. The surface area is given by Eq. (4) in the next theorem. It can be derived in much the same way as the formula for a surface of revolution of a graph \(y=f(x)\) in Section 8.1. In this theorem, we assume that \(y(t)\ge 0\) so that the curve \(c(t)\) lies above the \(x\)-axis, and that \(x(t)\) is increasing so that the curve does not reverse direction.
THEOREM 3 Surface Area
Let \(c(t)=(x(t),y(t))\), where \(y(t)\ge 0\), \(x(t)\) is increasing, and \(x'(t)\) and \(y'(t)\) are continuous. Then the surface obtained by rotating \(c(t)\) about the \(x\)-axis for \(a\le t \le b\) has surface area \begin{equation} \label{surfareaformula} S = 2\pi \int_a^b y(t)\sqrt{x'(t)^2+y'(t)^2}\,dt\tag{4} \end{equation}
EXAMPLE 5
Calculate the surface area of the surface obtained by rotating the tractrix \(c(t)=(t-\tanh t, \textrm{sech } t)\) about the \(x\)-axis for \(0 ≤ t < \infty\).
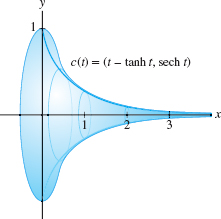
Solution Note that the surface extends infinitely to the right (Figure 11.34). We have \[ x'(t) = \frac{d}{dt}(t-\tanh t) = 1-\textrm{sech }^2t,\qquad y'(t)=\frac{d}{dt}\textrm{sech } t = -\textrm{sech } t\tanh t \]
Using the identities \(1 - \textrm{sech }^2 t = \tanh^2 t\) and \(\textrm{sech }^2t=1-\tanh^2t\), we obtain \begin{align*} x'(t)^2+y'(t)^2 &= (1-\textrm{sech }^2t)^2 +(-\textrm{sech } t\tanh t)^2 \\ &= (\tanh^2t)^2 +(1-\tanh^2t)\tanh^2t=\tanh^2t \end{align*}
REMINDER
\begin{align*} \textrm{sech } t &= \frac1{\cosh t}=\frac{2}{e^t+e^{-t}}\\ 1-\textrm{sech }^2t&=\tanh^2t\\ \frac{d}{dt}\tanh t &= \textrm{sech }^2 t\\ \frac{d}{dt}\textrm{sech } t &= -\textrm{sech } t\tanh t\\ \int \textrm{sech } t\tanh t\,dt & = -\textrm{sech } t+C \end{align*}
The surface area is given by an improper integral, which we evaluate using the integral formula recalled in the margin: \begin{align*} S &= 2\pi\int_0^{\infty} \textrm{sech } t\sqrt{\tanh^2t} \,dt=2\pi\int_0^{\infty} \textrm{sech } t \tanh t \,dt=2\pi\lim_{R\to\infty} \int_0^R \textrm{sech } t \tanh t \,dt\\ &=2\pi\lim_{R\to\infty} (-\textrm{sech } t)\Big|_0^R = 2\pi \lim_{R\to\infty}(\textrm{sech } 0 - \textrm{sech } R)=2\pi\textrm{sech } 0 = 2\pi \end{align*}
Here we use that \(\textrm{sech } R = \frac1{e^R+e^{-R}}\) tends to zero (because \(e^R\to\infty\) while \(e^{-R}\to 0\)).