Question 11.105

What is the definition of arc length?

Question 11.106

What is the interpretation of \(\sqrt{x'(t)^2 + y'(t)^2}\) for a particle following the trajectory \((x(t),y(t))\)?

Question 11.107

A particle travels along a path from \((0,0)\) to \((3,4)\). What is the displacement? Can the distance traveled be determined from the information given?

Question 11.108

A particle traverses the parabola \(y=x^2\) with constant speed \(3 \text{cm/s}\). What is the distance traveled during the first minute? Hint: No computation is necessary.

Question 11.109

\((3t+1,9-4t),\quad 0\le t\le 2\)

Question 11.110

\((1+2t,2+4t),\quad 1\le t \le 4\)

Question 11.111

\((2t^2,3t^2 - 1),\quad 0\le t\le 4\)

Question 11.112

\((3t, 4t^{3/2}),\quad 0\le t\le 1\)

Question 11.113

\((3t^2,4t^3),\quad 1\le t\le 4\)

Question 11.114

\((t^3 +1, t^2 - 3),\quad 0 \le t \le 1\)

Question 11.115

\((\sin 3t,\cos 3t),\quad 0 \le t \le \pi\)

Question 11.116

\((\sin\theta-\theta\cos\theta, \cos\theta+\theta\sin\theta),\quad 0\le \theta\le 2\)

Question 11.117

\((2\cos t - \cos 2t, 2\sin t - \sin 2t),\quad 0\le t\le \frac{\pi}2\)

Question 11.118

\((5(\theta - \sin \theta), 5(1 - \cos \theta)),\quad 0\le \theta\le 2\pi\)

Question 11.119

Show that one arch of a cycloid generated by a circle of radius \(R\) has length \(8R\).

Question 11.120

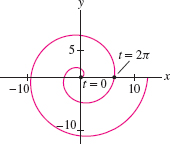
Find the length of the spiral \(c(t)= (t\cos t, t\sin t)\) for \(0\le t \le 2\pi\) to three decimal places (Figure 11.35). Hint: Use the formula \[ \int\sqrt{1+t^2}\,dt = \frac12t\sqrt{1+t^2}+\frac12 \ln\bigl(t+\sqrt{1+t^2}\bigr) \]

Figure 11.35: The spiral \(c(t)= (t\cos t, t\sin t)\).

Question 11.121

Find the length of the tractrix (see Figure 11.34) \[ c(t) = (t- \tanh(t), \textrm{sech }(t)), \qquad 0\le t\le A \]

Question 11.122

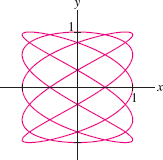
Find a numerical approximation to the length of \(c(t) = (\cos 5t, \sin 3t)\) for \(0\le t \le 2\pi\) (Figure 11.36).

Question 11.123

\((t^3,t^2),\quad t=2\)

Question 11.124

\((3\sin 5t,8\cos 5t),\quad t=\frac{\pi}4\)

Question 11.125

\((5t+1,4t-3),\quad t = 9\)

Question 11.126

\((\ln(t^2+1),t^3),\quad t = 1\)

Question 11.127

Find the minimum speed of a particle with trajectory \(c(t)=(t^3 - 4t, t^2 + 1)\) for \(t\ge 0\). Hint: It is easier to find the minimum of the square of the speed.

Question 11.128

Find the minimum speed of a particle with trajectory \(c(t)=(t^3,t^{-2})\) for \(t \ge 0.5\).

Question 11.129

Find the speed of the cycloid \(c(t) = (4t - 4\sin t, 4 - 4\cos t)\) at points where the tangent line is horizontal.

Question 11.130

Calculate the arc length integral \(s(t)\) for the logarithmic spiral \(c(t) = (e^t\cos t, e^t\sin t)\).

Question 11.131

\(c(t) = (\cos t, e^{\sin t})\quad\) for \(0\le t\le 2\pi\)

Question 11.132

\(c(t) = (t - \sin 2t, 1 - \cos 2t)\quad\) for \(0\le t\le 2\pi\)

Question 11.133

The ellipse \(\left(\frac{x}5\right)^2 + \left(\frac{y}3\right)^2 = 1\)

Question 11.134

\(x=\sin 2t,\quad y = \sin 3t\quad\) for \(0\le t\le 2\pi\)

Question 11.135

If you unwind thread from a stationary circular spool, keeping the thread taut at all times, then the endpoint traces a curve \(C\) called the involute of the circle (Figure 11.37). Observe that \(\overline{PQ}\) has length \(R\theta\). Show that \(C\) is parametrized by \[ c(\theta) = \bigl(R(\cos\theta+\theta\sin\theta),R(\sin\theta-\theta\cos\theta)\bigr) \] Then find the length of the involute for \(0\le \theta\le 2\pi\).

Figure 11.37: Involute of a circle.

Question 11.136

Let \(a>b\) and set \[{k=\sqrt{1-\frac{b^2}{a^2}}}\] Use a parametric representation to show that the ellipse \(\big(\tfrac{x}a\big)^2+\)\linebreak \(\big(\tfrac{y}b\big)^2=1\) has length \(L=4aG\bigl(\frac{\pi}2,k\bigr)\), where \[ G(\theta,k)=\int_0^{\theta}\sqrt{1-k^2\sin^2t}\, dt \] is the elliptic integral of the second kind.

Question 11.137

The cone generated by revolving \(c(t)=(t,mt)\) about the \(x\)-axis for \(0\le t \le A\)

Question 11.138

A sphere of radius \(R\)

Question 11.139

The surface generated by revolving one arch of the cycloid \(c(t)=(t-\sin t,1-\cos t)\) about the \(x\)-axis

Question 11.140

The surface generated by revolving the astroid \(c(t)=(\cos^3t,\sin^3t)\) about the \(x\)-axis for \(0\le t\le \frac{\pi}2\)

Question 11.141

Let \(b(t)\) be the “Butterfly Curve”: \begin{align*} x(t) &= \sin t \left(e^{\cos t} - 2\cos 4t - \sin\left(\frac{t}{12}\right)^5\right)\\ y(t) &= \cos t \left(e^{\cos t} - 2\cos 4t - \sin\left(\frac{t}{12}\right)^5\right) \end{align*}

• (a) Use a computer algebra system to plot \(b(t)\) and the speed \(s'(t)\) for \(0\le t \le 12\pi\).
• (b) Approximate the length \(b(t)\) for \(0\le t \le 10\pi\).

Question 11.142

Let \(a\ge b>0\) and set \(k = \frac{2\sqrt{ab}}{a-b}\). Show that the trochoid \[ x=at-b\sin t,\qquad y=a-b\cos t,\quad 0\le t \le T \] has length \(2(a-b)G\big(\tfrac{T}2,k\big)\) with \(G(\theta, k)\) as in Exercise 28.

Question 11.143

A satellite orbiting at a distance \(R\) from the center of the earth follows the circular path \(x=R\cos\omega t\), \(y=R\sin\omega t\).

• (a) Show that the period \(T\) (the time of one revolution) is \(T=2\pi/\omega\).
• (b) According to Newton’s laws of motion and gravity, \[ x''(t) = -Gm_e\frac{x}{R^3},\qquad y''(t) = -Gm_e \frac{y}{R^3} \] where \(G\) is the universal gravitational constant and \(m_e\) is the mass of the earth. Prove that \({R^3}/{T^2} = {Gm_e}/{4\pi^2}\). Thus, \({R^3}/{T^2}\) has the same value for all orbits (a special case of Kepler’s Third Law).

Question 11.144

The acceleration due to gravity on the surface of the earth is \[g = \frac{Gm_e}{R_e^2} = 9.8 \text{m/s}^2,\quad \text{where \(R_e = 6378\) km}\] Use Exercise 35(b) to show that a satellite orbiting at the earth’s surface would have period \(T_e=2\pi\sqrt{R_e/g}\approx 84.5\) min. Then estimate the distance \(R_m\) from the moon to the center of the earth. Assume that the period of the moon (sidereal month) is \(T_m\approx 27.43\) days.