12.8 Cylindrical and Spherical Coordinates
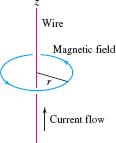
This section introduces two generalizations of polar coordinates to \(\textbf{R}^3\): cylindrical and spherical coordinates. These coordinate systems are commonly used in problems having symmetry about an axis or rotational symmetry. For example, the magnetic field generated by a current flowing in a long, straight wire is conveniently expressed in cylindrical coordinates (Figure 12.79). We will also see the benefits of cylindrical and spherical coordinates when we study change of variables for multiple integrals.
Cylindrical Coordinates
In cylindrical coordinates, we replace the \(x\)- and \(y\)-coordinates of a point \(P=(x,y,z)\) by polar coordinates. Thus, the cylindrical coordinates of \(P\) are \((r,\theta,z)\), where \((r,\theta)\) are polar coordinates of the projection \(Q = (x,y,0)\) of \(P\) onto the \(xy\)-plane (Figure 12.80). Note that the points at fixed distance \(r\) from the \(z\)-axis make up a cylinder, hence the name cylindrical coordinates.
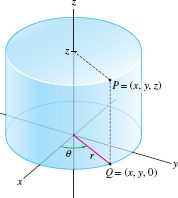
We convert between rectangular and cylindrical coordinates using the rectangular-polar formulas of Section 11.3. In cylindrical coordinates, we usually assume \(r\ge 0\).
| Cylindrical to rectangular | Rectangular to cylindrical |
| \({x=r\cos\theta}\) | \({r=\sqrt{x^2+y^2}}\) |
| \({y = r\sin\theta}\) | \({\tan\theta=\frac{y}{x}}\) |
| \({z = z}\) | \({z=z}\) |
714
EXAMPLE 1 Converting from Cylindrical to Rectangular Coordinates
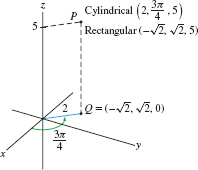
Find the rectangular coordinates of the point \(P\) with cylindrical coordinates \((r,\theta,z)=\big(2,\frac{3\pi}4,5\big)\).
Solution Converting to rectangular coordinates is straightforward (Figure 12.81): \begin{align*} x &= r\cos\theta = 2\cos\frac{3\pi}4 = 2\biggl(-\frac{\sqrt 2}2\biggr)=-\sqrt 2\\ y &= r\sin\theta = 2\sin\frac{3\pi}4 = 2\biggl(\frac{\sqrt 2}2\biggr)=\sqrt 2 \end{align*}
The \(z\)-coordinate is unchanged, so \((x,y,z)= (-\sqrt 2,\sqrt 2,5)\).
EXAMPLE 2 Converting from Rectangular to Cylindrical Coordinates
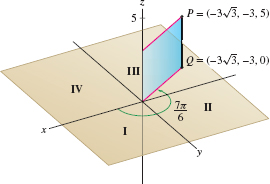
Find cylindrical coordinates for the point with rectangular coordinates \((x,y,z)=(-3\sqrt{3},-3,5)\).
Solution We have \({r= \sqrt{x^2+y^2} = \sqrt{(-3\sqrt 3)^2+(-3)^2} = 6}\). The angle \(\theta\) satisfies \[ \tan\theta = \frac{y}x = \frac{-3}{-3\sqrt 3} = \frac1{\sqrt 3} \quad\Rightarrow\quad \theta = \frac{\pi}6\quad\textrm{or}\quad \frac{7\pi}6 \]
The correct choice is \(\theta = \frac{7\pi}6\) because the projection \(Q = (-3\sqrt 3,-3,0)\) lies in the third quadrant (Figure 12.82). The cylindrical coordinates are \((r,\theta,z)=\big(6,\frac{7\pi}6,5\big)\).
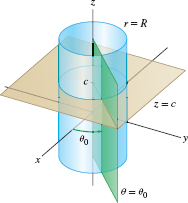
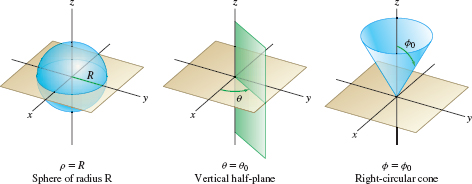
The level surfaces of a coordinate system are the surfaces obtained by setting one of the coordinates equal to a constant. In rectangular coordinates, the level surfaces are the planes \(x=x_0\), \(y=y_0\), and \(z = z_0\). In cylindrical coordinates, the level surfaces come in three types (Figure 12.83). The surface \(r=R\) is the cylinder of radius \(R\) consisting of all points located a distance \(R\) from the \(z\)-axis. The equation \(\theta=\theta_0\) defines the half-plane of all points that project onto the ray \(\theta=\theta_0\) in the \((x,y)\)-plane. Finally, \(z=c\) is the horizontal plane at height \(c\).
Note
Level Surfaces in Cylindrical Coordinates
| \(r = R\) | Cylinder of radius R with the z-axis as axis of symmetry |
| \(\theta = \theta_0\) | Half-plane through the z-axis making an angle \theta_0 with the xz-plane |
| \(z = c\) | Horizontal plane at height c |
EXAMPLE 3 Equations in Cylindrical Coordinates
Find an equation of the form \(z=f(r,\theta)\) for the surfaces
- (a) \({x^2+y^2+z^2=9}\)
- (b) \({x+y+z=1}\)
Solution We use the formulas \[ x^2+y^2=r^2,\qquad x=r\cos\theta,\qquad y=r\sin\theta \]
715
- (a) The equation \({x^2+y^2+z^2=9}\) becomes \({r^2+z^2=9}\), or \(z=\pm\sqrt{9-r^2}\). This is a sphere of radius 3.
- (b) The plane \(x+y+z=1\) becomes \[ z=1-x-y = 1-r\cos\theta-r\sin\theta\qquad \textrm{or}\qquad z = 1-r(\cos\theta+\sin\theta) \]
Spherical Coordinates
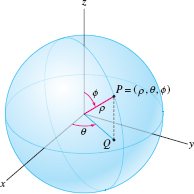
Spherical coordinates make use of the fact that a point \(P\) on a sphere of radius \(\rho\) is determined by two angular coordinates \(\theta\) and \(\phi\) (Figure 12.84):
- \(\theta\) is the polar angle of the projection \(Q\) of \(P\) onto the \(xy\)-plane.
- \(\phi\) is the angle of declination, which measures how much the ray through \(P\) declines from the vertical.
Thus \(P\) is determined by the triple \((\rho,\theta,\phi)\), which are called spherical coordinates.
Note
- The symbol \(\phi\) (usually pronounced “fee,” but sometimes pronounced “fie”) is the twenty-first letter of the Greek alphabet.
- We use \(\rho\) for the radial coordinate, although \(r\) is also used to denote distance from the origin in other contexts.
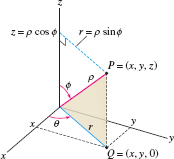
Suppose that \(P = (x,y,z)\) in rectangular coordinates. Since \(\rho\) is the distance from \(P\) to the origin, \( \rho = \sqrt{x^2+y^2+z^2} \)
On the other hand, we see in Figure 12.85 that \[ \tan\theta = \frac{y}x,\qquad \cos\phi = \frac{z}{\rho} \]
716
The radial coordinate \(r\) of \(Q=(x,y,0)\) is \(r = \rho\sin\phi\), and therefore, \[ x=r\cos\theta=\rho\cos\theta\sin\phi,\qquad y=r\sin\theta=\rho\sin\theta\sin\phi,\qquad z = \rho\cos\phi \]
| Spherical to rectangular | Rectangular to spherical |
| \({x=\rho\cos\theta\sin\phi}\) | \({\rho=\sqrt{x^2+y^2+z^2}}\) |
| \({y = \rho\sin\theta\sin\phi}\) | \({\tan\theta=\frac{y}{x}}\) |
| \({z = \rho\cos\phi}\) | \({\cos \phi =\frac{z}{\rho}}\) |
Note
Spherical Coordinates \begin{align*} \rho &= \textit{distance from origin}\\ \theta &= \textit{polar angle in the \(xy\)-plane}\\ \phi &= \textit{angle of declination from the vertical} \end{align*}
In some textbooks, \(\theta\) is referred to as the azimuthal angle and \(\phi\) as the polar angle.
EXAMPLE 4 From Spherical to Rectangular Coordinates
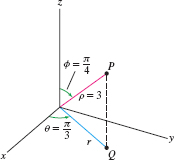
Find the rectangular coordinates of \(P = (\rho,\theta,\phi) = \big(3,\frac{\pi}3,\frac{\pi}4\big)\), and find the radial coordinate \(r\) of its projection \(Q\) onto the \(xy\)-plane.
Solution By the formulas above, \begin{eqnarray*} x&=& \rho\cos\theta\sin\phi = 3\cos\frac{\pi}3\sin\frac{\pi}4 = 3\left(\frac12\right)\frac{\sqrt 2}2 = \frac{3\sqrt 2}4\\ y&=& \rho\sin\theta\sin\phi = 3\sin\frac{\pi}3\sin\frac{\pi}4 = 3\left(\frac{\sqrt 3}2\right)\frac{\sqrt 2}2 = \frac{3\sqrt 6}4\\ z&=& \rho \cos\phi = 3\cos\frac{\pi}4 = 3\frac{\sqrt 2}2 = \frac{3\sqrt 2}2 \end{eqnarray*}
Now consider the projection \(Q =(x,y,0)=\left(\tfrac{3\sqrt 2}4,\tfrac{3\sqrt 6}4,0\right)\) (Figure 12.86). The radial coordinate \(r\) of \(Q\) satisfies \[ r^2 = x^2+y^2 = \left(\frac{3\sqrt 2}4\right)^2 +\left(\frac{3\sqrt 6}4\right)^2 = \frac92 \]
Therefore, \(r = 3/{\sqrt 2}\).
EXAMPLE 5 From Rectangular to Spherical Coordinates
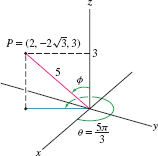
Find the spherical coordinates of the point \(P=(x,y,z)=(2,-2\sqrt3,3)\).
Solution The radial coordinate is \({\rho = \sqrt{2^2+(-2\sqrt3)^2+3^2}=\sqrt{25}=5}\). The angular coordinate \(\theta\) satisfies \[ \tan\theta =\frac{y}{x}=\frac{-2\sqrt3}2=-\sqrt3\quad \Rightarrow \quad \theta=\frac{2\pi}3 \textrm{or} \frac{5\pi}3 \]
Since the point \((x,y)= (2,-2\sqrt 3)\) lies in the fourth quadrant, the correct choice is \(\theta = \frac{5\pi}3\) (Figure 12.87). Finally, \(\cos\phi =\tfrac{z}{\rho}=\tfrac35\) and so \(\phi = \cos^{-1}\tfrac35 \approx 0.93\). Therefore, \(P\) has spherical coordinates \(\big(5,\frac{5\pi}3, 0.93\big)\).
Figure 12.88 shows the three types of level surfaces in spherical coordinates. Notice that if \(\phi \neq 0\), \(\frac{\pi}{2}\) or \(\pi\), then the level surface \(\phi=\phi_0\) is the right circular cone consisting of points \(P\) such that \(\overline{OP}\) makes an angle \(\phi_0\) with the \(z\)-axis. There are three exceptional cases: \(\phi = \frac{\pi}2\) defines the \(xy\)-plane, \(\phi = 0\) is the positive \(z\)-axis, and \(\phi =\pi\) is the negative \(z\)-axis.
717
EXAMPLE 6 Finding an Equation in Spherical Coordinates
Find an equation of the form \(\rho=f(\theta,\phi)\) for the following surfaces:
- (a) \({x^2+y^2+z^2=9}\)
- (b) \({z=x^2-y^2}\)
Solution
- (a) The equation \({x^2+y^2+z^2=9}\) defines the sphere of radius 3 centered at the origin. Since \({\rho^2=x^2+y^2+z^2}\), the equation in spherical coordinates is \(\rho=3\).
- (b) To convert \({z=x^2-y^2}\) to spherical coordinates, we substitute the formulas for \(x\), \(y\), and \(z\) in terms of \(\rho\), \(\theta\), and \(\phi\): \begin{eqnarray} \overbrace{\rho\cos\phi}^{z}&=&\overbrace{(\rho\cos\theta\sin\phi)^2}^{x^2}- \overbrace{(\rho\sin\theta\sin\phi)^2}^{y^2} \notag\\ \cos\phi&=& \rho\sin^2\phi(\cos^2\theta - \sin^2\theta)&&&(\textrm{divide by \(\rho\) and factor})\notag\\ \cos\phi &=& \rho\sin^2\phi\cos 2\theta &&&(\textrm{since \(\cos^2\theta - \sin^2\theta = \cos2\theta\)})\notag \end{eqnarray}
Solving for \(\rho\), we obtain \({ \rho = \frac{\cos\phi}{\sin^2\phi\cos2\theta}}\).
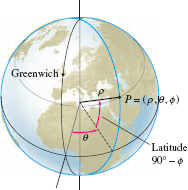
The angular coordinates \((\theta,\phi)\) on a sphere of fixed radius are closely related to the longitude-latitude system used to identify points on the surface of the earth (Figure 12.89). By convention, in this system we use degrees rather than radians.
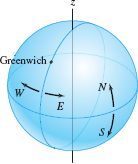
- A longitude is a half-circle stretching from the North to the South Pole (Figure 12.90). The axes are chosen so that \(\theta = 0\) passes through Greenwich, England (this longitude is called the prime meridian). We designate the longitude by an angle between 0 and \(180^\circ\) together with a label E or W, according to whether it lies to the east or west of the prime meridian.
- The set of points on the sphere satisfying \(\phi=\phi_0\) is a horizontal circle called a latitude. We measure latitudes from the equator and use the label N or S to specify the Northern or Southern Hemisphere. Thus, in the upper hemisphere \(0 \leq \phi_0 \leq 90^\circ\), a spherical coordinate \(\phi_0\) corresponds to the latitude \((90^\circ - \phi_0)\) N. In the lower hemisphere \(90^\circ \leq \phi_0 \leq 180^\circ\), \(\phi_0\) corresponds to the latitude \((\phi_0 - 90^\circ)\) S.
EXAMPLE 7 Spherical Coordinates via Longitude and Latitude
Find the angles \((\theta,\phi)\) for Nairobi (\(1.17^\circ\) S, \(36.48^\circ\) E) and Ottawa (\(45.27^\circ\) N, \(75.42^\circ\) W).
Solution For Nairobi, \(\theta = 36.48^\circ\) since the longitude lies to the east of Greenwich. Nairobi's latitude is south of the equator, so \(1.17 = \phi_0 - 90\) and \(\phi_0= 91.17^\circ\).
718
For Ottawa, we have \(\theta = 360-75.42 = 284.58^\circ\) because \(75.42^\circ\) W refers to 75.42 degrees in the negative \(\theta\) direction. Since the latitude of Ottawa is north of the equator, \(45.27 = 90- \phi_0\) and \(\phi_0 = 44.73^\circ\).
12.8.1 Summary
- Conversion from rectangular to cylindrical (Figure 12.91) and spherical
coordinates (Figure 12.92):
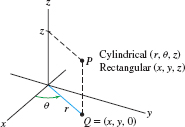 Figure 12.91: Cylindrical coordinates \((r,\theta,z)\).
Figure 12.91: Cylindrical coordinates \((r,\theta,z)\).Cylindrical Spherical \(r = \sqrt{x^2+y^2}\) \(\rho =\sqrt{x^2+y^2+z^2}\) \({\tan\theta = \frac{y}{x}}\) \({\tan\theta = \frac{y}{x}}\) \(z = z\) \({\cos\phi = \frac{z}{\rho}}\) The angles are chosen so that \[ 0\le \theta \lt 2\pi\quad\textrm{(cylindrical or spherical)},\qquad 0\le\phi\le\pi\quad \textrm{(spherical)} \]
- Conversion to rectangular coordinates:
 Figure 12.92: Spherical coordinates \((\rho,\theta,\phi)\).
Figure 12.92: Spherical coordinates \((\rho,\theta,\phi)\).Cylindrical \((r,\theta,z)\) Spherical \((\rho,\theta,\phi)\) \(x = r\cos\theta\) \(x=\rho\cos\theta\sin\phi\) \(y=r\sin\theta\) \(y=\rho\sin\theta\sin\phi\) \(z = z\) \(z = \rho\cos\phi\) - Level surfaces:
Cylindrical Spherical \(r=R\): Cylinder of radius \(R\) \(\rho=R\): Sphere of radius \(R\) \(\theta =\theta_0\):Vertical half-plane \(\theta =\theta_0\):Vertical half-plane \(z = c\):Horizontal plane \(\phi = \phi_0\):Right-circular cone