Calculus of Vector-Valued Functions

13.1 Vector-Valued Functions

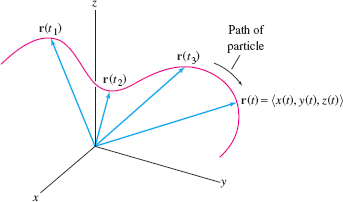
Consider a particle moving in \({\bf R}^3\) whose coordinates at time \(t\) are \((x(t), y(t), z(t))\). It is convenient to represent the particle’s path by the vector-valued function \[ \boxed{\bbox[#FAF8ED,5pt]{{\bf r}(t) = \langle x(t), y(t), z(t)\rangle = x(t){\bf i}+y(t){\bf j}+z(t){\bf k}}}\tag{1} \]

Think of \({\bf r}(t)\) as a moving vector that points from the origin to the position of the particle at time \(t\) (Figure 13.1).

Note

Functions \(f(x)\) (with real number values) are often called scalar-valued to distinguish them from vector-valued functions.

More generally, a vector-valued function is any function \({\bf r}(t)\) of the form in Eq. (1) whose domain \(D\) is a set of real numbers and whose range is a set of position vectors. The variable \(t\) is called a parameter, and the functions \(x(t), y(t), z(t)\) are called the components or coordinate functions. We usually take as domain the set of all values of \(t\) for which \({\bf r}(t)\) is defined—that is, all values of \(t\) that belong to the domains of all three coordinate functions \(x(t), y(t), z(t)\). For example, \begin{align*} {\bf r}(t) &= \langle t^2, e^t,4-7t\rangle,&\qquad &\textrm{domain \(D = {\bf R}\)}\\ {\bf r}(s) &= \langle \sqrt{s}, e^s,s^{-1}\rangle,&\qquad &\textrm{domain \(D =\{s\in {\bf R}: s>0\}\)} \end{align*}

Note

The parameter is often called \(t\) (for time), but we are free to use any other variable such as \(s\) or \(\theta\). It is best to avoid writing \({\bf r}(x)\) or \({\bf r}(y)\) to prevent confusion with the \(x\)- and \(y\)-components of \({\bf r}\).

724

The terminal point of a vector-valued function \({\bf r}(t)\) traces a path in \({\bf R}^3\) as \(t\) varies. We refer to \({\bf r}(t)\) either as a path or as a vector parametrization of a path. We shall assume throughout this chapter that the components of \({\bf r}(t)\) have continuous derivatives.

We have already studied special cases of vector parametrizations. In Chapter 12, we described lines in \({\bf R}^3\) using vector parametrizations. Recall that \[ {\bf r}(t) = \langle x_0,y_0,z_0\rangle + t{\bf v} = \langle x_0+ta,y_0+tb,z_0+tc\rangle \] parametrizes the line through \(P = (x_0,y_0,z_0)\) in the direction of the vector \({\bf v} = \langle a,b,c\rangle\).

In Chapter 11, we studied parametrized curves in the plane \({\bf R}^2\) in the form \[ c(t) = (x(t),y(t)) \]

Such a curve is described equally well by the vector-valued function \({\bf r}(t) = \langle x(t), y(t)\rangle\). The difference lies only in whether we visualize the path as traced by a “moving point” \(c(t)\) or a “moving vector” \({\bf r}(t)\). The vector form is used in this chapter because it leads most naturally to the definition of vector-valued derivatives.

It is important to distinguish between the path parametrized by \({\bf r}(t)\) and the underlying curve \(C\) traced by \({\bf r}(t)\). The curve \(C\) is the set of all points \((x(t),y(t),z(t))\) as \(t\) ranges over the domain of \({\bf r}(t)\). The path is a particular way of traversing the curve; it may traverse the curve several times, reverse direction, or move back and forth, etc.

EXAMPLE 1 The Path versus the Curve

Describe the path \[ {\bf r}(t) = \langle \cos t, \sin t, 1\rangle,\qquad -\infty < t < \infty \]

How are the path and the curve \(C\) traced by \({\bf r}(t)\) different?

Figure 13.2: Plot of \({\bf r}(t) =\langle \cos t, \sin t, 1\rangle\).

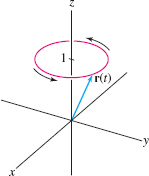
Solution As \(t\) varies from \(-\infty\) to \(\infty\), the endpoint of the vector \({\bf r}(t)\) moves around a unit circle at height \(z=1\) infinitely many times in the counterclockwise direction when viewed from above (Figure 13.2). The underlying curve \(C\) traced by \({\bf r}(t)\) is the circle itself.

A curve in \({\bf R}^3\) is also referred to as a space curve (as opposed to a curve in \({\bf R}^2\), which is called a plane curve). Space curves can be quite complicated and difficult to sketch by hand. The most effective way to visualize a space curve is to plot it from different viewpoints using a computer (Figure 13.3). As an aid to visualization, we plot a “thickened” curve as in Figure 13.3 and Figure 13.5, but keep in mind that space curves are one-dimensional and have no thickness.

Figure 13.3: The curve \({\bf r}(t)=\langle t\sin 2t\cos t,t\sin^2t,t\cos t\rangle\) for \(0\le t\le 4\pi\), seen from three different viewpoints.

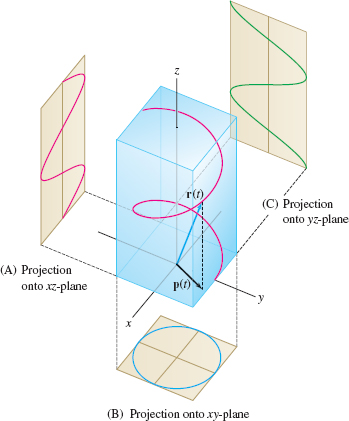
The projections onto the coordinate planes are another aid in visualizing space curves. The projection of a path \({\bf r}(t)=\langle x(t), y(t), z(t)\rangle\) onto the \(xy\)-plane is the path \({\bf p}(t) = \langle x(t), y(t), 0\rangle\) (Figure 13.4). Similarly, the projections onto the \(yz\)- and \(xz\)-planes are the paths \(\langle 0, y(t), z(t)\rangle\) and \(\langle x(t), 0, z(t)\rangle\), respectively.

725

EXAMPLE 2 Helix

Describe the curve traced by \({\bf r}(t) = \langle {-\sin t}, \cos t, t\rangle\) for \(t \geq 0\) in terms of its projections onto the coordinate planes.

Solution The projections are as follows (Figure 13.4):

\(xy\)-plane (set \(z=0\)): the path \({\bf p}(t)=\langle {-\sin t}, \cos t,0\rangle\), which describes a point moving counterclockwise around the unit circle starting at \({\bf p}(0) = (0,1,0)\).
\(xz\)-plane (set \(y=0\)): the path \(\langle {-\sin t}, 0, t\rangle\), which is a wave in the \(z\)-direction.
\(yz\)-plane (set \(x=0\)): the path \(\langle 0, \cos t, t\rangle\), which is a wave in the \(z\)-direction.

The function \({\bf r}(t)\) describes a point moving above the unit circle in the \(xy\)-plane while its height \(z=t\) increases linearly, resulting in the helix of Figure 13.4 .

Figure 13.4: Projections of the helix \({\bf r}(t) = \langle -\sin t, \cos t, t\rangle\).

Every curve can be parametrized in infinitely many ways (because there are infinitely many ways that a point can traverse a curve as a function of time). The next example describes two very different parametrizations of the same curve.

EXAMPLE 3 Parametrizing the Intersection of Surfaces

Parametrize the curve \(C\) obtained as the intersection of the surfaces \(x^2-y^2 = z-1\) and \(x^2+y^2=4\) (Figure 13.5).

Solution We have to express the coordinates \((x,y,z)\) of a point on the curve as functions of a parameter \(t\). Here are two ways of doing this.

First method: Solve the given equations for \(y\) and \(z\) in terms of \(x\). First, solve for \(y\): \[ x^2+y^2=4\quad\Rightarrow\quad y^2 = 4-x^2\quad\Rightarrow\quad y = \pm \sqrt{4-x^2} \]

The equation \(x^2-y^2=z-1\) can be written \(z=x^2-y^2+1\). Thus, we can substitute \(y^2 = 4-x^2\) to solve for \(z\): \[ z = x^2-y^2+1 = x^2 - (4-x^2)+1 = 2x^2-3 \]

726

Figure 13.5: Intersection of surfaces \(x^2-y^2=z-1\) and \(x^2+y^2=4\).

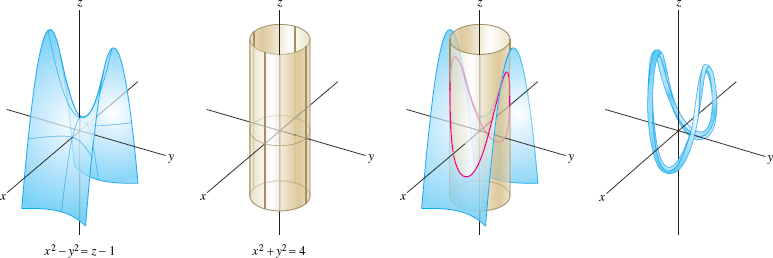
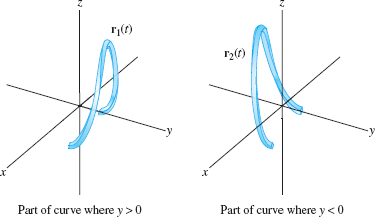
Now use \(t=x\) as the parameter. Then \(y = \pm\sqrt{4-t^2}\), \(z =2t^2-3\). The two signs of the square root correspond to the two halves of the curve where \(y>0\) and \(y<0\), as shown in Figure 13.6. Therefore, we need two vector-valued functions to parametrize the entire curve: \[ {\bf r}_1(t) = \langle t, \sqrt{4-t^2}, 2t^2-3\rangle,\quad {\bf r}_2(t) = \langle t, -\sqrt{4-t^2}, 2t^2-3\rangle,\qquad -2\le t \le 2 \]

Second method: Note that \(x^2+y^2=4\) has a trigonometric parametrization: \(x = 2\cos t\), \(y = 2\sin t\) for \(0 \le t < 2\pi\). The equation \(x^2-y^2 = z-1\) gives us \[ z = x^2-y^2+1 = 4\cos^2t-4\sin^2t+1=4\cos 2t +1 \]

Thus, we may parametrize the entire curve by a single vector-valued function: \[ {\bf r}(t) = \langle 2\cos t, 2\sin t, 4\cos 2t +1\rangle, \qquad \textrm{ \(0 \le t < 2\pi\)} \]

Figure 13.6: Two halves of the curve of intersection in Example 3

EXAMPLE 4

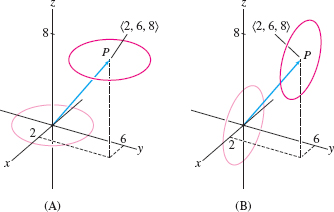
Parametrize the circle of radius 3 with center \(P=(2,6,8)\) located in a plane:

(a) Parallel to the \(xy\)-plane
(b) Parallel to the \(xz\)-plane

Solution (a) A circle of radius \(R\) in the \(xy\)-plane centered at the origin has parametrization \(\langle R\cos t, R\sin t\rangle\). To place the circle in a three-dimensional coordinate system, we use the parametrization \(\langle R\cos t,R\sin t,0\rangle\).

727

Thus, the circle of radius 3 centered at \((0,0,0)\) has parametrization \(\langle 3\cos t,3\sin t,0\rangle\). To move this circle in a parallel fashion so that its center lies at \(P=(2,6,8)\), we translate by the vector \(\langle 2,6,8\rangle\): \[ {\bf r}_1(t) = \langle 2,6,8\rangle + \langle 3\cos t,3\sin t,0\rangle = \langle 2+3\cos t, 6+3\sin t, 8\rangle \]

(b) The parametrization \(\langle 3\cos t,0, 3\sin t\rangle\) gives us a circle of radius 3 centered at the origin in the \(xz\)-plane. To move the circle in a parallel fashion so that its center lies at \((2,6,8)\), we translate by the vector \(\langle 2,6,8\rangle\): \[ {\bf r}_2(t) = \langle 2,6,8\rangle + \langle 3\cos t,0, 3\sin t\rangle = \langle 2+3\cos t , 6 , 8+3\sin t\rangle \]

These two circles are shown in Figure 13.7.

Figure 13.7: Horizontal and vertical circles of radius 3 and center \(P=(2,6,8)\) obtained by translation.

13.1.1 Summary

A vector-valued function is a function of the form \[ {\bf r}(t)=\langle x(t), y(t), z(t)\rangle = x(t){\bf i}+y(t){\bf j}+z(t){\bf k} \]
We often think of \(t\) as time and \({\bf r}(t)\) as a “moving vector” whose terminal point traces out a path as a function of time. We refer to \({\bf r}(t)\) as a vector parametrization of the path, or simply as a “ path.”
The underlying curve \(C\) traced by \({\bf r}(t)\) is the set of all points \((x(t),y(t),z(t))\) in \({\bf R}^3\) for \(t\) in the domain of \({\bf r}(t)\). A curve in \({\bf R}^3\) is also called a space curve.
Every curve \(C\) can be parametrized in infinitely many ways.
The projection of \({\bf r}(t)\) onto the \(xy\)-plane is the curve traced by \(\langle x(t), y(t),0\rangle\). The projection onto the \(xz\)-plane is \(\langle x(t),0, z(t)\rangle\), and the projection onto the \(yz\)-plane is \(\langle 0,y(t), z(t)\rangle\).