13.2 Calculus of Vector-Valued Functions
In this section, we extend differentiation and integration to vector-valued functions. This is straightforward because the techniques of single-variable calculus carry over with little change. What is new and important, however, is the geometric interpretation of the derivative as a tangent vector. We describe this later in the section.
The first step is to define limits of vector-valued functions.
DEFINITION Limit of a Vector-Valued Function
A vector-valued function \({\bf r}(t)\) approaches the limit \({\bf u}\) (a vector) as \(t\) approaches \(t_0\) if \(\displaystyle{\lim_{t\to t_0}\|{{\bf r}(t)-{\bf u}}\|=0}\). In this case, we write \[ \lim_{t\to t_0}{\bf r}(t) = {\bf u} \]
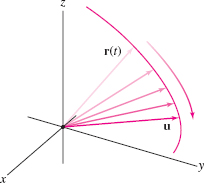
We can visualize the limit of a vector-valued function as a vector \({\bf r}(t)\) “moving” toward the limit vector \({\bf u}\) (Figure 13.8). According to the next theorem, vector limits may be computed componentwise.
THEOREM 1 Vector-Valued Limits Are Computed Componentwise
\({\bf r}(t)=\langle x(t), y(t), z(t)\rangle\) approaches a limit as \(t\to t_0\) if and only if each component approaches a limit, and in this case, \[ \lim_{t\to t_0}{\bf r}(t) = \langle \lim_{t\to t_0}x(t), \lim_{t\to t_0}y(t), \lim_{t\to t_0}z(t)\rangle\tag{1} \]
Proof
Let \({\bf u} = \langle a,b,c\rangle\) and consider the square of the length \[ \|{{\bf r}(t)-{\bf u}}\|^2 = (x(t)-a)^2+(y(t)-b)^2+(z(t)-c)^2\tag{2} \]
The term on the left approaches zero if and only if each term on the right approaches zero (because these terms are nonnegative). It follows that \(\|{{\bf r}(t)-{\bf u}}\|\) approaches zero if and only if \(|x(t)-a|\), \(|y(t)-b|\), and \(|z(t)-c|\) tend to zero. Therefore, \({\bf r}(t)\) approaches a limit \({\bf u}\) as \(t\to t_0\) if and only if \(x(t)\), \(y(t)\), and \(z(t)\) converge to the components \(a\), \(b\), and \(c\).
Note
The Limit Laws of scalar functions remain valid in the vector-valued case. They are verified by applying the Limit Laws to the components.
EXAMPLE 1
Calculate \(\displaystyle{\lim_{t\to 3}{\bf r}(t)}\), where \(\displaystyle{{\bf r}(t) = \langle t^2, 1-t, t^{-1}\rangle}\).
Solution By Theorem 1, \[ \lim_{t\to 3}{\bf r}(t) = \lim_{t\to 3}\langle t^2, 1-t, t^{-1}\rangle = \langle \lim_{t\to 3}t^2, \lim_{t\to 3}(1-t), \lim_{t\to 3} t^{-1}\rangle = \langle 9, -2, \frac13\rangle \]
732
Continuity of vector-valued functions is defined in the same way as in the scalar case. A vector-valued function \({\bf r}(t)=\langle x(t), y(t), z(t)\rangle\) is continuous at \(t_0\) if \[ \lim_{t\to t_0}\,{\bf r}(t) = {\bf r}(t_0) \]
By Theorem 1, \({\bf r}(t)\) is continuous at \(t_0\) if and only if the components \(x(t)\), \(y(t)\), \(z(t)\) are continuous at \(t_0\).
We define the derivative of \({\bf r}(t)\) as the limit of the difference quotient: \[ \boxed{\bbox[#FAF8ED,5pt]{{\bf r}'(t) = \dfrac{d}{dt}{\bf r}(t) = \lim_{h\to 0} \frac{{\bf r}(t+h) - {\bf r}(t)}{h}}}\tag{3} \]
In Leibniz notation, the derivative is written \(\displaystyle{d{\bf r}/{dt}\).
We say that \({\bf r}(t)\) is differentiable at \(t\) if the limit in Eq.(3) exists. Notice that the components of the difference quotient are difference quotients: \[ \lim_{h\to 0} \frac{{\bf r}(t+h) - {\bf r}(t)}{h} = \lim_{h\to 0} \langle \frac{x(t+h)-x(t)}h, \frac{y(t+h)-y(t)}h, \frac{z(t+h) -z(t)}h\rangle \] and by Theorem 1, \({\bf r}(t)\) is differentiable if and only if the components are differentiable. In this case, \({\bf r}'(t)\) is equal to the vector of derivatives \(\langle x'(t), y'(t), z'(t)\rangle\).
THEOREM 2 Vector-Valued Derivatives Are Computed Componentwise
A vector-valued function \({\bf r}(t)=\langle x(t), y(t), z(t)\rangle\) is differentiable if and only if each component is differentiable. In this case, \[ {\bf r}'(t) = \frac{d}{dt}{\bf r}(t) = \langle x'(t), y'(t), z'(t)\rangle \]
Note
By Theorems 1 and 2, vector-valued limits and derivatives are computed “componentwise,” so they are not more difficult to compute than ordinary limits and derivatives.
Here are some vector-valued derivatives, computed componentwise: \[ \frac{d}{dt} \langle t^2, t^3, \sin t\rangle = \langle 2t, 3t^2, \cos t\rangle,\qquad \frac{d}{dt} \langle \cos t, -1, e^{2t}\rangle = \langle -\sin t, 0, 2e^{2t}\rangle \] Higher-order derivatives are defined by repeated differentiation: \[ {\bf r}”(t)=\frac{d}{dt}\,{\bf r}'(t),\quad {\bf r}”'(t)=\frac{d}{dt}\, {\bf r}”(t),\quad \dots \]
EXAMPLE 2
Calculate \({\bf r}''(3)\), where \({\bf r}(t)=\langle \ln t, t, t^2\rangle\).
Solution We perform the differentiation componentwise: \begin{align*} {\bf r}'(t) =\frac{d}{dt}\,\langle \ln t, t, t^2\rangle =\langle t^{-1},1,2t\rangle\\ {\bf r}”(t) =\frac{d}{dt}\,\langle t^{-1},1,2t\rangle =\langle -t^{-2},0,2\rangle \end{align*} Therefore, \({\bf r}''(3) =\langle -\frac19,0,2\rangle\).
The differentiation rules of single-variable calculus carry over to the vector setting.
733
Differentiation Rules
Assume that \({\bf r}(t)\), \({\bf r}_1(t)\), and \({\bf r}_2(t)\) are differentiable. Then
- Sum Rule: \(\displaystyle{({\bf r}_1(t)+{\bf r}_2(t))' = {\bf r}_1'(t)+{\bf r}_2'(t)}\)
- Constant Multiple Rule: For any constant \(c\), \(\displaystyle{(c\,{\bf r}(t))' = c\,{\bf r}'(t)}\).
- Product Rule: For any differentiable scalar-valued function \(f(t)\), \[ \frac{d}{dt} \bigl(f(t){\bf r}(t)\bigr) = f(t) {\bf r}'(t)+f'(t){\bf r}(t) \]
- Chain Rule: For any differentiable scalar-valued function \(g(t)\), \[ \frac{d}{dt} \,{\bf r}(g(t)) = g'(t){\bf r}'(g(t)) \]
Proof
Each rule is proved by applying the differentiation rules to the components. For example, to prove the Product Rule (we consider vector-valued functions in the plane, to keep the notation simple), we write \[ f(t){\bf r}(t) = f(t)\langle x(t), y(t)\rangle = \langle f(t)x(t), f(t)y(t)\rangle \] Now apply the Product Rule to each component: \begin{align*} \frac{d}{dt} f(t){\bf r}(t) &= \langle \frac{d}{dt}f(t)x(t), \frac{d}{dt}f(t)y(t)\rangle\\ &= \langle f'(t)x(t)+f(t)x'(t), f'(t)y(t) + f(t)y'(t)\rangle\\ &= \langle f'(t)x(t), f'(t)y(t)\rangle + \langle f(t)x'(t), f(t)y'(t)\rangle \\ &= f'(t)\langle x(t), y(t) \rangle + f(t)\langle x'(t), y'(t)\rangle = f'(t){\bf r}(t)+f(t){\bf r}'(t) \end{align*} The remaining proofs are left as exercises (Exercises 69–70).
EXAMPLE 3
Let \({\bf r}(t)=\langle t^2, 5t, 1\rangle\) and \(f(t)= e^{3t}\). Calculate:
- (a) \(\displaystyle{\frac{d}{dt} f(t){\bf r}(t)}\)
- (b) \(\displaystyle{\frac{d}{dt} {\bf r}(f(t))}\)
Solution We have \({\bf r}'(t)=\langle 2t, 5 , 0\rangle\) and \(f'(t)=3e^{3t}\).
- (a) By the Product Rule, \[\begin{align*} \frac{d}{dt} f(t){\bf r}(t) & = f(t){\bf r}'(t)+f'(t){\bf r}(t) = e^{3t}\langle 2t, 5,0 \rangle + 3e^{3t}\langle t^2 , 5t, 1\rangle\\ &= \langle (3t^2+2t)e^{3t}, (15t+5)e^{3t}, 3e^{3t} \rangle \end{align*}\]
- (b) By the Chain Rule, \begin{align*} \frac{d}{dt} {\bf r}(f(t)) &= f'(t){\bf r}'(f(t)) = 3e^{3t}{\bf r}'(e^{3t}) = 3e^{3t}\langle 2e^{3t}, 5 , 0\rangle = \langle 6e^{6t},15e^{3t} , 0\rangle \end{align*}
There are three different Product Rules for vector-valued functions. In addition to the rule for the product of a scalar function \(f(t)\) and a vector-valued function \({\bf r}(t)\) stated above, there are Product Rules for the dot and cross products. These rules are very important in applications, as we will see.
734
THEOREM 3 Product Rule for Dot and Cross Products
Assume that \({\bf r}_1(t)\) and \({\bf r}_2(t)\) are differentiable. Then \[ \begin{eqnarray} &&\textrm{Dot Products:}& \frac{d}{dt} \big({\bf r}_1(t)\cdot{\bf r}_2(t)\big) &=& {\bf r}_1(t)\cdot {\bf r}_2'(t)+{\bf r}_1'(t)\cdot {\bf r}_2(t)\tag{4}\\ &&\textrm{Cross Products:}& \frac{d}{dt} \big({\bf r}_1(t)\times {\bf r}_2(t)\big) &=& \bigl[{\bf r}_1(t)\times {\bf r}_2'(t)\bigr] + \bigl[{\bf r}_1'(t)\times {\bf r}_2(t)\bigr]\tag{5} \end{eqnarray} \]
Proof
We verify Eq. (4) for vector-valued functions in the plane. If \({\bf r}_1(t)=\langle x_1(t), y_1(t)\rangle \) and \({\bf r}_2(t)=\langle x_2(t), y_2(t)\rangle \), then \begin{align*} \frac{d}{dt} \bigl({\bf r}_1(t)\cdot{\bf r}_2(t)\bigr) &= \frac{d}{dt} \big(x_1(t)x_2(t)+y_1(t)y_2(t)\big)\\ &=x_1(t)x_2'(t)+x_1'(t)x_2(t)+y_1(t)y_2'(t)+y_1'(t)y_2(t)\\ &= \big(x_1(t)x_2'(t)+ y_1(t)y_2'(t) \big) + \big(x_1'(t)x_2(t)+y_1'(t)y_2(t) \big)\\ &= {\bf r}_1(t)\cdot{\bf r}_2'(t) + {\bf r}_1'(t)\cdot{\bf r}_2(t) \end{align*}
The proof of Eq. (5) is left as an exercise (Exercise 71).
CAUTION
Order is important in the Product Rule for cross products. The first term in Eq. (5) must be written as \[{\bf r}_1(t)\times {\bf r}_2'(t) \] not \({\bf r}_2'(t)\times {\bf r}_1(t)\). Similarly, the second term is \({\bf r}_1'(t)\times {\bf r}_2(t)\). Why is order not a concern for dot products?
In the next example and throughout this chapter, all vector-valued functions are assumed differentiable, unless otherwise stated.
EXAMPLE 4
Prove the formula \(\displaystyle{\frac{d}{dt} \bigl({\bf r}(t)\times{\bf r}'(t)\bigr) = {\bf r}(t)\times{\bf r}”(t)}\).
Solution By the Product Formula for cross products, \[ \frac{d}{dt} \bigl({\bf r}(t)\times{\bf r}'(t)\bigr) = {\bf r}(t)\times{\bf r}”(t) + \underbrace{{\bf r}'(t)\times{\bf r}'(t)}_{\textrm{Equals \({\bf 0}\)}} = {\bf r}(t)\times{\bf r}”(t) \]
Here, \({\bf r}'(t)\times{\bf r}'(t) ={\bf 0}\) because the cross product of a vector with itself is zero.
The Derivative as a Tangent Vector
The derivative vector \({\bf r}'(t_0)\) has an important geometric property: It points in the direction tangent to the path traced by \({\bf r}(t)\) at \(t=t_0\).
To understand why, consider the difference quotient, where \(\Delta {\bf r} = {\bf r}(t_0+ h)-{\bf r}(t_0)\) and \(\Delta t = h\) with \(h \neq 0\): \[ \frac{\Delta {\bf r}}{\Delta t} = \frac{{\bf r}(t_0+h)-{\bf r}(t_0)}{h}\tag{6} \]
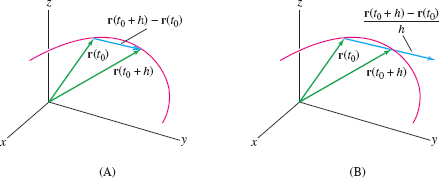
The vector \(\Delta {\bf r}\) points from the head of \({\bf r}(t_0)\) to the head of \({\bf r}(t_0+h)\) as in Figure 13.9. The difference quotient \(\Delta {\bf r}/\Delta t\) is a scalar multiple of \(\Delta {\bf r}\) and therefore points in the same direction [Figure 13.9].
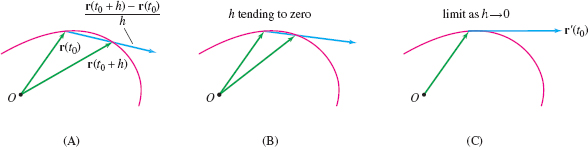
As \(h=\Delta t\) tends to zero, \(\Delta {\bf r}\) also tends to zero but the quotient \(\Delta {\bf r}/\Delta t\) approaches a vector \({\bf r}'(t_0)\), which, if nonzero, points in the direction tangent to the curve. Figure 13.10 illustrates the limiting process. We refer to \({\bf r}'(t_0)\) as the tangent vector or the velocity vector at \({\bf r}(t_0)\).
The tangent vector \(\displaystyle{{\bf r}'(t_0)}\) (if it is nonzero) is a direction vector for the tangent line to the curve. Therefore, the tangent line has vector parametrization: \[ \boxed{\bbox[#FAF8ED,5pt]{\textrm{Tangent line at \({\bf r}(t_0)\):}\qquad {\bf L}(t) = {\bf r}(t_0) + t\,{\bf r}'(t_0)}}\tag{7} \]
Note
Although it has been our convention to regard all vectors as based at the origin, the tangent vector \({\bf r}'(t)\) is an exception; we visualize it as a vector based at the terminal point of \({\bf r}(t)\). This makes sense because \({\bf r}'(t)\) then appears as a vector tangent to the curve ( Figure 13.10).
735
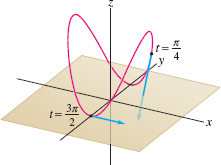
EXAMPLE 5 Plotting Tangent Vectors
![]() Plot \({\bf r}(t) = \langle \cos t, \sin t, 4\cos^2t\rangle\) together with its tangent vectors at \(t = \frac{\pi}4\) and \(\frac{3\pi}2\). Find a parametrization of the tangent line at \(t = \frac{\pi}4\).
Plot \({\bf r}(t) = \langle \cos t, \sin t, 4\cos^2t\rangle\) together with its tangent vectors at \(t = \frac{\pi}4\) and \(\frac{3\pi}2\). Find a parametrization of the tangent line at \(t = \frac{\pi}4\).
Solution The derivative is \(\displaystyle{ {\bf r}'(t) = \langle -\sin t, \cos t, -8\cos t\sin t\rangle}\), and thus the tangent vectors at \(t = \frac{\pi}4\) and \(\frac{3\pi}2\) are \[ {\bf r}'\left(\frac{\pi}4\right) = \langle -\frac {\sqrt 2}2, \frac{\sqrt 2}2, -4\rangle,\qquad {\bf r}'\left(\frac{3\pi}2\right) = \langle 1, 0, 0\rangle \]
Figure 13.11 shows a plot of \({\bf r}(t)\) with \({\bf r}'\big(\tfrac{\pi}4\big)\) based at \({\bf r}\big(\tfrac{\pi}4\big)\) and \({\bf r}'\big(\tfrac{3\pi}2\big)\) based at \({\bf r}\big(\tfrac{3\pi}2\big)\). At \(t=\frac{\pi}4\), \({\bf r}\big(\frac{\pi}4\big) = \langle \frac{\sqrt 2}2, \frac{\sqrt 2}2, 2 \rangle\) and thus the tangent line is parametrized by \[ {\bf L}(t) = {\bf r}\left(\frac{\pi}4\right) + t\,{\bf r}'\left(\frac{\pi}4\right) = \langle \frac{\sqrt 2}2, \frac{\sqrt 2}2, 2 \rangle + t \langle -\frac {\sqrt 2}2, \frac{\sqrt 2}2, -4\rangle \]
There are some important differences between vector- and scalar-valued derivatives. The tangent line to a plane curve \(y=f(x)\) is horizontal at \(x_0\) if \(f'(x_0)=0\). But in a vector parametrization, the tangent vector \({\bf r}'(t_0)=\langle x'(t_0), y'(t_0)\rangle\) is horizontal and nonzero if \(y'(t_0) = 0\) but \(x'(t_0)\ne 0\).
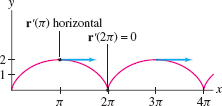
EXAMPLE 6 Horizontal Tangent Vectors on the Cycloid
The function \[ {\bf r}(t) = \langle t - \sin t, 1-\cos t\rangle \] traces a cycloid. Find the points where:
- (a) \({\bf r}'(t)\) is horizontal and nonzero.
- (b) \({\bf r}'(t)\) is the zero vector.
736
Solution The tangent vector is \({\bf r}'(t) = \langle 1 - \cos t, \sin t\rangle\). The \(y\)-component of \({\bf r}'(t)\) is zero if \(\sin t = 0\)—that is, if \(t = 0, \pi, 2\pi, \ldots.\) We have \begin{eqnarray*} {\bf r}(0) &=& \langle 0,0\rangle,& {\bf r}'(0) &=& \langle 1-\cos 0,\sin 0 \rangle = \langle 0,0\rangle\quad\textrm{(zero vector)}\\ {\bf r}( \pi ) &=& \langle \pi,2\rangle,& {\bf r}'(\pi) &=& \langle 1-\cos \pi,\sin \pi \rangle = \langle 2,0\rangle\quad\textrm{(horizontal)} \end{eqnarray*}
By periodicity, we conclude that \({\bf r}'(t)\) is nonzero and horizontal for \(t =\pi, 3\pi, 5\pi,\dots\) and \({\bf r}'(t)={\bf 0}\) for \(t=0, 2\pi, 4\pi,\dots\) (Figure 13.12).
CONCEPTUAL INSIGHT
The cycloid in Figure 13.12 has sharp points called cusps at points where \(x= 0, 2\pi, 4\pi,\dots\). If we represent the cycloid as the graph of a function \(y=f(x)\), then \(f'(x)\) does not exist at these points. By contrast, the vector derivative \({\bf r}'(t)=\langle 1-\cos t, \sin t\rangle\) exists for all \(t\), but \({\bf r}'(t)={\bf 0}\) at the cusps. In general, \({\bf r}'(t)\) is a direction vector for the tangent line whenever it exists, but we get no information about the tangent line (which may or may not exist) at points where \({\bf r}'(t)={\bf 0}\).
The next example establishes an important property of vector-valued functions that will be used in Sections 13.4–13.6.
EXAMPLE 7 Orthogonality of \({\bf r}\) and \({\bf r}'\) When \({\bf r}\) Has Constant Length
Prove that if \({\bf r}(t)\) has constant length, then \({\bf r}(t)\) is orthogonal to \({\bf r}'(t)\).
Solution By the Product Rule for Dot Products, \[ \frac{d}{dt} \|{{\bf r}(t)}\|^2 = \frac{d}{dt} \bigl({\bf r}(t)\cdot{\bf r}(t)\bigr) = {\bf r}(t)\cdot{\bf r}'(t)+{\bf r}'(t)\cdot{\bf r}(t) = 2{\bf r}(t)\cdot{\bf r}'(t) \]
This derivative is zero because \(\displaystyle{\|{{\bf r}(t)}}\|\) is constant. Therefore \displaystyle{{\bf r}(t)\cdot{\bf r}'(t)=0}, and \({\bf r}(t)\) is orthogonal to \({\bf r}'(t)\) [or \({\bf r}'(t)=\mathbf{0}\)].
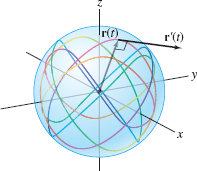
GRAPHICAL INSIGHT
The result of Example 7 has a geometric explanation. A vector parametrization \({\bf r}(t)\) consisting of vectors of constant length \(R\) traces a curve on the surface of a sphere of radius \(R\) with center at the origin (Figure 13.13). Thus \({\bf r}'(t)\) is tangent to this sphere. But any line that is tangent to a sphere at a point \(P\) is orthogonal to the radial vector through \(P\), and thus \({\bf r}(t)\) is orthogonal to \({\bf r}'(t)\).
Vector-Valued Integration
The integral of a vector-valued function can be defined in terms of Riemann sums as in Chapter 5. We will define it more simply via componentwise integration (the two definitions are equivalent). In other words, \[ \int_a^b {\bf r}(t)\, dt = \langle\, \int_a^b x(t)\,dt, \int_a^b y(t)\,dt, \int_a^b z(t)\,dt\rangle \]
The integral exists if each of the components \(x(t), y(t), z(t)\) is integrable. For example, \[ \int_0^{\pi} \langle 1, t,\sin t \rangle\, dt = \langle\, \int_0^{\pi}1\,dt, \int_0^{\pi} t\,dt,\int_0^{\pi} \sin t \,dt \rangle = \langle \pi , \frac12\pi^2 ,2 \rangle \]
Vector-valued integrals obey the same linearity rules as scalar-valued integrals (see Exercise 72).
An antiderivative of \({\bf r}(t)\) is a vector-valued function \({\bf R}(t)\) such that \({\bf R}'(t) = {\bf r}(t)\). In the single-variable case, two functions \(f_1(x)\) and \(f_2(x)\) with the same derivative differ by a constant. Similarly, two vector-valued functions with the same derivative differ by a constant vector (i.e., a vector that does not depend on \(t\)). This is proved by applying the scalar result to each component of \({\bf r}(t)\).
737
THEOREM 4
If \({\bf R}_1(t)\) and \({\bf R}_2(t)\) are differentiable and \({\bf R}_1'(t) = {\bf R}_2'(t)\), then \[ {\bf R}_1(t)={\bf R}_2(t)+c \] for some constant vector \(c\).
The general antiderivative of \({\bf r}(t)\) is written \[ \int {\bf r}(t)\,dt = {\bf R}(t)+c \] where \(c=\langle c_1, c_2, c_3\rangle\) is an arbitrary constant vector. For example, \[ \int \langle 1, t,\sin t \rangle\, dt =\langle t , \frac12t^2 , -\cos t \rangle +c= \langle t +c_1, \frac12t^2 +c_2, -\cos t +c_3\rangle \]
Fundamental Theorem of Calculus for Vector-Valued Functions
If \({\bf r}(t)\) is continuous on \([a,b]\), and \({\bf R}(t)\) is an antiderivative of \({\bf r}(t)\), then \[ \int_a^b {\bf r}(t)\, dt = {\bf R}(b)-{\bf R}(a) \]
EXAMPLE 8 Finding Position via Vector-Valued Differential Equations
The path of a particle satisfies \[ \frac{d{\bf r}}{dt} = \langle 1-6\sin 3t, \dfrac15t \rangle \] Find the particle’s location at \(t=4\) if \({\bf r}(0) = \langle 4,1\rangle\).
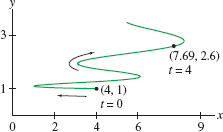
Solution The general solution is obtained by integration: \[ {\bf r}(t) = \int \langle 1-6\sin 3t, \dfrac15t \rangle\, dt = \langle t+2\cos 3t, \dfrac1{10}t^2\rangle + {\bf c} \]
The initial condition \({\bf r}(0)= \langle 4, 1\rangle\) gives us \[ {\bf r}(0) = \langle 2 , 0 \rangle + {\bf c} = \langle 4, 1\rangle \]
Therefore, \(\displaystyle{{\bf c} = \langle 2, 1\rangle}\) and (Figure 13.14) \[ {\bf r}(t) = \langle t+2\cos 3t, \dfrac1{10}t^2 \rangle+ \langle 2, 1\rangle= \langle t+2\cos 3t + 2, \dfrac1{10}t^2+1\rangle \]
The particle’s position at \(t=4\) is \[ {\bf r}(4)=\langle 4+2\cos 12 + 2, \dfrac1{10}(4^2)+1\rangle \approx \langle 7.69, 2.6\rangle \]
13.2.1 Summary
- Limits, differentiation, and integration of vector-valued functions are performed componentwise.
- Differentation rules:
- – Sum Rule: \(\displaystyle{({\bf r}_1(t)+{\bf r}_2(t))' = {\bf r}_1'(t)+{\bf r}_2'(t)}\)
- – Constant Multiple Rule: \(\displaystyle{ (c\,{\bf r}(t))' = c\,{\bf r}'(t)}\)
- – Chain Rule:
\(\displaystyle{\frac{d}{dt} \,{\bf r}(g(t)) = g'(t){\bf r}'(g(t))}\)
738
- Product Rules: \begin{eqnarray*} &&{\it Scalar times vector}:& \frac{d}{dt}\big(f(t){\bf r}(t)\big) &=& f(t){\bf r}'(t)+f'(t){\bf r}(t)\\ && {\it Dot product}:& \frac{d}{dt}\big({\bf r}_1(t)\cdot {\bf r}_2(t)\big) &=& {\bf r}_1(t)\cdot {\bf r}_2'(t)+{\bf r}_1'(t)\cdot {\bf r}_2(t)\\ && {\it Cross product}:& \frac{d}{dt}\big({\bf r}_1(t)\times {\bf r}_2(t)\big) &=& \bigl[{\bf r}_1(t)\times {\bf r}_2'(t)\bigr]+\bigl[{\bf r}_1'(t)\times {\bf r}_2(t)\bigr] \end{eqnarray*}
- The derivative \({\bf r}'(t_0)\) is called the tangent vector or velocity vector.
- If \({\bf r}'(t_0)\) is nonzero, then it points in the direction tangent to the curve at \({\bf r}(t_0)\). The tangent line has vector parametrization \[ {\bf L}(t) = {\bf r}(t_0) + t{\bf r}'(t_0) \]
- If \({\bf R}_1'(t)={\bf R}_2'(t)\), then \({\bf R}_1(t) = {\bf R}_2(t)+{\bf c}\) for some constant vector \({\bf c}\).
- The Fundamental Theorem for vector-valued functions: If \({\bf r}(t)\) is continuous and \({\bf R}(t)\) is an antiderivative of \({\bf r}(t)\), then \[ \int_a^b {\bf r}(t)\,dt = {\bf R}(b)-{\bf R}(a) \]