13.4 Curvature
Curvature is a measure of how much a curve bends. It is used to study geometric properties of curves and motion along curves, and has applications in diverse areas such as roller coaster design (Figure 13.19), optics,eye surgery (see Exercise 60), and biochemistry (Figure 13.20).

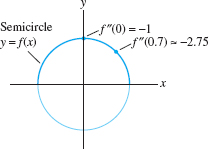
In Chapter 4, we used the second derivative \(f”(x)\) to measure the bending or concavity of the graph of \(y=f(x)\), so it might seem natural to take \(f”(x)\) as our definition of curvature. However, there are two reasons why this proposed definition will not work. First, \(f”(x)\) makes sense only for a graph \(y=f(x)\) in the plane, and our goal is to define curvature for curves in three-space. A more serious problem is that \(f”(x)\) does not truly capture the intrinsic curvature of a curve. A circle, for example, is symmetric, so its curvature ought to be the same at every point (Figure 13.21). But the upper semicircle is the graph of \(f(x)= (1-x^2)^{1/2}\) and the second derivative \(f”(x)=-(1-x^2)^{-3/2}\) does not have the same value at each point of the semicircle. We must look for a definition that depends only on the curve itself and not how it is oriented relative to the axes.
Consider a path with parametrization \({\bf r}(t) = \langle x(t), y(t),z(t) \rangle\). We assume that \({\bf r}'(t)\ne {\bf 0}\) for all \(t\) in the domain of \({\bf r}(t)\). A parametrization with this property is called regular. At every point \(P\) along the path there is a unit tangent vector \(\TT = \TT_P\) that points in the direction of motion of the parametrization. We write \(\TT(t)\) for the unit tangent vector at the terminal point of \({\bf r}(t)\): \[ \boxed{\bbox[#FAF8ED,5pt]{\textrm{Unit tangent vector} = \TT(t) = \frac{{\bf r}'(t)}{\|{{\bf r}'(t)}}\| }} \]
For example, if \({\bf r}(t) =\langle t,t^2,t^3\rangle\), then \({\bf r}'(t) = \langle 1,2t,3t^2\rangle\), and the unit tangent vector at \(P = (1,1,1)\), which is the terminal point of \({\bf r}(1) = \langle 1,1,1\rangle\), is \[ \TT_P = \frac{\langle 1, 2 , 3 \rangle}{\|{\langle 1, 2,3 \rangle}\|} = \frac{\langle 1, 2 , 3 \rangle}{\sqrt{ 1^2+ 2^2+3^2}} = \langle \frac1{\sqrt{14}}, \frac2{\sqrt{14}}, \frac3{\sqrt{14}}\rangle \]
747
If we choose another parametrization, say \({\bf r}_1(s)\), then we can also view \(\TT\) as function of \(s\): \(\TT(s)\) is the unit tangent vector at the terminal point of \({\bf r}_1(s)\).
Now imagine walking along a path and observing how the unit tangent vector \(\displaystyle{\TT}\) changes direction (Figure 13.22). A change in \(\displaystyle{\TT}\) indicates that the path is bending, and the more rapidly \(\displaystyle{\TT}\) changes, the more the path bends. Thus, \(\displaystyle{\left\|{\frac{\TT}t}\right\|}\) would seem to be a good measure of curvature. However, \(\displaystyle{\left\|{\frac{\TT}t}\right\|}\) depends on how fast you walk (when you walk faster, the unit tangent vector changes more quickly). Therefore, we assume that you walk at unit speed. In other words, curvature is the magnitude \(\displaystyle{\kappa(s) =\left\|{\frac{\TT}s}\right\|}\), where \(s\) is the parameter of an arc length parametrization. Recall that \({\bf r}(s)\) is an arc length parametrization if \(\|{\bf r}(s)\| =1\) for all \(s\).

DEFINITION Curvature
Let \({\bf r}(s)\) be an arc length parametrization and \(\TT\) the unit tangent vector. The curvature at \({\bf r}(s)\) is the quantity (denoted by a lowercase Greek letter “kappa”) \[ \boxed{\bbox[#FAF8ED,5pt]{\kappa(s) = \left\|\frac{\TT}s\right\|}} \tag{1} \]
Our first two examples illustrate curvature in the case of lines and circles.
EXAMPLE 1 A Line Has Zero Curvature
Compute the curvature at each point on the line \({\bf r}(t) = \langle x_0,y_0,z_0\rangle + t{\bf u}\), where \(\|{{\bf u}}\|=1\).
Solution First, we note that because \({\bf u}\) is a unit vector, \({\bf r}(t)\) is an arc length parametrization. Indeed, \({\bf r}'(t)={\bf u}\) and thus \(\|{{\bf r}'(t)}\|= \|{{\bf u}}\|=1\). Thus we have \(\TT(t) = {\bf r}'(t)/\|{\bf r}'(t)\| = {\bf r}'(t)\) and hence \(\TT'(t) = {\bf r}”(t)=\mathbf{0}\) (because \({\bf r}'(t) = {\bf u}\) is constant). As expected, the curvature is zero at all points on a line: \[ \kappa(t) = \|{\frac{\TT}t}\| = \|{{\bf r}\|(t)} = 0 \]
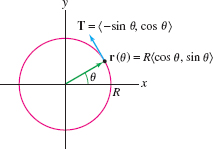
EXAMPLE 2 The Curvature of a Circle of Radius \(R\) Is \(1/R\)
Compute the curvature of a circle of radius \(R\).
Solution Assume the circle is centered at the origin, so that it has parametrization \({\bf r}(\theta)= \langle R\cos\theta, R\sin\theta\rangle\) (Figure 13.23). This is not an arc length parametrization if \(R \ne 1\). To find an arc length parametrization, we compute the arc length function: \[ s(\theta)= \int_0^{\theta}\|{{\bf r}'(u)}\|\,du = \int_0^{\theta}R\,du = R\theta \]
Thus \(s=R\theta\), and the inverse of the arc length function is \(\displaystyle{\theta =g(s) = {s}/R}\). In Section 13.3, we showed that \({\bf r}_1(s) = {\bf r}(g(s))\) is an arc length parametrization. In our case, we obtain \[ {\bf r}_1(s) = {\bf r}(g(s)) = {\bf r}\left(\frac{s}R\right) = \langle R\cos \frac{s}R , R\sin\frac{s}R\rangle \]
Note
Example 2 shows that a circle of large radius \(R\) has small curvature \(1/R\). This makes sense because your direction of motion changes slowly when you walk at unit speed along a circle of large radius.
748
The unit tangent vector and its derivative are \[ \begin{align*} \TT(s) &= \frac{{\bf r}_1}{s} = \frac{}{s}\langle R \cos \frac{s}{R}, R \sin \frac{s}{R} \rangle =\langle {-\sin \frac{s}R} ,\cos\frac{s}R\rangle\\ \frac{\TT}s &= -\frac1R\langle\cos\frac{s}R, \sin\frac{s}R\rangle \end{align*} \]
By definition of curvature, \[ \begin{align*} \kappa(s) &= \|{\frac{\TT}{s}}\| = \frac1R\|{\langle\cos\frac{s}R, \sin\frac{s}R\rangle}\| = \frac1R \end{align*} \]
This shows that the curvature is \(1/R\) at all points on the circle.
In practice, it is often impossible to find an arc length parametrization explicitly. Fortunately, we can compute curvature using any regular parametrization \({\bf r}(t)\). To derive a formula, we need the following two results.
Reminder
To prove that \(\TT(t)\) and \(\TT'(t)\) are orthogonal, note that \(\TT(t)\) is a unit vector, so \(\TT(t)\cdot\TT(t)=1\). Differentiate using the Product Rule for Dot Products: \[ \frac{d}{dt} \TT(t)\cdot\TT(t) = 2\TT(t)\cdot\TT'(t)=0 \]
This shows that \displaystyle{\TT(t)\cdot\TT'(t)=0}
First is the fact that \(\TT(t)\) and \(\TT'(t)\) are orthogonal (see the marginal note). Second, arc length \(s\) is function \(s(t)\) of time \(t\), so the derivatives of \(\TT\) with respect to \(t\) and \(s\) are related by the Chain Rule. Denoting the derivative with respect to \(t\) by a prime, we have \[ \TT'(t) = \frac{\TT}{t} = \frac{\TT}{s}\frac{s}{t} = v(t)\frac{\TT}{s} \] where \(\displaystyle{v(t) = \frac{s}t = \|{{\bf r}'(t)}}\|\) is the speed of \({\bf r}(t)\). Since curvature is the magnitude \(\displaystyle{\left\|{\frac{\TT}{s}}\right\|}\), we obtain \[ \|{\TT'(t)}\| = v(t)\kappa(t)\tag{2} \]
THEOREM 1 Formula for Curvature
If \({\bf r}(t)\) is a regular parametrization, then the curvature at \({\bf r}(t)\) is \[ \kappa(t) = \frac{\|{{\bf r}'(t)\|\times {\bf r}”(t)}}{\|{{\bf r}'(t)}\|^3}\tag{3} \]
Note
To apply Eq.(3) to plane curves, replace \({\bf r}(t)=\langle x(t), y(t)\rangle\) by \({\bf r}(t)=\langle x(t), y(t),0\rangle\) and compute the cross product.
Proof
Since \(v(t)=\|{{\bf r}'(t)}\|\), we have \({\bf r}'(t) = v(t)\TT(t)\). By the Product Rule, \[ {\bf r}”(t) = v'(t)\TT(t) + v(t)\TT'(t) \]
Now compute the following cross product, using the fact that \(\TT(t)\times\TT(t)=\mathbf{0}\): \[ \begin{align} {\bf r}'(t)\times{\bf r}”(t) &= v(t)\TT(t)\times\big(v'(t)\TT(t)+v(t)\TT'(t)\big)\notag\\ &=v(t)^2\TT(t)\times\TT'(t)\tag{4} \end{align} \]
Because \(\displaystyle{\TT(t)\) and \(\displaystyle{\TT'(t)\) are orthogonal, \[ \|{\TT(t)\times \TT'(t)}\| = \|{\TT(t)}\|\,\, \|{\TT'(t)}\|\sin\frac{\pi}2 = \|{\TT'(t)}\| \]
REMINDER
By Theorem 1 in Section 12.4, \[ \|{{\bf v}\times{\bf w}}\|=\|{{\bf v}}\|\,\|{{\bf w}}\|\sin\theta \] where \(\theta\)is the angle between \({\bf v}\) and \({\bf w}\).
Eq.(4) yields \(\displaystyle{\|{{\bf r}'(t)\times{\bf r}''(t)\)\| = v(t)^2\|{\TT'(t)}\|}\). Using Eq.(2), we obtain \[ \|{{\bf r}'(t)\times{\bf r}''(t)}\| = v(t)^2\|{\TT'(t)}\| = v(t)^3\kappa(t) = \|{{\bf r}'(t)}\|^3\kappa(t) \]
This yields the desired formula.
749
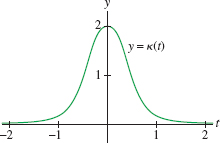
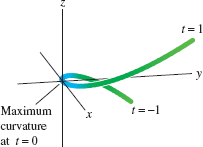
EXAMPLE 3 Twisted Cubic Curve
![]() Calculate the curvature \(\kappa(t)\) of the twisted cubic \({\bf r}(t)
= \langle t,t^2,t^3\rangle\). Then plot the graph of \(\kappa(t)\) and determine where
the curvature is largest.
Calculate the curvature \(\kappa(t)\) of the twisted cubic \({\bf r}(t)
= \langle t,t^2,t^3\rangle\). Then plot the graph of \(\kappa(t)\) and determine where
the curvature is largest.
Solution The derivatives are \[ {\bf r}'(t) = \langle 1,2t,3t^2\rangle ,\qquad {\bf r}”(t) = \langle 0,2,6t\rangle\\ \]
The parametrization is regular because \({\bf r}'(t)\ne{\bf 0}\) for all \(t\), so we may use Eq. (3): \begin{align*} {\bf r}'(t)\times {\bf r}”(t) &= \left| \begin{array}{ccc} {\bf i} & {\bf j} & {\bf k} \\ 1 & 2t & 3t^2 \\ 0 & 2 & 6t \\ \end{array} \right| = 6t^2{\bf i} -6t{\bf j}+2{\bf k} \\ \kappa(t) &= \frac{\|{{\bf r}'(t)\times {\bf r}”(t)}}\|{\|{{\bf r}'(t)}\|^3} = \frac{\sqrt{36t^4+36t^2+4}}{(1+4t^2+9t^4)^{3/2}} \end{align*}
The graph of \(\kappa(t)\) in Figure 13.24 shows that the curvature is largest at \(t = 0\). The curve \({\bf r}(t)\) is illustrated in Figure 13.25. The plot is colored by curvature, with large curvature represented in blue, small curvature in green.
In the second paragraph of this section, we pointed out that the curvature of a graph \(y=f(x)\) must involve more than just the second derivative \(f”(x)\). We now show that the curvature can be expressed in terms of both \(f”(x)\) and \(f'(x)\).
THEOREM 2 Curvature of a Graph in the Plane
The curvature at the point \((x,f(x))\) on the graph of \(y = f(x)\) is equal to \[ \boxed{\bbox[#FAF8ED,5pt]{\kappa(x) = \frac{|f”(x)|}{\big(1+f'(x)^2\big)^{3/2}}}}\tag{5} \]
Proof
The curve \(y=f(x)\) has parametrization \({\bf r}(x) = \langle x,f(x)\rangle\). Therefore, \({\bf r}'(x)=\langle 1,f'(x)\rangle\) and \({\bf r}”(x)=\langle 0,f”(x)\rangle\). To apply Theorem 1, we treat \({\bf r}'(x)\) and \({\bf r}”(x)\) as vectors in \({\bf R}^3\) with \(z\)-component equal to zero. Then \[ {\bf r}'(x)\times {\bf r}”(x) = \left| \begin{array}{ccc} {\bf i} & {\bf j} & {\bf k} \\ 1 & f'(x) & 0 \\ 0 & f”(x) & 0 \\ \end{array} \right| = f”(x) {\bf k} \]
Since \(\|{{\bf r}'(x)}\| = \bigl\|\langle 1, f'(x)\rangle\bigr\| = (1+f'(x)^2)^{1/2}\), Eq. (3) yields \[ \kappa(x) = \frac{\|{{\bf r}'(x)\times {\bf r}”(x)}}\|{\|{{\bf r}'(x)}\|^3} = \frac{|f”(x)|}{\big( 1+f'(x)^2\big)^{3/2}} \]
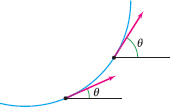
CONCEPTUAL INSIGHT
Curvature for plane curves has a geometric interpretation in terms of the angle of inclination, defined as the angle \(\theta\) between the tangent vector and the horizonal (Figure 13.26). The angle \(\theta\) changes as the curve bends, and we can show that the curvature \(\kappa\) is the rate of change of \(\theta\) as you walk along the curve at unit speed (see Exercise 61).
750
EXAMPLE 4
Compute the curvature of \(f(x) = x^3 - 3x^2 + 4\) at \(x = 0, 1, 2, 3\).
Solution We apply Eq. (5): \[ \begin{align*} f'(x)&=3x^2-6x=3x(x-2),\qquad f”(x)=6x-6\\ \kappa(x) &= \frac{|f”(x)|}{\big(1+f'(x)^2\big)^{3/2}} = \frac{|6x-6|}{\big(1+9x^2(x-2)^2\big)^{3/2}} \end{align*} \]
We obtain the following values: \[ \begin{eqnarray*} \kappa(0) &=& \frac{6}{(1+0)^{3/2}} = 6,& \quad\kappa(1) &=& \frac{0}{(1+9 )^{3/2}} = 0 \\ \kappa(2) &=& \frac{6}{(1+0)^{3/2}} = 6,& \quad\kappa(3) &=& \frac{12}{82^{3/2}} \approx 0.016 \end{eqnarray*} \]
Figure 13.27 shows that the graph bends more where the curvature is large.

Unit Normal Vector
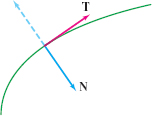
We noted above that \(\TT'(t)\) and \(\TT(t)\) are orthogonal. The unit vector in the direction of \(\TT'(t)\), assuming it is nonzero, is called the unit normal vector and is denoted \(\NN(t)\) or simply \(\NN\): \[ \boxed{\bbox[#FAF8ED,5pt]{ \textrm{Unit normal vector} =\NN(t) = \frac{\TT'(t)}{\|{\TT'(t)}\|}}}\tag{6} \]
Furthermore, \(\displaystyle{\norm{\TT'(t)} =v(t)\kappa(t)}\) by Eq. (2), so we have \[ \boxed{\bbox[#FAF8ED,5pt]{\TT'(t) = v(t)\kappa(t)\NN(t)}}\tag{7} \]
Intuitively, \(\NN\) points the direction in which the curve is turning (see Figure 13.29). This is particularly clear for a plane curve. In this case, there are two unit vectors orthogonal to \(\TT\) (Figure 13.28), and of these two, \(\NN\) is the vector that points to the “inside” of the curve.
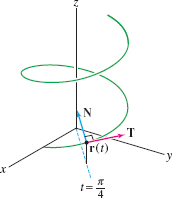
EXAMPLE 5 Unit Normal to a Helix
Find the unit normal vector at \(t=\frac{\pi}4\) to the helix \({\bf r}(t) = \langle \cos t, \sin t, t\rangle\).
Solution The tangent vector \({\bf r}'(t)= \langle -\sin t,\cos t, 1\rangle\) has length \(\sqrt{2}\), so \[ \begin{align*} \TT(t) &= \frac{{\bf r}'(t)}{\norm{{\bf r}'(t)}} = \frac1{\sqrt{2}}\langle -\sin t,\cos t,1\rangle \\ \TT'(t) &= \frac1{\sqrt{2}}\langle -\cos t, - \sin t,0\rangle \\ \NN(t) &= \frac{\TT'(t)}{\norm{\TT'(t)}} = \langle -\cos t,-\sin t, 0\rangle \end{align*} \]
Hence, \(\displaystyle{\NN\left(\frac{\pi}4\right)=\langle -\frac{\sqrt 2}2, -\frac{\sqrt 2}2, 0\rangle}\) (Figure #).
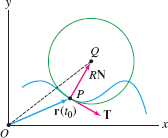
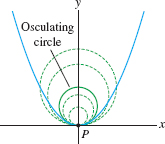
We conclude by describing another interpretation of curvature in terms of the osculating or “best-fitting circle” circle. Suppose that \(P\) is a point on a plane curve \(C\) where the curvature \(\kappa_P\) is nonzero. The osculating circle, denoted \(Osc_P\), is the circle of radius
751
\(R=1/\kappa_P\) through \(P\) whose center \(Q\) lies in the direction of the unit normal \(\NN\) (Figure 13.30). In other words, the center \(Q\) is determined by \[ \vc{OQ} = {\bf r}(t_0)+\kappa_P^{-1}\NN = {\bf r}(t_0) +R\NN\tag{8} \]
Among all circles tangent to \(C\) at \(P\), \(Osc_P\) “best fits” the curve (Figure 13.31; see also Exercise 71). We refer to \(R=1/\kappa_P\) as the radius of curvature at \(P\). The center \(Q\) of \(Osc_P\) is called the center of curvature at \(P\).
EXAMPLE 6
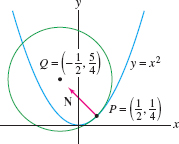
Parametrize the osculating circle to \(y=x^2\) at \(x=\frac12\).
Solution Let \(f(x) = x^2\). We use the parametrization \[ {\bf r}(x)=\langle x, f(x)\rangle = \big\langle x, x^2\big\rangle \] and proceed by the following steps.
Step 1. Find the radius
Apply Eq. (71) to \(f(x)=x^2\) to compute the curvature: \[ \kappa(x) = \frac{|f”(x)|}{\big(1+f'(x)^2\big)^{3/2}}= \frac{2}{\big(1+4x^2\big)^{3/2}},\qquad \kappa\left(\frac12\right)=\frac{2}{2^{3/2}} = \frac1{\sqrt{2}} \]
The osculating circle has radius \(R = 1/\kappa\big(\frac12\big) = \sqrt{2}\).
Step 2. Find \(\NN\) at \(t=\frac12\)
For a plane curve, there is an easy way to find \(\NN\) without computing \(\TT'\). The tangent vector is \({\bf r}'(x)=\langle 1,2x\rangle\), and we know that \(\langle 2x,-1\rangle\) is orthogonal to \({\bf r}'(x)\) (because their dot product is zero). Therefore, \(\NN(x)\) is the unit vector in one of the two directions \(\pm\langle 2x,-1\rangle\). Figure 13.32 shows that the unit normal vector points in the positive \(y\)-direction (the direction of bending). Therefore, \[ \NN(x) = \frac{\langle -2x,1\rangle}{\norm{\langle -2x,1\rangle}} = \frac{\langle -2x,1\rangle}{\sqrt{1+4x^2}},\qquad \NN\left(\frac12\right)=\frac1{\sqrt{2}}\langle -1,1\rangle \]
Step 3. Find the center \(Q\)
Apply Eq. (8) with \(t_0=\frac12\): \[ \vc{OQ} = {\bf r}\left(\frac12\right)+\kappa\left(\frac12\right)^{-1}\NN\left(\frac12\right) = \langle \frac12,\frac14\rangle + \sqrt 2\left(\frac{\langle -1,1\rangle}{\sqrt 2}\right) = \langle -\frac12,\frac54\rangle \]
Step 4. Parametrize the osculating circle
The osculating circle has radius \(R = \sqrt 2\), so it has parametrization \[ \boldc(t) = \underbrace{\langle -\frac12,\frac54\rangle}_{\textrm{Center}} + \sqrt{2}\langle \cos t, \sin t\rangle \]
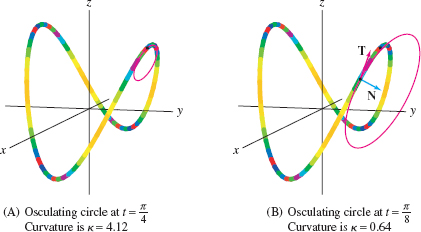
To define the osculating circle at a point \(P\) on a space curve \(C\), we must first specify the plane in which the circle lies. The osculating plane is the plane through \(P\) determined by the unit tangent \(\TT_P\) and the unit normal \(\NN_P\) at \(P\) (we assume that \(\TT'\ne 0\), so \(\NN\) is defined). Intuitively, the osculating plane is the plane that “most nearly” contains the curve \(C\) near \(P\) (see Figure 13.33). The osculating circle is the circle in the osculating plane through \(P\) of radius \(R=1/\kappa_P\) whose center is located in the normal direction \(N_P\) from \(P\). Equation (8) remains valid for space curves.
Note
If a curve \(C\) lies in a plane, then this plane is the osculating plane. For a general curve in three-space, the osculating plane varies from point to point.
752
13.4.1 Summary
- A parametrization \(r(t)\) is called regular if \({\bf r}'(t) \neq \mathbf{0}\) for all \(t\). If \(r(t)\) is regular, we define the unit tangent vector \(\TT(t) = \dfrac{{\bf r}'(t)}{\norm{{\bf r}'(t)}}\).
- Curvature is defined by \(\displaystyle{\kappa(s) = \left\Vert\frac{\TT}{s}\right\Vert}\), where \({\bf r}(s)\) is an arc length parametrization.
- In practice, we compute curvature using the following formula, which is valid for arbitrary regular parametrizations: \[ \kappa(t) = \frac{\norm{{\bf r}'(t)\times {\bf r}”(t)}}{\norm{{\bf r}'(t)}^3} \]
- The curvature at a point on a graph \(y=f(x)\) in the plane is \[ \kappa(x) = \frac{|f”(x)|}{\big(1+f'(x)^2\big)^{3/2}} \]
- If \(\norm{\TT'(t)}\ne 0\), we define the unit normal vector \(\displaystyle{\NN(t) = \frac{\TT'(t)}{\norm{\TT'(t)}}}\).
- \(\displaystyle{\TT'(t) = \kappa(t)v(t)\NN(t)}\)
- The osculating plane at a point \(P\) on a curve \(C\) is the plane through \(P\) determined by the vectors \(\TT_P\) and \(\NN_P\). It is defined only if the curvature \(\kappa_P\) at \(P\) is nonzero.
- The osculating circle \(Osc_P\) is the circle in the osculating plane through \(P\) of radius \(R=1/\kappa_P\) whose center \(Q\) lies in the normal direction \(\NN_P\): \[ \vc{OQ} = {\bf r}(t_0)+\kappa_P^{-1}\NN_P= {\bf r}(t_0) + R\NN_P \]
The center of \(Osc_P\) is called the center of curvature and \(R\) is called the radius of curvature.