13.5 Motion in Three-Space
In this section, we study the motion of a particle traveling along a path \({\bf r}(t)\). Recall that the velocity vector is the derivative \[ {\bf v}(t) = {\bf r}'(t) = \lim_{h\to 0}\frac{{\bf r}(t+h)-{\bf r}(t)}h \] As we have seen, \({\bf v}(t)\) points in the direction of motion (if it is nonzero), and its magnitude \(v(t)=\norm{{\bf v}(t)}\) is the particle’s speed. The acceleration vector is the second derivative \({\bf r}”(t)\), which we shall denote \(\bolda (t)\). In summary, \[ \boxed{\bbox[#FAF8ED,5pt]{{\bf v}(t) = {\bf r}'(t),\qquad v(t) = \norm{{\bf v}(t)},\qquad \bolda (t) = {\bf r}”(t)}}} \]

EXAMPLE 1
Calculate and plot the velocity and acceleration vectors at \(t = 1\) of \({\bf r}(t) = \langle \sin 2t, -\cos 2t,\sqrt{t+1} \rangle\).

Solution \[ \begin{align*}{2} {\bf v}(t) = {\bf r}'(t) &= \langle 2\cos 2t, 2\sin 2t, \frac12(t+1)^{-1/2} \rangle, &\qquad{\bf v}(1)&\approx\langle -0.83,0.84,0.35\rangle\\ \bolda(t) = {\bf r}”(t) & = \langle -4\sin 2t, 4\cos 2t, -\frac14(t+1)^{-3/2} \rangle, &\qquad\bolda(1)&\approx\langle -3.64,0.54,-0.089 \rangle \end{align*} \]
The speed at \(t=1\) is \[ \|{{\bf v}(1)}\|\approx\sqrt{(-0.83)^2+(0.84)^2+(0.35)^2} \approx 1.23 \]
If an object’s acceleration is given, we can solve for \({\bf v}(t)\) and \({\bf r}(t)\) by integrating twice: \[ \begin{align*} {\bf v}(t) &= \int\bolda(t)\, dt+{\bf v}_0\\ {\bf r}(t) &= \int_0^t{\bf v}(t)\, dt+{\bf r}_0 \end{align*} \] with \({\bf v}_0\) and \({\bf r}_0\) determined by initial conditions.
757
EXAMPLE 2
Find \({\bf r}(t)\) if \[ \bolda(t) =2{\bf i} +12t{\bf j},\qquad {\bf v}(0) = 7{\bf i}, \qquad {\bf r}(0)=2{\bf i}+9{\bf k} \]
Solution We have \[ \begin{align*} {\bf v}(t) &= \int \bolda(t)\,dt +{\bf v}_0= 2t{\bf i} +6t^2{\bf j} + {\bf v}_0 \intertext{The initial condition \({\bf v}(0) = {\bf v}_0 = 7{\bf i}\) gives us \({\bf v}(t)= 2t{\bf i} +6t^2 {\bf j} +7{\bf i}\). Then we have } {\bf r}(t) &= \int {\bf v}(t)\,dt +{\bf r}_0 = t^2{\bf i} +2t^3{\bf j} +7t{\bf i}+{\bf r}_0 \end{align*} \]
The initial condition \({\bf r}(0)={\bf r}_0=2{\bf i}+9{\bf k}\) yields \[ {\bf r}(t) = t^2{\bf i} +2t^3{\bf j} + 7t{\bf i}+(2{\bf i}+9{\bf k}) = (t^2+7t+2){\bf i}+2t^3{\bf j}+9{\bf k} \]
Newton’s Second Law of Motion is often stated in the scalar form \(F=ma\), but a more general statement is the vector law \({\bf F} = m\bolda\), where \({\bf F}\) is the net force vector acting on the object and \(\bolda\) is the acceleration vector. When the force varies from position to position, we write \({\bf F}({\bf r}(t))\) for the force acting on a particle with position vector \({\bf r}(t)\) at time \(t\). Then Newton’s Second Law reads \[ \boxed{\bbox[#FAF8ED,5pt]{ {\bf F}({\bf r}(t)) = m\bolda(t)\qquad \textrm{or}\qquad {\bf F}({\bf r}(t)) = m{\bf r}”(t)}}}\tag{1} \]
EXAMPLE 3
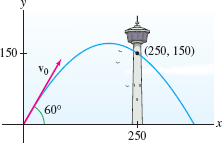
A bullet is fired from the ground at an angle of \(60^{\circ}\) above the horizontal. What initial speed \(v_0\) must the bullet have in order to hit a point 150 m high on a tower located 250 m away (ignoring air resistance)?
Solution Place the gun at the origin, and let \({\bf r}(t)\) be the position vector of the bullet (Figure 13.36).
Step 1. Use Newton’s Law.
Gravity exerts a downward force of magnitude \(mg\), where \(m\) is the mass of the bullet and \(g=9.8 \text{m/s}^2\). In vector form, \[ {\bf F} = \langle 0,-mg\rangle = m\langle 0, -g\rangle \]
Newton’s Second Law \({\bf F} = m{\bf r}”(t)\) yields \(m\langle 0, -g\rangle=m{\bf r}”(t)\) or \({\bf r}”(t)=\langle 0,- g \rangle\). We determine \({\bf r}(t)\) by integrating twice: \[ \begin{align*} {\bf r}'(t) &= \int_0^t {\bf r}”(u)\, du = \int_0^t \langle 0,-g\rangle\, du = \langle 0,- gt \rangle +{\bf v}_0\\ {\bf r}(t) &= \int_0^t {\bf r}'(u)\, du = \int_0^t \big(\langle 0,- gu \rangle +{\bf v}_0\big)\, du = \left\langle 0,- \frac12 gt^2 \right\rangle +t{\bf v}_0+{\bf r}_0 \end{align*} \]
758
Step 2. Use the initial conditions.
By our choice of coordinates, \({\bf r}_0 = \mathbf{0}\). The initial velocity \({\bf v}_0\) has unknown magnitude \(v_0\), but we know that it points in the direction of the unit vector \(\langle \cos 60^{\circ}, \sin 60^{\circ}\rangle\). Therefore, \[ \begin{align*} {\bf v}_0 &= v_0\langle \cos 60^{\circ}, \sin 60^{\circ}\rangle = v_0\langle \frac12, \frac{\sqrt{3}}2\rangle \\ {\bf r}(t) &= \left\langle 0,-\frac12gt^2\right\rangle +tv_0\langle \frac12, \frac{\sqrt{3}}2\rangle \]
Step 3. Solve for \(v_0\).
The bullet hits the point \(\langle 250, 150\rangle\) on the tower if there exists a time \(t\) such that \displaystyle{{\bf r}(t) = \langle 250, 150\rangle}; that is, \[ \left\langle 0,-\frac12gt^2\right\rangle +tv_0\langle \frac12, \frac{\sqrt{3}}2\rangle =\langle 250, 150\rangle \]
Equating components, we obtain \[ \frac12tv_0=250,\qquad - \frac12gt^2+ \frac{\sqrt{3}}2tv_0= 150 \]
The first equation yields \(\displaystyle{t = {500}/{v_0}}\). Now substitute in the second equation and solve, using \(g=9.8\): \[ \begin{align*} - 4.9\left(\frac{500}{v_0}\right)^2 &+\frac{\sqrt 3} 2\left(\frac{500}{v_0}\right)v_0 = 150 \\ \left(\frac{500}{v_0}\right)^2 &= \frac{250\sqrt 3 -150}{4.9}\\ \left(\frac{v_0}{500}\right)^2 &= \frac{4.9}{250\sqrt 3 -150} \approx 0.0173 \end{align*} \]
We obtain \displaystyle{v_0 \approx 500\sqrt{0.0173} \approx 66 \textrm{m/s}}.
In linear motion, acceleration is the rate at which an object is speeding up or slowing down. The acceleration is zero if the speed is constant. By contrast, in two or three dimensions, the acceleration can be nonzero even when the object’s speed is constant. This happens when \(v(t) = \norm{{\bf v}(t)}\) is constant but the direction of \({\bf v}(t)\) is changing. The simplest example is uniform circular motion, in which an object travels in a circular path at constant speed (Figure 13.37).

EXAMPLE 4 Uniform Circular Motion
Find \(\displaystyle{\bolda(t)}\) and \(\displaystyle{\norm{\bolda(t)}}\) for motion around a circle of radius \(R\) with constant speed \(v\).
Solution Assume that the particle follows the circular path \(\displaystyle{{\bf r}(t) = R\langle \cos \omega t, \sin \omega t\rangle}\) for some constant \(\omega\). Then the velocity and speed of the particle are \[ {\bf v}(t) = R\omega\langle -\sin \omega t, \cos \omega t\rangle,\qquad v = \norm{{\bf v}(t)} = R|\omega| \]
759
Thus \(|\omega| = v/R\), and accordingly, \[ \bolda(t)= {\bf v}'(t) = -R\omega^2\langle \cos \omega t,\sin \omega t\rangle,\qquad \norm{\bolda(t)} = R\omega^2 = R \left(\frac{v}R\right)^2 = \frac{v^2}R \]
The vector \(\bolda(t)\) is called the centripetal acceleration: It has length \(\displaystyle{ {v^2}/R}\) and points in toward the origin [because \(\bolda(t)\) is a negative multiple of the position vector \({\bf r}(t)\)], as in Figure 13.37.
Note
The constant \(\omega\) (lowercase Greek “omega”) is called the {\upshape angular speed} because the particle’s angle along the circle changes at a rate of \(\omega\) radians per unit time.
Understanding the Acceleration Vector
We have noted that \({\bf v}(t)\) can change in two ways: in magnitude and in direction. To understand how the acceleration vector \(\bolda(t)\) “encodes” both types of change, we decompose \(\bolda(t)\) into a sum of tangential and normal components.
Recall the definition of unit tangent and unit normal vectors: \[ \TT(t)=\frac{{\bf v}(t)}{\|{{\bf v}(t)}\|},\qquad \NN(t) = \frac{\TT'(t)}{\|{\TT'(t)}\|} \]
Thus, \({\bf v}(t) = v(t)\TT(t)\), where \(v(t) = \norm{{\bf v}(t)}\), so by the Product Rule, \[ \bolda (t) = \frac{{\bf v}}{t} = \frac{d}{dt}v(t)\TT(t)= v'(t)\TT(t)+v(t)\TT'(t) \]
Furthermore, \(\displaystyle{\TT'(t) = v(t)\kappa(t)\NN(t)}\) by Eq. (7) of Section 13.4, where \(\kappa(t)\) is the curvature. Thus we can write \[ \boxed{\bbox[#FAF8ED,5pt]{\bolda =a_{\TT} \TT +a_{\NN} \, \NN,\qquad a_{\TT} = v'(t),\quad a_{\NN} = \kappa(t)v(t)^2}}\tag{2} \]
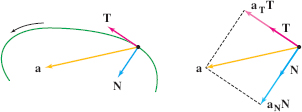
The coefficient \(a_{\TT}(t)\) is called the tangential component and \(a_{\NN}(t)\) the normal component of acceleration (Figure 13.38).
Note
When you make a left turn in an automobile at constant speed, your tangential acceleration is zero (because \(v'(t)=0\)) and you will not be pushed back against your seat. But the car seat (via friction) pushes you to the left toward the car door, causing you to accelerate in the normal direction. Due to inertia, you feel as if you are being pushed to the right toward the passenger’s seat. This force is proportional to \(\kappa v^2\), so a sharp turn (large \(\kappa\)) or high speed (large \(v\)) produces a strong normal force.
Note
The normal component \(a_\NN\) is often called the centripetal acceleration, especially in the case of circular motion where it is directed toward the center of the circle.
CONCEPTUAL INSIGHT
The tangential component \(a_\TT = v'(t)\) is the rate at which speed \(\displaystyle{v(t)}\) changes, whereas the normal component \(a_\NN=\kappa(t)v(t)^2\) describes the change in \({\bf v}\) due to a change in direction. These interpretations become clear once we consider the following extreme cases:
- A particle travels in a straight line. Then direction does not change [\(\kappa(t)=0\)] and \(\bolda(t) = v'(t)\TT\) is parallel to the direction of motion.
- A particle travels with constant speed along a curved path. Then \(v'(t)=0\) and the acceleration vector \(\bolda(t)=\kappa(t)v(t)^2\NN\) is normal to the direction of motion.
General motion combines both tangential and normal acceleration.
760
EXAMPLE 5
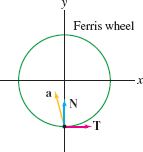
The Giant Ferris Wheel in Vienna has radius \(R=30\) m (Figure 13.39). Assume that at time \(t=t_0\), the wheel rotates counterclockwise with a speed of \(40 \text{m/min}\) and is slowing at a rate of \(15 \text{m/min}^2\). Find the acceleration vector \(\bolda\) for a person seated in a car at the lowest point of the wheel.
Solution At the bottom of the wheel, \(\TT = \langle 1,0 \rangle\) and \(\NN= \langle 0,1\rangle\). We are told that \(a_{\TT} = v' = -15\) at time \(t_0\). The curvature of the wheel is \(\kappa = 1/R=1/30\), so the normal component is \(a_{\NN} = \kappa v^2 = v^2/R= (40)^2/30 \approx 53.3 \(. Therefore (Figure 13.40), \[ \bolda \approx -15\TT+ 53.3\NN = \langle -15, 53.3 \rangle \text{m/min}^2 \]


The following theorem provides useful formulas for the tangential and normal components.
THEOREM 1 Tangential and Normal Components of Acceleration
In the decomposition \(\displaystyle{\bolda = a_\TT\TT+a_\NN\NN}\), we have \[ \boxed{a_{\TT} = \bolda\cdot\TT = \frac{\bolda\cdot{\bf v}}{\norm{{\bf v}}},\qquad a_\NN = \bolda\cdot\NN = \sqrt{\norm{\bolda}^2 - |a_\TT|^2}}\tag{3} \] and \[ \boxed{\bbox[#FAF8ED,5pt]{{a_{\TT}\TT = \left(\frac{\bolda\cdot{\bf v}}{{\bf v}\cdot{\bf v}}\right){\bf v},\qquad \bolda_{\NN}\NN=\bolda-a_{\TT} \TT = \bolda - \left(\frac{\bolda\cdot{\bf v}}{{\bf v}\cdot{\bf v}}\right){\bf v} }}}\tag{4} \]
Proof
We have \(\TT \cdot\TT =1\) and \(\NN\cdot\TT=0\). Thus \[ \begin{align*} \bolda\cdot\TT &= (a_\TT\TT+a_\NN\NN)\cdot\TT = a_{\TT}\\ \bolda\cdot\NN &= (a_\TT\TT+a_\NN\NN)\cdot\NN = a_{\NN} \end{align*} /] and since \displaystyle{\TT = \frac{{\bf v}}{\|{{\bf v}}\|}}, we have \[ a_\TT\TT = (\bolda\cdot\TT)\TT = \left(\frac{\bolda\cdot{\bf v}}{\|{{\bf v}}\|}\right)\frac{{\bf v}}{\|{{\bf v}}\|} = \left(\frac{\bolda\cdot{\bf v}}{{\bf v}\cdot{\bf v}}\right){\bf v} \] and \[ a_\NN\,\NN = \bolda - a_\TT\TT = \bolda - \left(\frac{\bolda\cdot{\bf v}}{\|{{\bf v}}\|}\right){\bf v} \]
Finally, the vectors \(a_\TT\TT\) and \(a_\NN\NN\) are the sides of a right triangle with hypotenuse \(\bolda\) as in Figure 13.38, so by the Pythagorean Theorem, \[ \|{\bolda}\|^2 = |a_\TT|^2+|a_\NN|^2\quad\Rightarrow\quad a_\NN =\sqrt{\|{\bolda}\|^2 - |a_\TT|^2}\]
Keep in mind that \(a_\NN\ge 0\) but \(a_\TT\) is positive or negative, depending on whether the object is speeding up or slowing down.
EXAMPLE 6
Decompose the acceleration vector \(\bolda\) of \({\bf r}(t)=\langle t^2,2t, \ln t\rangle\) into tangential and normal components at \(t = \frac12\) (Figure 13.41).
Solution First, we compute the tangential components \(\TT\) and \(a_\TT\). We have \[ {\bf v}(t)={\bf r}'(t) = \langle 2t, 2, t^{-1} \rangle,\qquad \bolda(t) = {\bf r}”(t) = \langle 2, 0, -t^{-2}\rangle \]
761
At \(t = \frac12\), \[ \begin{align*} {\bf v} &= {\bf r}'\left(\frac12\right)= \langle 2\left(\frac12\right), 2, \left(\frac12\right)^{-1} \rangle = \langle 1, 2, 2 \rangle\\ \bolda &= {\bf r}”\left(\frac12\right) = \langle 2, 0, -\left(\frac12\right)^{-2} \rangle= \langle 2, 0, -4\rangle \end{align*} \]
Thus \[ \TT = \frac{{\bf v}}{\norm{{\bf v}}} = \frac{\langle 1, 2, 2 \rangle}{\sqrt{1^2+2^2+2^2}} = \langle \frac13,\frac23,\frac23\rangle \] and by Eq. (3), \[ a_\TT = \bolda \cdot \TT = \langle2,0,-4\rangle \cdot \langle \frac{1}{3},\frac{2}{3},\frac{2}{3} \rangle = -2 \]
Next, we use Eq. (4): \[ a_\NN\NN= \bolda-a_\TT\TT = \langle 2, 0,-4\rangle - (-2) \langle \frac13,\frac23,\frac23 \rangle = \langle \frac83,\frac43,-\frac83 \rangle \]
This vector has length \[ a_\NN = \norm{a_\NN\NN} = \sqrt{\frac{64}9+ \frac{16}9 + \frac{64}9} = 4 \] and thus \[ \NN = \frac{a_\NN\NN}{a_\NN} = \frac{\langle \frac83,\frac43,-\frac83 \rangle}4 = \langle \frac23,\frac13,-\frac23 \rangle \]
Finally, we obtain the decomposition \[ \bolda = \langle 2, 0, -4\rangle = a_\TT \TT + a_\NN \NN = -2\TT + 4\NN \]
Note
Summary of steps in Example 6: \[ \begin{align*} \TT &= \frac{{\bf v}}{\norm{{\bf v}}}\\ a_\TT &= \bolda\cdot\TT\\ a_\NN\,\NN &= \bolda -a_\TT\TT\\ a_\NN &= \norm{a_\NN\,\NN}\\ \NN &= \frac{a_\NN\,\NN}{a_\NN} \end{align*} \]
EXAMPLE 7 Nonuniform Circular Motion
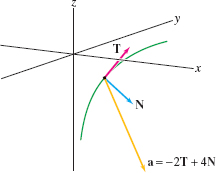
Figure # shows the acceleration vectors of three particles moving counterclockwise around a circle. In each case, state whether the particle’s speed \(v\) is increasing, decreasing, or momentarily constant.
REMINDER
- By Eq. (3), \(v'= a_\TT = \bolda\cdot \TT\)
- \displaystyle{{\bf v}\cdot{\bf w} = \norm{{\bf v}}\,\norm{{\bf w}}\cos\theta}
where \(\theta\) is the angle between \({\bf v}\) and \({\bf w}\).
Solution The rate of change of speed depends on the angle \(\theta\) between \(\bolda\) and \(\TT\): \[ v'= a_\TT = \bolda\cdot \TT = \norm{\bolda}\,\norm{\TT}\cos\theta = \norm{\bolda} \cos\theta \]
- In (A), \(\theta\) is obtuse so \(\cos\theta<0\) and \(v'<0\). The particle’s speed is decreasing.
- In (B), \(\theta=\frac{\pi}2\) so \(\cos \theta =0\) and \(v'=0\). The particle’s speed is momentarily constant.
- In (C), \(\theta\) is acute so \(\cos\theta>0\) and \(v'>0\). The particle’s speed is increasing.
762
EXAMPLE 8
Find the curvature \(\kappa\big(\frac12\big)\) for the path \({\bf r}(t)=\langle t^2,2t, \ln t\rangle\) in Example 6.
Solution By Eq. (2), the normal component is \[ a_\NN = \kappa v^2 \]
In Example 6 we showed that \(a_\NN = 4\) and \({\bf v}=\langle1,2,2\rangle\) at \(t=\frac12\). Therefore, \displaystyle{v^2 = {\bf v}\cdot{\bf v} = 9} and the curvature is \(\kappa\big(\frac12\big) = a_\NN/v^2 = \frac49\).
13.5.1 Summary
- For an object whose path is described by a vector-valued function \({\bf r}(t)\), \[ {\bf v}(t) = {\bf r}'(t),\qquad v(t) = \norm{{\bf v}(t)},\qquad \bolda (t) = {\bf r}”(t) \]
- The velocity vector \({\bf v}(t)\) points in the direction of motion. Its length \(v(t) = \norm{{\bf v}(t)}\) is the object’s speed.
- The acceleration vector \(\bolda\) is the sum of a tangential component (reflecting change in speed) and a normal component (reflecting change in direction): \[ \bolda(t) = a_\TT(t)\TT(t) + a_\NN(t)\NN(t) \]
| Unit tangent vector | \(\displaystyle{\TT(t) = \frac{{\bf v}(t)\arule}{\|{{\bf v}(t)}\|}}\) |
| Unit normal vector | \(\displaystyle{\NN(t) = \frac{\TT'(t)}{\norm{\TT'(t)}}}\) |
| Tangential component | \(\displaystyle{a_\TT = v'(t) = \bolda\cdot\TT = \frac{\bolda\cdot{\bf v}}{\norm{{\bf v}}}}\) |
| \(\displaystyle{a_\TT\TT =\left(\frac{\bolda\cdot{\bf v}}{{\bf v}\cdot{\bf v}}\right){\bf v}}\) | |
| Normal component | \(\displaystyle{a_\NN = \kappa(t)v(t)^2= \sqrt{\norm{\bolda}^2 - |\bolda_\TT|^2}}\) |
| \(\displaystyle{ a_\NN\,\NN = \bolda - a_\TT\TT = \bolda - \left(\frac{\bolda\cdot{\bf v}}{{\bf v}\cdot{\bf v}}\right){\bf v}\aabbrule}\) |