The partial derivative symbol \(\partial\) is a rounded “d.” The symbols \({\partial f}/{\partial x}\) and \({\partial f}/{\partial y}\) are read as follows: “dee-eff dee-ex” and “dee-eff dee-why.”

EXAMPLE 1

Compute the partial derivatives of \(f(x,y) = x^2y^5\).

Solution  \[ \begin{array}{rl} \frac{\partial f}{\partial x} &= \underbrace{\frac{\partial}{\partial x} \big(x^2y^5\big)= y^5\frac{\partial}{\partial x} \big(x^2\big)}_{\textrm{Treat }y^5\textrm{ as a constant}} = y^5(2x)=2xy^5 \\ \frac{\partial f}{\partial y} &= \underbrace{\frac{\partial}{\partial y} \big(x^2y^5\big)= x^2\frac{\partial}{\partial x} \big(y^5\big)}_{\textrm{Treat }x^2\textrm{ as a constant}} = x^2(5y^4)=5x^2y^4 \end{array} \]

GRAPHICAL INSIGHT

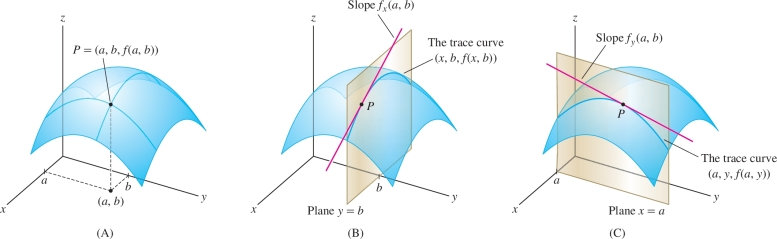
The partial derivatives at \(P = (a,b)\) are the slopes of the tangent lines to the vertical trace curves through the point \((a,b,f(a,b))\) in Figure 14.27. To compute \(f_x(a,b)\), we set \(y=b\) and differentiate in the \(x\)-direction. This gives us the slope of the tangent line to the trace curve in the plane \(y=b\) [Figure 14.27]. Similarly, \(f_y(a,b)\) is the slope of the trace curve in the vertical plane \(x=a\) [Figure 14.27].

EXAMPLE 2

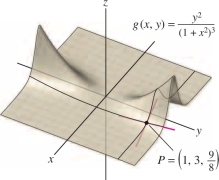
Calculate \(g_x(1,3)\) and \(g_y(1,3)\), where \(g(x,y)=\frac{y^2}{(1+x^2)^3}\).

Solution To calculate \(g_x\), treat \(y\) (and therefore \(y^2\)) as a constant: \[ \begin{array}{rl} g_x(x,y) &= \frac{\partial}{\partial x} \frac{y^2}{(1+x^2)^3} = y^2\frac{\partial}{\partial x} (1+x^2)^{-3}= \frac{-6xy^2}{(1+x^2)^4}\\ g_x(1,3)&= \frac{-6(1)3^2}{(1 + 1^2)^4} = -\frac{27}{8} \end{array} \] To calculate \(g_y\), treat \(x\) (and therefore \(1+x^2\)) as a constant: \begin{equation*} g_y(x,y) = \frac{\partial }{\partial y}\frac{y^2}{(1+x^2)^3} = \frac{1}{(1+x^2)^3}\frac{\partial }{\partial y}y^2 = \frac{2y}{(1+x^2)^3}\tag{1} \end{equation*} \[ g_y(1,3) = \frac{2(3)}{(1 + 1^2)^3} = \frac34 \]

These partial derivatives are the slopes of the trace curves through the point \(\big(1,3,\frac98\big)\) shown in Figure 14.28.

Figure 14.28: The slopes of the tangent lines to the trace curves are \(g_x(1,3)\) and \(g_y(1,3)\).

EXAMPLE 3 Chain Rule for Partial Derivatives

Compute \(\frac{\partial }{\partial x} \sin(x^2y^5)\).

Solution Write \(\sin(x^2y^5)=F(u)\), where \(F(u)=\sin u\) and \(u=x^2y^5\). Then we have \(\frac{d F}{d u} = \cos u\) and the Chain Rule give us \[ \underbrace{\frac{\partial }{\partial x} \sin(x^2y^5) = \frac{d F}{d u}\frac{\partial u}{\partial x}= \cos(x^2y^5)\frac{\partial }{\partial x}x^2y^5}_{\textrm{Chain Rule}} =2xy^5\cos(x^2y^5) \]

EXAMPLE 4 More Than Two Variables

Calculate \(f_z(0,0,1,1)\), where \[ f(x,y,z,w) = \frac{e^{xz+y}}{z^2+w} \]

Solution Use the Quotient Rule, treating \(x\), \(y\), and \(w\) as constants: \[ \begin{array}{rl} f_z(x,y,z,w) &= \frac{\partial}{\partial z}\left( \frac{e^{xz+y}}{z^2+w}\right) = \frac{(z^2+w)\frac{\partial}{\partial z} e^{xz+y}- e^{xz+y} \frac{\partial}{\partial z}(z^2+w)}{(z^2+w)^2} \\[6pt] &= \frac{(z^2+w)x e^{xz+y}- 2ze^{xz+y}}{(z^2+w)^2} = \frac{(z^2x+wx-2z)e^{xz+y}}{(z^2+w)^2}\\[6pt] f_z(0,0,1,1)&=\frac{-2e^0}{(1^2+1)^2}=-\frac12 \end{array} \]

In Example 4, the calculation \[ \frac{\partial}{\partial z} e^{xz+y}=xe^{xz+y} \] follows from the Chain Rule, just like \[ \frac{d }{d z} e^{az+b}=ae^{az+b} \]

EXAMPLE 5 Testing Microchips

A ball grid array (BGA) is a microchip joined to a circuit board by small solder balls of radius \(R\) mm separated by a distance \(L\) mm (Figure 14.29). Manufacturers test the reliability of BGAs by subjecting them to repeated cycles in which the temperature is varied from \(0^\circ\)C to \(100^\circ\)C over a 40-min period. According to one model, the average number \(N\) of cycles before the chip fails is \[ N = \left(\frac{2200R}{Ld} \right)^{1.9} \] where \(d\) is the difference between the coefficients of expansion of the chip and the board. Estimate the change \(\Delta N\) when \(R=0.12\), \(d = 10\), and \(L\) is increased from 0.4 to 0.42.

Figure 14.29: A BGA package. Temperature variations strain the BGA and may cause it to fail because the chip and board expand at different rates.

Solution We use the approximation \[ \Delta N \approx \frac{\partial N}{\partial L}\,\Delta L \] with \(\Delta L = 0.42-0.4 = 0.02\). Since \(R\) and \(d\) are constant, the partial derivative is \[ \frac{\partial N}{\partial L} = \frac{\partial}{\partial L} \left(\frac{2200R}{Ld} \right)^{1.9} = \left(\frac{2200R}{d} \right)^{1.9}\frac{\partial}{\partial L} L^{-1.9} = -1.9\left(\frac{2200R}{d} \right)^{1.9}L^{-2.9} \]

Now evaluate at \(L=0.4\), \(R=0.12\), and \(d=10\): \[ \frac{\partial N}{\partial L}\bigg|_{(L,R,d)=(0.4,0.12,10)} = -1.9\left(\frac{2200(0.12)}{10} \right)^{1.9}(0.4)^{-2.9}\approx -13{,}609 \]

The decrease in the average number of cycles before a chip fails is \[ \Delta N \approx \frac{\partial N}{\partial L}\Delta L =-13{,}609(0.02)\approx -272~\mathrm{cycles} \]

EXAMPLE 6 Estimating Partial Derivatives Using Contour Maps

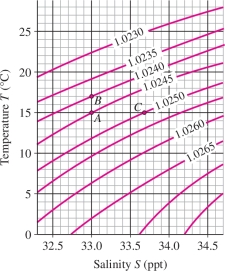
Seawater density \(\rho\) (\(\text{kg/m}^3\)) depends on salinity \(S\) (ppt) and the temperature \(T\) (\(^\circ\)C). Use Figure 14.30 to estimate \({\partial {\rho}}/{\partial T}\) and \({\partial {\rho}}/{\partial {S}}\) at \(A\).

Figure 14.30: Contour map of seawater density as a function of temperature and salinity.

Solution Point \(A\) has coordinates \((S,T)=(33,15)\) and lies on the level curve \(\rho=1.0245\). We estimate \({\partial {\rho}}/{\partial T}\) at \(A\) in two steps.

Step 1. Move vertically from \(A\).

Since \(T\) varies in the vertical direction, we move up vertically from point \(A\) to point \(B\) on the next higher level curve, where \(\rho = 1.0240\). Point \(B\) has coordinates \((S,T) = (33,17)\). Note that in moving from \(A\) to \(B\), we have kept \(S\) constant because both points have salinity \(S = 33\).

Step 2. Compute the difference quotient

\[ \begin{array}{rl} \Delta \rho &= 1.0240-1.0245=-0.0005\,\,\textrm{kg/m}^3\\ \Delta T &= 17 - 15 = 2^\circ \textrm{C} \end{array} \]

This gives us the approximation \[ \frac{\partial \rho}{\partial T}\bigg|_A \approx \frac{\Delta \rho}{\Delta T} = \frac{-0.0005}{2} = -0.00025~\text{kg-m}^{-3}/{}^\circ\text{C} \]

We estimate \({\partial {\rho}}/{\partial S}\) in a similar way, by moving to the right horizontally to point \(C\) with coordinates \((S,T) \approx (33.7,15)\), where \(\rho = 1.0250\): \[ \frac{\partial \rho}{\partial S}\bigg|_A \approx \frac{\Delta \rho}{\Delta S} =\frac{1.0250-1.0245}{33.7 - 33} = \frac{0.0005}{0.7} \approx 0.0007~\text{kg-m}^{-3}\text{/ppt} \]

EXAMPLE 7

Calculate the second-order partials of \(f(x,y)=x^3+y^2e^x\).

Solution First, we compute the first-order partial derivatives: \[ f_{x}(x,y) =\frac{\partial}{\partial x}\,(x^3+y^2e^x) = 3x^2+y^2e^x,\qquad f_{y}(x,y)= \frac{\partial}{\partial y}\,(x^3+y^2e^x) = 2ye^x \]

Then we can compute the second-order derivatives: \[ \begin{array}{llll} f_{xx}(x,y) &= \frac{\partial }{\partial x}f_x = \frac{\partial }{\partial x}(3x^2+y^2e^x)&\quad f_{yy}(x,y) &= \frac{\partial }{\partial y}f_y = \frac{\partial }{\partial y}2ye^x\\ & = 6x+y^2e^x,&\quad &= 2e^x\\ f_{xy}(x,y) &= \frac{\partial f_x}{\partial y} = \frac{\partial }{\partial y}(3x^2+y^2e^x) &\quad f_{yx}(x,y) &= \frac{\partial f_y}{\partial x} = \frac{\partial }{\partial x} 2ye^x\\ & =2ye^x,&\quad & =2ye^x \end{array} \]

Remember how the subscripts are used in partial derivatives. The notation \(f_{xyy}\) means “first differentiate with respect to \(x\) and then differentiate twice with respect to \(y\).”

EXAMPLE 8

Calculate \(f_{xyy}\) for \(f(x,y)=x^3+y^2e^x\).

Solution By the previous example, \(f_{xy}=2ye^x\). Therefore, \[ f_{xyy} = \frac{\partial }{\partial y}f_{xy} = \frac{\partial }{\partial y} 2ye^x = 2e^x \]

THEOREM 1 Clairaut’s Theorem: Equality of Mixed Partials

If \(f_{xy}\) and \(f_{yx}\) are both continuous functions on a disk \(D\), then \(f_{xy}(a,b) = f_{yx}(a,b)\) for all \((a,b)\in D\). In other words, \[ \boxed{\frac{\partial ^2f}{\partial x\, \partial y} = \frac{\partial ^2f}{\partial y\, \partial x}} \]

The hypothesis of Clairaut’s Theorem, that \(f_{xy}\) and \(f_{yx}\) are continuous, is almost always satisfied in practice, but see Exercise 84 for an example where the mixed partials are not equal.

EXAMPLE 9

Check that \( \frac{\partial^2W}{\partial U\partial T} =\frac{\partial^2W}{\partial T\partial U}\) for \(W = e^{U/T}\).

Solution We compute both derivatives and observe that they are equal: \[ \begin{array}{rclrcl} \frac{\partial W}{\partial T} &=&e^{U/T}\frac{\partial}{\partial T}\left(\frac{U}T\right) = -UT^{-2}e^{U/T}, & \frac{\partial W}{\partial U} &=& e^{U/T}\frac{\partial}{\partial U} \left(\frac{U}T\right) = T^{-1}e^{U/T} \\ \frac{\partial}{\partial U}\frac{\partial W}{\partial T} &=& -T^{-2}e^{U/T}-UT^{-3}e^{U/T}, & \frac{\partial}{\partial T}\frac{\partial W}{\partial U} &=& -T^{-2}e^{U/T}-UT^{-3}e^{U/T} \end{array} \]

EXAMPLE 10 Choosing the Order Wisely

Calculate the partial derivative \(g_{zzwx}\), where \(g(x,y,z,w) = x^3w^2z^2+\sin\left(\dfrac{xy}{z^2}\right)\).

Solution Let’s take advantage of the fact that the derivatives may be calculated in any order. If we differentiate with respect to \(w\) first, the second term disappears because it does not depend on \(w\): \[ g_w = \frac{\partial }{\partial w}\left(x^3w^2z^2+\sin\left(\frac{xy}{z^2}\right)\right) = 2x^3wz^2 \]

Next, differentiate twice with respect to \(z\) and once with respect to \(x\): \[ \begin{array}{rl} g_{wz} &= \frac{\partial }{\partial z}2x^3wz^2 = 4x^3wz\\ g_{wzz} &= \frac{\partial }{\partial z}4x^3wz = 4x^3w \\ g_{wzzx} &= \frac{\partial }{\partial x}4x^3w = 12x^2w \end{array} \]

We conclude that \(g_{zzwx} = g_{wzzx} = 12x^2w\).

EXAMPLE 11 The Heat Equation

Show that \(\smash{u(x,t)=\frac1{2\sqrt{\pi t}}e^{-(x^2/4t)}}\), defined for \(t>0\), satisfies the heat equation \begin{equation*} \frac{\partial u}{\partial t} = \frac{\partial^2u}{\partial x^2}\tag{2} \end{equation*}

Solution First, compute \(\smash{\frac{\partial ^2u}{\partial x^2}}\): \[ \begin{array}{llll} \frac{\partial u}{\partial x}&=\frac{\partial}{\partial x}\, \frac1{2\sqrt{\pi}}\,t^{-1/2}e^{-(x^2/4t)}& =&\;{-} \frac1{4\sqrt{\pi}}\,xt^{-3/2} e^{-(x^2/4t)}\\ \frac{\partial ^2u}{\partial x^2}&=\frac{\partial}{\partial x} \left(- \frac1{4\sqrt{\pi}}\, xt^{-3/2}e^{-(x^2/4t)}\right)\,& =&\;{-} \frac{1}{4\sqrt{\pi}}\,t^{-3/2}e^{-(x^2/4t)}+\frac1{8\sqrt{\pi}}\,x^2t^{-5/2}e^{-(x^2/4t)} \end{array} \]

Then compute \({\partial {u}}/{\partial {t}}\) and observe that it equals \({\partial {^2u}}/{\partial {x^2}}\) as required: \[ \frac{\partial u}{\partial t}=\frac{\partial}{\partial t}\left(\frac1{2\sqrt{\pi}}\,t^{-1/2}e^{-(x^2/4t)}\right) = -\frac1{4\sqrt{\pi}}\, t^{-3/2} e^{-(x^2/4t)}+\frac1{8\sqrt{\pi}}\,x^2t^{-5/2} e^{-(x^2/4t)} \]

HISTORICAL PERSPECTIVE

Joseph Fourier (1768–1830)

Adolf Fick (1829–1901)

The general heat equation, of which Eq. (2) is a special case, was first introduced in 1807 by French mathematician Jean Baptiste Joseph Fourier. As a young man, Fourier was unsure whether to enter the priesthood or pursue mathematics, but he must have been very ambitious. He wrote in a letter, “Yesterday was my 21st birthday, at that age Newton and Pascal had already acquired many claims to immortality.” In his twenties, Fourier got involved in the French Revolution and was imprisoned briefly in 1794 over an incident involving different factions. In 1798, he was summoned, along with more than 150 other scientists, to join Napoleon on his unsuccessful campaign in Egypt.

Fourier’s true impact, however, lay in his mathematical contributions. The heat equation is applied throughout the physical sciences and engineering, from the study of heat flow through the earth’s oceans and atmosphere to the use of heat probes to destroy tumors and treat heart disease.

Fourier also introduced a striking new technique—known as the Fourier transform—for solving his equation, based on the idea that a periodic function can be expressed as a (possibly infinite) sum of sines and cosines. Leading mathematicians of the day, including Lagrange and Laplace, initially raised objections because this technique was not easy to justify rigorously. Nevertheless, the Fourier transform turned out to be one of the most important mathematical discoveries of the nineteenth century. A Web search on the term “Fourier transform” reveals its vast range of modern applications.

In 1855, the German physiologist Adolf Fick showed that the heat equation describes not only heat conduction but also a wide range of diffusion processes, such as osmosis, ion transport at the cellular level, and the motion of pollutants through air or water. The heat equation thus became a basic tool in chemistry, molecular biology, and environmental science, where it is often called Fick’s Second Law.