14.6 The Chain Rule

The Chain Rule for Paths that we derived in the previous section can be extended to general composite functions. Suppose, for example, that \(x, y, z\) are differentiable functions of \(s\) and \(t\)—say \(x=x(s,t)\), \(y = y(s,t)\), and \(z=z(s,t)\). The composite \begin{equation*} f(x(s,t), y(s,t), z(s,t))\tag{1} \end{equation*} is then a function of \(s\) and \(t\). We refer to \(s\) and \(t\) as the independent variables.

826

EXAMPLE 1

Find the composite function where \(f(x,y,z) =xy+z\) and \(x=s^2\), \(y = st\), \(z = t^2\).

Solution The composite function is \[ f(x(s,t),y(s,t),z(s,t)) = xy+z = (s^2)(st)+t^2 = s^3t+t^2 \]

The Chain Rule expresses the derivatives of \(f\) with respect to the independent variables. For example, the partial derivatives of \(f (x(s,t), y(s,t), z(s,t) )\) are \begin{equation*} \frac{\partial f}{\partial s} = \frac{\partial f}{\partial x}\frac{\partial x}{\partial s} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial s} + \frac{\partial f}{\partial z} \frac{\partial z}{\partial s}\tag{2} \end{equation*} \begin{equation*} \frac{\partial f}{\partial t} = \frac{\partial f}{\partial x}\frac{\partial x}{\partial t} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial t} +\frac{\partial f}{\partial z} \frac{\partial z}{\partial t}\tag{3} \end{equation*}

To prove these formulas, we observe that \({\partial f}/{\partial s}\), when evaluated at a point \((s_0,t_0)\), is equal to the derivative with respect to the path \[ {\bf{c}}(s) = (x(s,t_0),y(s,t_0),z(s,t_0)) \]

In other words, we fix \(t=t_0\) and take the derivative with respect to \(s\): \[ \frac{\partial f}{\partial s}(s_0,t_0) = \frac{d }{d s}f({\bf{c}}(s))\bigg|_{s=s_0} \]

The tangent vector is \[ {\bf{c}}'(s)=\left\langle\frac{\partial x}{\partial s}(s,t_0),\frac{\partial y}{\partial s}(s,t_0),\frac{\partial z}{\partial s}(s,t_0)\right\rangle \]

Therefore, by the Chain Rule for Paths, \[ \frac{\partial f}{\partial s}\bigg|_{(s_0,t_0)} = \frac{d }{d s}f({\bf{c}}(s))\bigg|_{s=s_0} = \nabla f {\cdot} {\bf{c}}'(s_0) = \frac{\partial f}{\partial x}\frac{\partial x}{\partial s} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial s} + \frac{\partial f}{\partial z} \frac{\partial z}{\partial s} \]

The derivatives on the right are evaluated at \((s_0,t_0)\). This proves Eq. (2). A similar argument proves Eq. (3), as well as the general case of a function \(f(x_1,\dots,x_n)\), where the variables \(x_i\) depend on independent variables \(t_1,\dots,t_m\).

THEOREM 1 General Version of Chain Rule

Let \(f(x_1,\dots,x_n)\) be a differentiable function of \(n\) variables. Suppose that each of the variables \(x_1,\dots,x_n\) is a differentiable function of \(m\) independent variables \(t_1,\dots,t_m\). Then, for \(k=1,\dots,m\), \begin{equation*} \boxed{\frac{\partial f}{\partial t_k}=\frac{\partial f}{\partial x_1}\frac{\partial x_1}{\partial t_k}+\frac{\partial f}{\partial x_2}\frac{\partial x_2}{\partial t_k}+\cdots+\frac{\partial f}{\partial x_n}\frac{\partial x_n}{\partial t_k}}\tag{4} \end{equation*}

As an aid to remembering the Chain Rule, we will refer to \[ {\frac{\partial f}{\partial x_1}},\quad\ldots,\quad {\frac{\partial f}{\partial x_n}} \] as the primary derivatives. They are the components of the gradient \(\nabla f\). By Eq. (4), the derivative of \(f\) with respect to the independent variable \(t_k\) is equal to a sum of \(n\) terms: \[ j\textrm{th term:}\quad \frac{\partial f}{\partial x_j}\frac{\partial x_j}{\partial t_k}\quad \textrm{for }j = 1, 2,\dots, n \]

The term “primary derivative” is not standard. We use it in this section only, to clarify the structure of the Chain Rule.

827

Note that we can write Eq. (4) as a dot product: \begin{equation*} \boxed{\frac{\partial f}{\partial t_k} =\left\langle\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\dots,\frac{\partial f}{\partial x_n}\right\rangle {\cdot} \left\langle \frac{\partial x_1}{\partial t_k},\frac{\partial x_2}{\partial t_k},\dots,\frac{\partial x_n}{\partial t_k}\right\rangle}\tag{5} \end{equation*}

EXAMPLE 2 Using the Chain Rule

Let \(f(x,y,z) = xy+z\). Calculate \({\partial f}/{\partial s}\), where \[ x = s^2, \quad y = st,\quad z = t^2 \]

Solution

Step 1. Compute the primary derivatives

\[ \frac{\partial f}{\partial x} = y,\qquad \frac{\partial f}{\partial y} =x,\qquad \frac{\partial f}{\partial z} =1 \]

Step 2. Apply the Chain Rule.

\[ \begin{array}{rl} \frac{\partial f}{\partial s} = \frac{\partial f}{\partial x}\frac{\partial x}{\partial s} + \frac{\partial f}{\partial y}\frac{\partial y}{\partial s}+\frac{\partial f}{\partial z}\frac{\partial z}{\partial s} &= y \frac{\partial}{\partial s} (s^2) + x\frac{\partial}{\partial s} (st)+ \frac{\partial}{\partial s} (t^2)\\ &= (y)(2s) + (x)(t)+0 \\ &= 2sy + xt \end{array} \]

This expresses the derivative in terms of both sets of variables. If desired, we can substitute \(x = s^2\) and \(y = st\) to write the derivative in terms of \(s\) and \(t\): \[ \frac{\partial f}{\partial s} = 2ys+xt = 2(st)s+(s^2)t=3s^2t \]

To check this result, recall that in Example 1, we computed the composite function: \[ f(x(s,t),y(s,t),z(s,t)) = f(s^2, st, t^2) = s^3t+t^2 \]

From this we see directly that \({\partial f}/{\partial s}=3s^2t\), confirming our result.

EXAMPLE 3 Evaluating the Derivative

Let \(f(x,y) = e^{xy}\). Evaluate \({\partial f}/{\partial t}\) at \((s,t,u) = (2,3,-1)\), where \(x = st\), \(y = s - ut^2\).

Solution We can use either Eq. (4) or Eq. (5). We'll use the dot product form in Eq. (5). We have \[ \begin{array}{rl} \nabla f &= \left\langle\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right\rangle = \left\langle ye^{xy}, xe^{xy}\right\rangle,\qquad \left\langle \frac{\partial x}{\partial t}, \frac{\partial y}{\partial t}\right\rangle = \left\langle s, -2ut\right\rangle \end{array} \] and the Chain Rule gives us \[ \begin{array}{rl} \frac{\partial f}{\partial t} = \nabla f{\cdot} \left\langle \frac{\partial x}{\partial t}, \frac{\partial y}{\partial t}\right\rangle &= \left\langle ye^{xy}, xe^{xy}\right\rangle{\cdot} \left\langle s, -2ut\right\rangle\\ &= ye^{xy}(s) +xe^{xy}(-2ut)\\ &= (ys-2xut)e^{xy} \end{array} \]

To finish the problem, we do not have to rewrite \(\partial f/\partial t\) in terms of \(s,t,u\). For \((s,t,u) = (2,3,-1)\), we have \[ x=st = 2(3)=6,\qquad y=s-ut^2 = 2-(-1)(3^2) = 11 \]

With \((s,t,u) = (2,3,-1)\) and \((x,y) = (6, 11)\), we have \[ \frac{\partial f}{\partial t}\bigg|_{(2,3,-1)} = (ys-2xut)e^{xy}\bigg|_{(2,3,-1)} = \bigg((11)(2) - 2(6)(-1)(3)\bigg) e^{6(11)} = 58e^{66} \]

828

EXAMPLE 4 Polar Coordinates

Let \(f(x,y)\) be a function of two variables, and let \((r,\theta)\) be polar coordinates.

  • (a) Express \({\partial {f}}/{\partial {\theta}}\) in terms of \({\partial f}/{\partial x}\) and \({\partial f}/{\partial y}\).
  • (b) Evaluate \({\partial {f}}/{\partial {\theta}}\) at \((x,y)=(1,1)\) for \(f(x,y)=x^2y\).

Solution

  • (a) Since \(x=r\cos\theta\) and \(y=r\sin\theta\), \[ \frac{\partial x}{\partial \theta}=-r\sin\theta,\qquad \frac{\partial y}{\partial \theta}= r\cos\theta \] By the Chain Rule, \[ \frac{\partial f}{\partial \theta}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial \theta} + \frac{\partial f}{\partial y}\frac{\partial y}{\partial \theta} = -r\sin\theta\frac{\partial f}{\partial x}+r\cos\theta\frac{\partial f}{\partial y} \] Since \(x=r\cos\theta\) and \(y=r\sin\theta\), we can write \(\partial f/\partial\theta\) in terms of \(x\) and \(y\) alone: \begin{equation*} \frac{\partial f}{\partial \theta}=x\frac{\partial f}{\partial y} - y\frac{\partial f}{\partial x}\tag{6} \end{equation*}
  • (a) Apply Eq. (6) to \(f(x,y)=x^2y\): \[ \begin{array}{rl} &\frac{\partial f}{\partial \theta} = x\frac{\partial}{\partial y}\,(x^2y) - y\frac{\partial}{\partial x}(x^2y)=x^3-2xy^2\\ &\frac{\partial f}{\partial \theta}\bigg|_{(x,y)=(1,1)} = 1^3-2(1)(1^2)=-1 \end{array} \]

If you have studied quantum mechanics, you may recognize the right-hand side of Eq. (6) as the angular momentum operator (with respect to the \(z\)-axis).

Implicit Differentiation

In single-variable calculus, we used implicit differentiation to compute \({d y}/{d x}\) when \(y\) is defined implicitly as a function of \(x\) through an equation \(f(x,y)=0\). This method also works for functions of several variables. Suppose that \(z\) is defined implicitly by an equation \[ F(x,y,z)=0 \]

Thus \(z=z(x,y)\) is a function of \(x\) and \(y\). We may not be able to solve explicitly for \(z(x,y)\), but we can treat \(F(x,y,z)\) as a composite function with \(x\) and \(y\) as independent variables, and use the Chain Rule to differentiate with respect to \(x\): \[ \frac{\partial F}{\partial x}\frac{\partial x}{\partial x}+\frac{\partial F}{\partial y}\frac{\partial y}{\partial x}+\frac{\partial F}{\partial z}\frac{\partial z}{\partial x} = 0 \]

We have \({\partial x}/{\partial x} = 1\), and also \({\partial y}/{\partial x} = 0\) since \(y\) does not depend on \(x\). Thus \[ \frac{\partial F}{\partial x}+ \frac{\partial F}{\partial z}\frac{\partial z}{\partial x} = F_x+ F_z\frac{\partial z}{\partial x} =0 \]

If \(F_z\ne 0\), we may solve for \({\partial z}/{\partial x}\) (we compute \({\partial z}/{\partial y}\) similarly): \begin{equation*} \boxed{\frac{\partial z}{\partial x} = -\frac{F_x}{F_z},\qquad \frac{\partial z}{\partial y} = -\frac{F_y}{F_z} }\tag{7} \end{equation*}

829

EXAMPLE 5

Calculate \({\partial z}/{\partial x}\) and \({\partial z}/{\partial y}\) at \(P=(1,1,1)\), where \[ F(x,y,z) = x^2 + y^2 - 2z^2 + 12x - 8z - 4 = 0 \]

What is the graphical interpretation of these partial derivatives?

Solution We have \[ F_x = 2x+12,\qquad F_y = 2y, \qquad F_z = -4z-8 \] and hence, \[ \frac{\partial z}{\partial x} = -\frac{F_x}{F_z} = \frac{2x+12}{ 4z+8 }, \qquad \frac{\partial z}{\partial y} = -\frac{F_y}{F_z} = \frac{2y}{4z+8} \]

The derivatives at \(P=(1,1,1)\) are \[ \frac{\partial z}{\partial x}\bigg|_{(1,1,1)} = \frac{2(1)+12}{4(1)+8}=\frac{14}{ 12 }=\frac76,\quad\qquad\frac{\partial z}{\partial y}\bigg|_{(1,1,1)} = \frac{2(1)}{4(1)+8}=\frac{2}{12}=\frac16 \]

Figure 14.54 shows the surface \(F(x,y,z)=0\). The surface as a whole is not the graph of a function because it fails the Vertical Line Test. However, a small patch near \(P\) may be represented as a graph of a function \(z=f(x,y)\), and the partial derivatives \({\partial z}/{\partial x}\) and \({\partial z}/{\partial y}\) are equal to \(f_x\) and \(f_y\). Implicit differentiation has enabled us to compute these partial derivatives without finding \(f(x,y)\) explicitly.

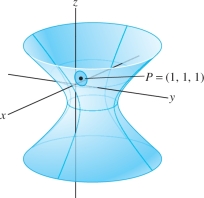
Figure 14.54: The surface \(x^2 + y^2 - 2z^2 + 12x - 8z - 4 = 0\). A small patch of the surface around \(P\) can be represented as the graph of a function of \(x\) and \(y\).

Assumptions Matter Implicit differentiation is based on the assumption that we can solve the equation \(F(x,y,z)=0\) for \(z\) in the form \(z=f(x,y)\). Otherwise, the partial derivatives \(\partial z/\partial x\) and \(\partial z/\partial y\) would have no meaning. The Implicit Function Theorem of advanced calculus guarantees that this can be done (at least near a point \(P\)) if \(F\) has continuous partial derivatives and \(F_z(P) \ne 0\). Why is this condition necessary? Recall that the gradient vector \(\nabla F_P = \left\langle F_x(P), F_y(P), F_z(P)\right\rangle\) is normal to the surface at \(P\), so \(F_z(P) = 0\) means that the tangent plane at \(P\) is vertical. To see what can go wrong, consider the cylinder (shown in Figure 14.55): \[ F(x,y,z)=x^2+y^2-1=0 \]

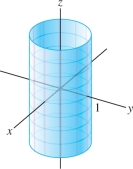
Figure 14.55: Graph of the cylinder \(x^2 + y^2 - 1 = 0\).

In this extreme case, \(F_z = 0\). The \(z\)-coordinate on the cylinder does not depend on \(x\) or \(y\), so it is impossible to represent the cylinder as a graph \(z=f(x,y)\) and the derivatives \(\partial z/\partial x\) and \(\partial z/\partial y\) do not exist.

14.6.1 Summary

830