14.8 Lagrange Multipliers: Optimizing with a Constraint
847
Some optimization problems involve finding the extreme values of a function \(f(x,y)\) subject to a constraint \(g(x,y) = 0\). Suppose that we want to find the point on the line \(2x+3y=6\) closest to the origin (Figure 14.70). The distance from \((x,y)\) to the origin is \(f(x,y)=\sqrt{x^2+y^2}\), so our problem is \[ \quad\textrm{Minimize}\,\,\,f(x,y)=\sqrt{x^2+y^2}\quad\textrm{subject to}\quad g(x,y) = 2x+3y-6 =0 \]
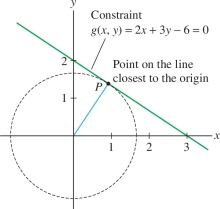
We are not seeking the minimum value of \(f(x,y)\) (which is \(0\)), but rather the minimum among all points \((x,y)\) that lie on the line.
The method of Lagrange multipliers is a general procedure for solving optimization problems with a constraint. Here is a description of the main idea.
GRAPHICAL INSIGHT
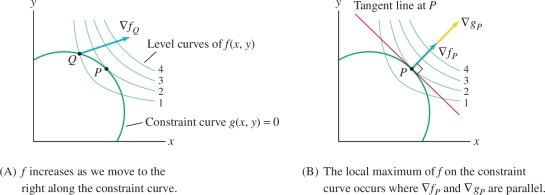
Imagine standing at point \(Q\) in Figure 14.71. We want to increase the value of \(f\) while remaining on the constraint curve. The gradient vector \(\nabla f_Q\) points in the direction of maximum increase, but we cannot move in the gradient direction because that would take us off the constraint curve. However, the gradient points to the right, and so we can still increase \(f\) somewhat by moving to the right along the constraint curve.
We keep moving to the right until we arrive at the point \(P\), where \(\nabla f_P\) is orthogonal to the constraint curve [Figure 14.71]. Once at \(P\), we cannot increase \(f\) further by moving either to the right or to the left along the constraint curve. Thus \(f(P)\) is a local maximum subject to the constraint.
Now, the vector \(\nabla g_P\) is also orthogonal to the constraint curve, so \(\nabla f_P\) and \(\nabla g_P\) must point in the same or opposite directions. In other words, \(\nabla f_P = \lambda \nabla g_P\) for some scalar \(\lambda\) (called a Lagrange multiplier). Graphically, this means that a local max subject to the constraint occurs at points \(P\) where the level curves of \(f\) and \(g\) are tangent.
THEOREM 1 Lagrange Multipliers
Assume that \(f(x,y)\) and \(g(x,y)\) are differentiable functions. If \(f(x,y)\) has a local minimum or a local maximum on the constraint curve \(g(x,y) = 0\) at \(P=(a,b)\), and if \(\nabla g_P\ne {\bf{0}}\), then there is a scalar \(\lambda\) such that \begin{equation*} \boxed{\nabla f_P = \lambda \nabla g_P}\tag{1} \end{equation*}
848
proof Let \({\bf{c}}(t)\) be a parametrization of the constraint curve \(g(x,y)=0\) near \(P\), chosen so that \({\bf{c}}(0)=P\) and \({\bf{c}}'(0)\ne \mathbf{0}\). Then \(f({\bf{c}}(0))=f(P)\), and by assumption, \(f({\bf{c}}(t))\) has a local min or max at \(t=0\). Thus, \(t=0\) is a critical point of \(f({\bf{c}}(t))\) and \[ \underbrace{\frac{d }{d t}f({\bf{c}}(t))\bigg|_{t=0} = \nabla f_P{\cdot} {\bf{c}}'(0)}_{\textrm{Chain Rule}} = 0 \]
This shows that \(\nabla f_P\) is orthogonal to the tangent vector \({\bf{c}}'(0)\) to the curve \(g(x,y)= 0\). The gradient \(\nabla g_P\) is also orthogonal to \({\bf{c}}'(0)\) (because \(\nabla g_P\) is orthogonal to the level curve \(g(x,y) = 0\) at \(P\)). We conclude that \(\nabla f_P\) and \(\nabla g_P\) are parallel, and hence \(\nabla f_P\) is a multiple of \(\nabla g_P\) as claimed.
In Theorem 1, the assumption \(\nabla g_P\ne {\bf{0}}\) guarantees (by the Implicit Function Theorem of advanced calculus) that we can parametrize the curve \(g(x,y)=0\) near \(P\) by a path \({\bf{c}}\) such that \({\bf{c}}(0) = P\) and \({\bf{c}}'(0) \neq {\bf{0}}\).
REMINDER
Eq. (1) states that if a local min or max of \(f(x,y)\) subject to a constraint \(g(x,y) = 0\) occurs at \(P = (a,b)\), then \[ \nabla f_P = \lambda \nabla g_P \] provided that \(\nabla g_P \ne \mathbf{0}\).
We refer to Eq. (1) as the Lagrange condition. When we write this condition in terms of components, we obtain the Lagrange equations: \[ \begin{array}{rl} f_x(a,b)&=\lambda g_x(a,b)\\ f_y(a,b)&=\lambda g_y(a,b) \end{array} \]
A point \(P=(a,b)\) satisfying these equations is called a critical point for the optimization problem with constraint and \(f(a,b)\) is called a critical value.
EXAMPLE 1
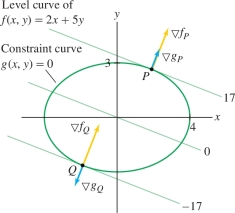
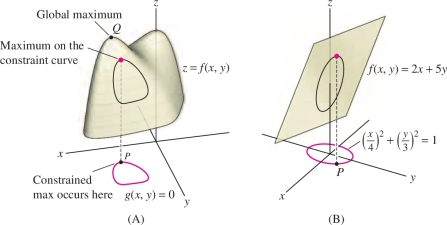
Find the extreme values of \(f(x,y) = 2x+5y\) on the ellipse \[ \left(\frac{x}4\right)^2+\left(\frac{y}3\right)^2= 1 \]
Solution
Step 1. Write out the Lagrange equations.
The constraint curve is \(g(x,y)=0\), where \(g(x,y) =\left({x}/4\right)^2+\left({y}/3\right)^2-1\). We have \[ \nabla f=\left\langle 2, 5\right\rangle,\qquad \nabla g = \left\langle \frac{x}8, \frac{2y}9\right\rangle \]
The Lagrange equations \(\nabla f_P = \lambda \nabla g_P\) are: \begin{equation*} \left\langle 2,5\right\rangle = \lambda \left\langle \frac{x}8, \frac{2y}9\right\rangle\quad\Rightarrow\quad 2 =\frac{\lambda x}8,\qquad 5 = \frac{\lambda (2y)}9\tag{2} \end{equation*}
Step 2. Solve for \(\lambda\) in terms of \(x\) and \(y\).
Eq. (2) gives us two equations for \(\lambda\): \begin{equation*} \lambda = \frac{16}{x},\qquad \lambda = \frac{45}{2 y}\tag{3} \end{equation*}
To justify dividing by \(x\) and \(y\), note that \(x\) and \(y\) must be nonzero, because \(x=0\) or \(y=0\) would violate Eq. (2).
Step 3. Solve for \(x\) and \(y\) using the constraint.
The two expressions for \(\lambda\) must be equal, so we obtain \(\frac{16}{x} = \frac{45}{2 y}\) or \(y = \frac{45}{32}x\). Now substitute this in the constraint equation and solve for \(x\): \[ \begin{array}{rl} \left(\frac{x}4\right)^2+\left(\frac{\frac{45}{32}x}{3}\right)^2 &=1\\ x^2\left(\frac{1}{16}+ \frac{225}{1024}\right)= x^2\left(\frac{289}{1024}\right) &=1 \end{array} \]
849
Thus \(x=\pm\sqrt{\tfrac{1024}{289}}=\pm \tfrac{32}{17}\), and since \(y = \tfrac{45x}{32}\), the critical points are \(P=\big(\frac{32}{17},\frac{45}{17}\big)\) and \(Q=\big(-\frac{32}{17},-\frac{45}{17}\big)\).
Step 4. Calculate the critical values.
\[ \begin{array}{rl} f(P) &= f\left(\frac{32}{17},\frac{45}{17}\right) = 2\left(\frac{32}{17}\right)+ 5\left(\frac{45}{17}\right) = 17 \end{array} \] and \(f(Q)=-17\). We conclude that the maximum of \(f(x,y)\) on the ellipse is \(17\) and the minimum is \(-17\) (Figure 14.72).
Assumptions Matter According to Theorem 3 in Section 14.7, a continuous function on a closed, bounded domain takes on extreme values. This tells us that if the constraint curve is bounded (as in the previous example, where the constraint curve is an ellipse), then every continuous function \(f(x,y)\) takes on both a minimum and a maximum value subject to the constraint. Be aware, however, that extreme values need not exist if the constraint curve is not bounded. For example, the constraint \(x-y=0\) is an unbounded line. The function \(f(x,y)=x\) has neither a minimum nor a maximum subject to \(x-y=0\) because \(P=(a,a)\) satisfies the constraint, yet \(f(a,a)=a\) can be arbitrarily large or small.
EXAMPLE 2 Cobb–Douglas Production Function
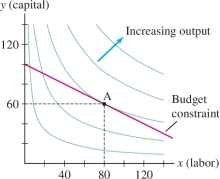
By investing \(x\) units of labor and \(y\) units of capital, a low-end watch manufacturer can produce \(P(x,y) = 50x^{0.4}y^{0.6}\) watches. (See Figure 14.73.) Find the maximum number of watches that can be produced on a budget of $20,000 if labor costs $100 per unit and capital costs $200 per unit.

Solution The total cost of \(x\) units of labor and \(y\) units of capital is \(100x + 200y\). Our task is to maximize the function \(P(x,y) = 50x^{0.4}y^{0.6}\) subject to the following budget constraint (Figure 14.74): \begin{equation*} g(x,y) = 100x+200y-20{,}000=0\tag{4} \end{equation*}
Step 1. Write out the Lagrange equations.
\[ \begin{array}{llll} &P_x(x,y)=\lambda g_x(x,y):&\quad 20x^{-0.6}y^{0.6} &= 100\lambda \\ &P_y(x,y)=\lambda g_y(x,y):&\quad 30x^{0.4}y^{-0.4} &= 200\lambda \end{array} \]
Step 2. Solve for \(\lambda\) in terms of \(x\) and \(y\).
These equations yield two expressions for \(\lambda\) that must be equal: \begin{equation*} \lambda = \frac15\left(\frac{y}x\right)^{0.6} = \frac{3}{20}\left(\frac{y}x\right)^{-0.4}\tag{5} \end{equation*}
Step 3. Solve for \(x\) and \(y\) using the constraint.
Multiply Eq. (5) by \(5(y/x)^{0.4}\) to obtain \(y/x =15/20\), or \(y = \tfrac34 x\). Then substitute in Eq. (4): \[ 100x+200y = 100x+200\left(\frac34 x\right) = 20{,}000\quad\Rightarrow\quad 250x = 20{,}000 \]
We obtain \(x = \tfrac{20{,}000}{250} = 80\) and \(y = \frac34 x = 60\). The critical point is \(A=(80,60)\).
Step 4. Calculate the critical values.
Since \(P(x,y)\) is increasing as a function of \(x\) and \(y\), \(\nabla P\) points to the northeast, and it is clear that \(P(x,y)\) takes on a maximum value at \(A\) (Figure 14.74). The maximum is \(P(80,60)= 50(80)^{0.4}(60)^{0.6} = 3365.87\), or roughly 3365 watches, with a cost per watch of \(\tfrac{20{,}000}{3365}\) or about $5.94.
850
GRAPHICAL INSIGHT
In an ordinary optimization problem without constraint, the global maximum value is the height of the highest point on the surface \(z = f(x,y)\) (point \(Q\) in Figure 14.75). When a constraint is given, we restrict our attention to the curve on the surface lying above the constraint curve \(g(x,y)=0\) . The maximum value subject to the constraint is the height of the highest point on this curve. Figure 14.75 shows the optimization problem solved in Example 1.
The method of Lagrange multipliers is valid in any number of variables. In the next example, we consider a problem in three variables.
EXAMPLE 3 Lagrange Multipliers in Three Variables
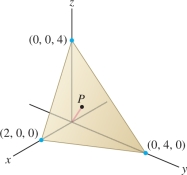
Find the point on the plane \(\frac{x}2+\frac{y}4+\frac{z}4=1\) closest to the origin in \({\bf{R}}^3\).
Solution Our task is to minimize the distance \(d=\sqrt{x^2+y^2+z^2}\) subject to the constraint \(\dfrac{x}2+\dfrac{y}4+\dfrac{z}4=1\). But finding the minimum distance \(d\) is the same as finding the minimum square of the distance \(d^2\), so our problem can be stated: \[ \textrm{Minimize } f(x,y,z)=x^2+y^2+z^2\quad\textrm{subject to }\quad g(x,y,z)=\dfrac{x}2+\dfrac{y}4+\dfrac{z}4-1=0 \]
The Lagrange condition is \[ \underbrace{\left\langle 2x, 2y, 2z\right\rangle}_{\nabla f} = \lambda \underbrace{\left\langle \frac12, \frac14, \frac14 \right\rangle}_{\nabla g} \]
This yields \[ \lambda = 4x=8y=8z\quad\Rightarrow\quad z=y=\frac x2 \]
Substituting in the constraint equation, we obtain \[ \frac{x}2+\frac{y}4+\frac{z}4= \frac{2z}2+\frac{z}4+\frac{z}4= \frac{3z}2= 1\quad \Rightarrow\quad z=\frac23 \]
Thus, \(x = 2z=\tfrac{4}{3}\) and \(y =z=\tfrac23\). This critical point must correspond to the minimum of \(f\) (because \(f\) has no maximum on the constraint plane). Hence, the point on the plane closest to the origin is \(P=\big(\frac43,\frac23,\frac23\big)\) (Figure 14.76).
851
The method of Lagrange multipliers can be used when there is more than one constraint equation, but we must add another multiplier for each additional constraint. For example, if the problem is to minimize \(f(x,y,z)\) subject to constraints \(g(x,y,z)=0\) and \(h(x,y,z)= 0\), then the Lagrange condition is \[ \nabla f = \lambda\nabla g + \mu\nabla h \]
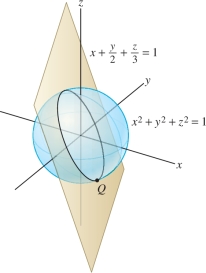
The intersection of a sphere with a plane through its center is called a great circle.
EXAMPLE 4 Lagrange Multipliers with Multiple Constraints
The intersection of the plane \(x+\tfrac12y+\tfrac13z=0\) with the unit sphere \(x^2+y^2+z^2=1\) is a great circle (Figure 14.77). Find the point on this great circle with the largest \(x\) coordinate.
Solution Our task is to maximize the function \(f(x,y,z)=x\) subject to the two constraint equations \[ g(x,y,z) = x+\frac12y+\frac13z = 0,\qquad h(x,y,z) = x^2+y^2+z^2-1 = 0 \]
The Lagrange condition is \[ \begin{array}{rl} \nabla f &= \lambda\nabla g + \mu\nabla h\\ \left\langle 1,0,0\right\rangle &= \lambda\left\langle 1,\frac12, \frac13 \right\rangle +\mu \left\langle 2x, 2y, 2z\right\rangle \end{array} \]
Note that \(\mu\) cannot be zero. The Lagrange condition would become \(\left\langle 1,0,0\right\rangle = \lambda \big\langle 1, \frac12, \frac13\big\rangle\), and this equation is not satisfed for any value of \(\lambda\). Now, the Lagrange condition gives us three equations: \[ \lambda+2\mu x = 1,\qquad \frac12\lambda+2\mu y=0,\qquad \frac13\lambda +2\mu z = 0 \]
The last two equations yield \(\lambda = -4\mu y\) and \(\lambda = -6\mu z\). Because \(\mu \neq 0\), \[ -4\mu y = -6\mu z\quad\Rightarrow\quad \boxed{y = \frac32 z} \]
Now use this relation in the first constraint equation: \[ x+\frac12y+\frac13z = x + \frac12\left(\frac32 z\right) + \frac13z = 0\quad\Rightarrow\quad \boxed{ x = -\frac{13}{12}z} \]
Finally, we can substitute in the second constraint equation: \[ x^2+y^2+z^2-1 = \left(-\frac{13}{12}z\right)^2 + \left(\frac32 z\right)^2 +z^2 - 1= 0 \] to obtain \(\tfrac{637}{144}z^2=1\) or \(z=\pm \tfrac{12}{7\sqrt{13}}\). Since \(x = -\frac{13}{12}z\) and \(y = \frac32 z\), the critical points are \[ P= \left(-\frac{\sqrt{13}}{7}, \frac{18}{7\sqrt{13}}, \frac{12}{7\sqrt{13}}\right),\qquad Q= \left(\frac{\sqrt{13}}{7}, -\frac{18}{7\sqrt{13}}, -\frac{12}{7\sqrt{13}}\right) \]
The critical point with the largest \(x\)-coordinate (the maximum value of \(f(x,y,z)\)) is \(Q\) with \(x\)-coordinate \(\tfrac{\sqrt{13}}{7}\approx 0.515\).
14.8.1 Summary
852
- Method of Lagrange multipliers: The local extreme values of \(f(x,y)\) subject to a constraint \(g(x,y)=0\) occur at points \(P\) (called critical points) satisfying the Lagrange condition \(\nabla f_P = \lambda \nabla g_P\). This condition is equivalent to the Lagrange equations \[ f_x(x,y)=\lambda g_x(x,y),\qquad f_y(x,y)=\lambda g_y(x,y) \]
- If the constraint curve \(g(x,y)=0\) is bounded [e.g., if \(g(x,y)=0\) is a circle or ellipse], then global minimum and maximum values of \(f\) subject to the constraint exist.
- Lagrange condition for a function of three variables \(f(x,y,z)\) subject to two constraints \(g(x,y,z)=0\) and \(h(x,y,z)=0\): \[ \nabla f = \lambda\nabla g + \mu\nabla h \]