15.5 Applications of Multiple Integrals

This section discusses some applications of multiple integrals. First, we consider quantities (such as mass, charge, and population) that are distributed with a given density \(\rho\) in \({\bf{R}}^2\) or \({\bf{R}}^3\). In single-variable calculus, we saw that the “total amount” is defined as the integral of density. Similarly, the total amount of a quantity distributed in \({\bf{R}}^2\) or \({\bf{R}}^3\) is defined as the double or triple integral: \begin{equation*} \boxed{\textrm{Total amount} = \iint_{\mathcal{D}}\,\rho(x,y)\,dA \quad\textrm{or}\quad \iiint_{\mathcal{W}}\,\rho(x,y,z)\,dV }\tag{1} \end{equation*}

The density function \(\rho\) has units of “amount per unit area” (or per unit volume).

The intuition behind Eq. (1) is similar to that of the single variable case. Suppose, for example, that \(\rho(x,y)\) is population density Figure 15.57. When density is constant, the total population is simply density times area: \[ \textrm{Population} = \textrm{density (people/km}^2)\times\textrm{area (km}^2) \]

To treat variable density in the case, say, of a rectangle \({\mathcal{R}}\), we divide \({\mathcal{R}}\) into smaller rectangles \({\mathcal{R}}_{ij}\) of area \(\Delta x\Delta y\) on which \(\rho\) is nearly constant (assuming that \(\rho\) is continuous on \({\mathcal{R}}\)). The population in \({\mathcal{R}}_{ij}\) is approximately \(\rho(P_{ij})\, \Delta x\Delta y\) for any sample point \(P_{ij}\) in \({\mathcal{R}}_{ij}\), and the sum of these approximations is a Riemann sum that converges to the double integral: \[ \int_{{\mathcal{R}}\,} \rho(x,y)\, dA \approx \sum_{i} \sum_{j} \rho(P_{ij})\Delta x\Delta y \]

908

EXAMPLE 1 Population Density

The population in a rural area near a river has density \[ \rho(x,y)=40xe^{0.1y} \textrm{ people per km}^2 \]

How many people live in the region \({\mathcal{R}}\): \(2\le x\le 6\), \(1\le y \le 3\) Figure 15.57?

Solution The total population is the integral of population density: \[ \begin{array}{rl} \iint_{{\mathcal{R}}} 40xe^{0.1y}\,dA &= \int_{2}^{6}\int_{1}^3 40xe^{0.1y} \,dx\,dy \\ &= \left(\int_{2}^{6} 40x \,dx \right)\left(\int_{1}^3 e^{0.1y} \,dy \right)\\ &= \left(20x^2 \Big|_{x=2}^6\right) \left(10e^{0.1y} \Big|_{y=1}^3\right) \approx (640)(2.447)\approx 1566\,\,\textrm{people} \end{array} \]

In the next example, we compute the mass of an object as the integral of mass density. In three dimensions, we justify this computation by dividing \({\mathcal{W}}\) into boxes \({\mathcal{B}}_{ijk}\) of volume \(\Delta V\) that are so small that the mass density is nearly constant on \({\mathcal{B}}_{ijk}\) Figure 15.58. The mass of \({\mathcal{B}}_{ijk}\) is approximately \(\rho(P_{ijk})\, \Delta V\), where \(P_{ijk}\) is any sample point in \({\mathcal{B}}_{ijk}\), and the sum of these approximations is a Riemann sum that converges to the triple integral: \[ \iiint_{{\mathcal{W}}\,} \rho(x,y,z)\,dV \approx \sum_{i} \sum_{j}\sum_{k} \underbrace{\rho(P_{ijk})\Delta V}_{\scriptsize\begin{array}{c}\mbox{Approximate mass}\\ \mbox{of }{\mathcal{B}}_{ijk}\end{array}} \]

When \(\rho\) is constant, we say that the solid has a uniform mass density. In this case, the triple integral has the value \(\rho V\) and the mass is simply \(M=\rho V\).

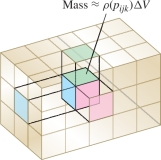
Figure 15.58: The mass of a small box is approximately \(\rho(P_{ijk})\,\Delta V\).

EXAMPLE 2

Let \(a>0\). Find the mass of the “solid bowl” \({\mathcal{W}}\) consisting of points inside the paraboloid \(z=a(x^2+y^2)\) for \(0\le z\le H\) Figure 15.59. Assume a mass density of \(\rho(x,y,z)=z\).

Figure 15.59: The paraboloid \(z=a(x^2+y^2)\).

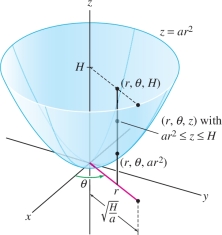
Solution Because the bowl is symmetric with respect to the \(z\)-axis, we use cylindrical coordinates \((r,\theta, z)\). Recall that \(r^2=x^2+y^2\), so the polar equation of the paraboloid is \(z=ar^2\). A point \((r,\theta, z)\) lies above the paraboloid if \(z\ge ar^2\), so it lies in the bowl if \(ar^2\le z \le H\). In other words, the bowl is described by \[ 0\le\theta\le 2\pi,\qquad 0\le r \le \sqrt{\frac{H}a},\qquad ar^2\le z \le H \]

The mass of the bowl is the integral of mass density: \[ \begin{array}{rl} M = \iiint_{{\mathcal{W}}\,} \rho(x,y,z)\,dV &= \int_{\theta = 0}^{2\pi}\int_{r=0}^{\sqrt{H/a}}\int_{z=ar^2}^{H} zr\,dz\,dr\,d\theta\\& = 2\pi \int_{r=0}^{\sqrt{H/a}} \left(\frac12H^2-\frac12a^2r^4\right)rdr\\ &= 2\pi \left(\frac{H^2r^2}4- \frac{a^2r^6}{12}\right)\Bigg|_{r=0}^{\sqrt{H/a}}\\ &= 2\pi\left(\frac{H^3}{4a}- \frac{H^3}{12a}\right) = \frac{\pi H^3}{3a} \end{array} \]

909

Next, we compute centers of mass. In Section 8.3, we computed centers of mass of laminas (thin plates in the plane), but we had to assume that the mass density is constant. Multiple integration enables us to treat variable mass density. We define the moments of a lamina \({\mathcal{D}}\) with respect to the coordinate axes: \[ M_y = \iint_{{\mathcal{D}}\,} x\rho(x,y)\,dA,\qquad M_x = \iint_{{\mathcal{D}}\,} y\rho(x,y)\,dA \]

The center of mass (COM) is the point \(P_{\mathrm{CM}}=(x_{\mathrm{CM}}, y_{\mathrm{CM}})\) where \begin{equation*} \boxed{x_{\mathrm{CM}} = \frac{M_y}{M},\qquad y_{\mathrm{CM}} = \frac{M_x}{M}}\tag{2} \end{equation*}

You can think of the coordinates \(x_{\mathrm{CM}}\) and \(y_{\mathrm{CM}}\) as weighted averages—they are the averages of \(x\) and \(y\) in which the factor \(\rho\) assigns a larger coefficient to points with larger mass density.

If \({\mathcal{D}}\) has uniform mass density (\(\rho\) constant), then the factors of \(\rho\) in the numerator and denominator in Eq. (2) cancel, and the center of mass coincides with the centroid, defined as the point whose coordinates are the averages of the coordinates over the domain: \[ \boxed{\overline x = \frac1{A} \,\iint_{{\mathcal{D}}\,} x\,dA,\qquad \overline y = \frac1{A}\,\iint_{{\mathcal{D}}\,} y\,dA } \]

Here \(A =\,\iint_{{\mathcal{D}}\,} 1\,dA \) is the area of \({\mathcal{D}}\).

  • In \({\bf{R}}^2\), we write \(M_y\) for the integral of \(x\rho(x,y)\) because \(x\) is the distance to the \(y\)-axis.
  • In \({\bf{R}}^3\), we write \(M_{yz}\) for the integral of \(x\rho(x,y,z)\) because in \({\bf{R}}^3\), \(x\) is the distance to the \(yz\)-plane.

In \({\bf{R}}^3\), the moments of a solid region \({\mathcal{W}}\) are defined not with respect to the axes as in \({\bf{R}}^2\), but with respect to the coordinate planes: \[ \begin{array}{rl} M_{yz} &= \iiint_{{\mathcal{W}}\,} x\rho(x,y,z)\,dV\\ M_{xz} &= \iiint_{{\mathcal{W}}\,} y\rho(x,y,z)\,dV\\ M_{xy} &= \iiint_{{\mathcal{W}}\,} z\rho(x,y,z)\,dV \end{array} \]

The center of mass is the point \(P_{\mathrm{CM}}=(x_{\mathrm{CM}}, y_{\mathrm{CM}}, z_{\mathrm{CM}})\) with coordinates \[ x_{\mathrm{CM}} = \frac{M_{yz}}{M},\qquad y_{\mathrm{CM}} = \frac{M_{xz}}{M},\qquad z_{\mathrm{CM}} = \frac{M_{xy}}{M} \]

The centroid of \({\mathcal{W}}\) is the point \(P = (\overline x, \overline y,\overline z)\), which, as before, coincides with the center of mass when \(\rho\) is constant: \[ \overline x = \frac1V \iiint_{{\mathcal{W}}\,} x \,dV ,\qquad \overline y = \frac1V\iiint_{{\mathcal{W}}\,} y \,dV ,\qquad \overline z = \frac1V\iiint_{{\mathcal{W}}\,} z \,dV \] where \(V =\,\iiint_{{\mathcal{W}}\,} 1\,dV \) is the volume of \({\mathcal{W}}\). Symmetry can often be used to simplify COM calculations. We say that a region \({\mathcal{W}}\) in \({\bf{R}}^3\) is symmetric with respect to the \(xy\)-plane if \((x,y,-z)\) lies in \({\mathcal{W}}\) whenever \((x,y,z)\) lies in \({\mathcal{W}}\).

The density \(\rho\) is symmetric with respect to the \(xy\)-plane if \[ \rho(x,y,-z)=\rho(x,y,z) \]

In other words, the mass density is the same at points located symmetrically with respect to the \(xy\)-plane. If both \({\mathcal{W}}\) and \(\rho\) have this symmetry, then \(M_{xy}=0\) and the COM lies on the \(xy\)-plane—that is, \(z_{\mathrm{CM}}=0\). Similar remarks apply to the other coordinate axes and to domains in the plane.

910

EXAMPLE 3 Center of Mass

Find the center of mass of the domain \({\mathcal{D}}\) bounded by \(y=1-x^2\) and the \(x\)-axis, assuming a mass density of \(\rho(x,y)=y\) Figure 15.60.

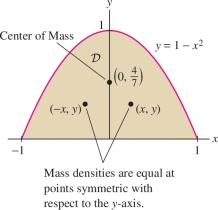
Solution The domain \({\mathcal{D}}\) is symmetric with respect to the \(y\)-axis, and so too is the mass density because \(\rho(x,y)=\rho(-x,y)=y\). Therefore, \(x_{\mathrm{CM}}=0\). We need only compute \(y_{\mathrm{CM}}\): \[ \begin{array}{rl} M_x&=\iint_{\mathcal{D}}\, y\rho(x,y)dA = \int_{x=-1}^1\int_{y=0}^{1-x^2}\,y^2\,dy\,dx = \int_{x=-1}^1\, \left(\frac13y^3\bigg|_{y=0}^{1-x^2}\right)\,dx\\ & = \frac13\int_{x=-1}^1\Big(1-3x^2+3x^4-x^6\Big)\,dx = \frac13\left(2-2+\frac65-\frac27\right) = \frac{32}{105}\\ M&=\iint_{\mathcal{D}}\rho(x,y)dA = \int_{x=-1}^1\int_{y=0}^{1-x^2}\,y\,dy\,dx = \int_{x=-1}^1\left(\frac12y^2\bigg|_{y=0}^{1-x^2}\right)\,dx\\ & = \frac12\int_{x=-1}^1\Big(1-2x^2+x^4\Big)\,dx = \frac12\left(2-\frac43+\frac25\right) = \frac8{15} \end{array} \]

Therefore, \(y_{\mathrm{CM}} = \frac{M_x}M= \frac{32}{105}\left(\frac8{15}\right)^{-1} = \frac47\).

EXAMPLE 4

Find the center of mass of the solid bowl \({\mathcal{W}}\) in Example 2 consisting of points inside the paraboloid \(z=a(x^2+y^2)\) for \(0\le z\le H\), assuming a mass density of \(\rho(x,y,z)=z\).

Solution The domain is shown in Figure 15.59 above.

Step 1. Use symmetry.

The bowl \({\mathcal{W}}\) and the mass density are both symmetric with respect to the \(z\)-axis, so we can expect the COM to lie on the \(z\)-axis. In fact, the density satisfies both \(\rho(-x,y,z) = \rho(x,y,z)\) and \(\rho(x,-y,z) = \rho(x,y,z)\), and thus we have \(M_{xz}=M_{yz}=0\). It remains to compute the moment \(M_{xy}\).

Step 2. Compute the moment.

In Example 2, we described the bowl in cylindrical coordinates as \[ 0\le\theta\le 2\pi,\qquad 0\le r \le \sqrt{\frac{H}a},\qquad ar^2\le z \le H \] and we computed the bowl’s mass as \(M = \frac{\pi H^3}{3a}\). The moment is \[ \begin{array}{rl} M_{xy} =\iiint_{{\mathcal{W}}\,} z\rho(x,y,z)\,dV = \iiint_{{\mathcal{W}}\,} z^2\,dV &= \int_{\theta = 0}^{2\pi}\int_{r=0}^{\sqrt{H/a}}\int_{z=ar^2}^{H} z^2r\,dz\,dr\,d\theta \\ &= 2\pi\int_{r=0}^{\sqrt{H/a}} \left(\frac13H^3- \frac13a^3r^6\right)r dr\\ &= 2\pi \left(\frac16H^3r^2 - \frac1{24}a^3r^8 \right)\Bigg|_{r=0}^{\sqrt{H/a}}\\ &= 2\pi\left( \frac{H^4}{6a} - \frac{a^3H^4}{24a^4}\right) = \frac{\pi H^4}{4a} \end{array} \]

The \(z\)-coordinate of the center of mass is \[ z_{CM} = \frac{M_{xy}}V = \frac{\pi H^4/(4a)}{\pi H^3/(3a)} = \frac34H \] and the center of mass itself is \(\big(0,0,\frac34H\big)\).

911

Moments of inertia are used to analyze rotation about an axis. For example, the spinning yo-yo in Figure 15.61 rotates about its center as it falls downward, and according to physics, it has a rotational kinetic energy equal to \[ \textrm{Rotational KE} = \frac12I\omega^2 \]

Figure 15.61: A spinning yo-yo has rotational kinetic energy \(\frac12I\omega^2\), where \(I\) is the moment of inertia and \(\omega\) is the angular velocity. See Exercise 47.

Here, \(\omega\) is the angular velocity (in radians per second) about this axis and \(I\) is the moment of inertia with respect to the axis of rotation. The quantity \(I\) is a rotational analog of the mass \(m\), which appears in the expression \(\frac12mv^2\) for linear kinetic energy.

By definition, the moment of inertia with respect to an axis \(L\) is the integral of “distance squared from the axis,” weighted by mass density. We confine our attention to the coordinate axes. Thus, for a lamina in the plane \({\bf{R}}^2\), we define the moments of inertia \begin{equation*} \boxed{\begin{array}{l} \displaystyle I_x = \iint_{{\mathcal{D}}\,} y^2\rho(x,y)\,dA\\ \displaystyle I_y = \iint_{{\mathcal{D}}\,} x^2\rho(x,y)\,dA\\ \displaystyle I_0 = \iint_{{\mathcal{D}}\,} (x^2+y^2)\rho(x,y)\,dA \end{array}}\tag{3} \end{equation*}

The quantity \(I_0\) is called the polar moment of inertia. It is the moment of inertia relative to the \(z\)-axis, because \(x^2+y^2\) is the square of the distance from a point in the \(xy\)-plane to the \(z\)-axis. Notice that \(I_0 =I_x+I_y\).

For a solid object occupying the region \({\mathcal{W}}\) in \({\bf{R}}^3\), \[ \boxed{\begin{array}{l} \displaystyle I_{x} = \iiint_{{\mathcal{W}}\,} (y^2+z^2)\rho(x,y,z)\,dV\\ \displaystyle I_{y} = \iiint_{{\mathcal{W}}\,} (x^2+z^2)\rho(x,y,z)\,dV\\ \displaystyle I_{z} = \iiint_{{\mathcal{W}}\,} (x^2+y^2)\rho(x,y,z)\,dV \end{array}} \]

Moments of inertia have units of mass times length-squared.

EXAMPLE 5

A lamina \({\mathcal{D}}\) of uniform mass density and total mass \(M\) kg occupies the region between \(y=1-x^2\) and the \(x\)-axis (in meters). Calculate the rotational KE if \({\mathcal{D}}\) rotates with angular velocity \(\omega = 4\) rad/s about:

  • (a) the \(x\)-axis
  • (b) the \(z\)-axis

Solution The lamina is shown in Figure 15.62. To find the rotational kinetic energy about the \(x\)- and \(z\)-axes, we need to compute \(I_x\) and \(I_0\), respectively.

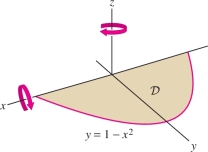
Figure 15.62: Rotating about the \(z\)-axis, the plate remains in the \(xy\)-plane. About the \(x\)-axis, it rotates out of the \(xy\)-plane.

Step 1. Find the mass density.

The mass density is uniform (that is, \(\rho\) is constant), but this does not mean that \(\rho = 1\). In fact, the area of \({\mathcal{D}}\) is \(\int_{-1}^1(1-x^2)\,dx = \tfrac43\), so the mass density (mass per unit area) is \[ \rho = \frac{\textrm{mass}}{\textrm{area}} = \frac{M}{\frac43} = \frac{3M}4\,\,\textrm{kg/m}^2 \]

912

Step 2. Calculate the moments.

\[ \begin{array}{rl} I_x &= \int_{-1}^{1}\int_{y=0}^{1-x^2} y^2\rho\,dy\,dx = \int_{-1}^{1}\frac13(1-x^2)^3\left(\frac{3M}4\right)\,dx \\ &= \frac{M}{4}\int_{-1}^{1}(1-3x^2+3x^4-x^6)\,dx = \frac{8M}{35} \,\,\textrm{kg-m}^2 \end{array} \]

To calculate \(I_0\), we use the relation \(I_0=I_x+I_y\). We have \[ I_y = \int_{-1}^{1}\int_{y=0}^{1-x^2} x^2\rho\,dy\,dx = \left(\frac{3M}4\right)\int_{-1}^{1}x^2(1-x^2)\,dx = \frac{M}5 \] and thus \begin{equation*} \begin{array}{rl} I_0 = I_x+I_y = \frac{8M}{35} + \frac{M}5 = \frac{3M}7 \end{array}\tag{4} \end{equation*}

CAUTION

The relation \[ I_0 = I_x + I_y \] is valid for a lamina in the \(xy\)-plane. However, there is no relation of this type for solid objects in \({\bf{R}}^3\).

Step 3. Calculate kinetic energy.

Assuming an angular velocity of \(\omega = 4\) rad/s, \[ \begin{array}{l} \textrm{Rotational KE about }x\textrm{-axis} = \frac12 I_x\omega^2 = \frac12\left(\frac{8M}{35}\right)4^2 \approx 1.8M\, \textrm{J}\\ \textrm{Rotational KE about }z\textrm{-axis} = \frac12 I_0\omega^2 = \frac12\left(\frac{3M}{7}\right)4^2 \approx 3.4M\, \textrm{J} \end{array} \]

The unit of energy is the joule (J), equal to 1 kg-m\(^2\)/s\(^2\).

A point mass \(m\) located a distance \(r\) from an axis has moment of inertia \(I = mr^2\) with respect to that axis. Given an extended object of total mass \(M\) (not necessarily a point mass) whose moment of inertia with respect to the axis is \(I\), we define the radius of gyration by \(r_g = (I/M)^{1/2}\). With this definition, the moment of inertia would not change if all of the mass of the object were concentrated at a point located a distance \(r_g\) from the axis.

EXAMPLE 6 Radius of Gyration of a Hemisphere

Find the radius of gyration about the \(z\)-axis of the solid hemisphere \({\mathcal{W}}\) defined by \(x^2+y^2+z^2=R^2\), \(0\le z \le 1\), assuming a mass density of \(\rho(x,y,z) = z\) kg/m\(^3\).

Solution To compute the radius of gyration about the \(z\)-axis, we must compute \(I_z\) and the total mass \(M\). We use spherical coordinates: \[ x^2+y^2 = (\rho\cos\theta\sin\phi)^2+(\rho\sin\theta\sin\phi)^2=\rho^2\sin^2\phi,\qquad z = \rho\cos\phi \] \[ \begin{array}{rl} I_z &= \iiint_{{\mathcal{W}}}(x^2+y^2)z \,dV = \int_{\theta = 0}^{2\pi}\int_{\phi = 0}^{\pi/2}\int_{\rho=0}^{R} (\rho^2\sin^2\phi)(\rho\cos\phi)\rho^2\sin\phi\, d\rho\,d\phi\,d\theta\\ &= 2\pi\left(\int_0^R\, \rho^5\,d\rho \right)\Bigg(\int_{\phi = 0}^{\pi/2} \sin^3\phi\cos\phi\, d\phi\Bigg)\\ &=2\pi\Bigg(\frac{R^6}6\Bigg)\Bigg(\frac{\sin^4\phi}4\bigg|_{0}^{\pi/2}\Bigg) = \frac{\pi R^6}{12}\,\textrm{kg-m}^2\\ M&= \iiint_{{\mathcal{W}}}z \,dV = \int_{\theta = 0}^{2\pi}\int_{\phi = 0}^{\pi/2}\int_{\rho=0}^{R} (\rho\cos\phi)\rho^2\sin\phi\, d\rho\,d\phi\,d\theta\\ &= \Bigg(\int_{\rho=0}^{R}\rho^3\,d\rho\Bigg)\Bigg(\int_{\phi = 0}^{\pi/2} \cos\phi\sin\phi \,d\phi\Bigg)\Bigg(\int_{\theta = 0}^{2\pi}\,d\theta\Bigg) =\frac{\pi R^4}4\,\textrm{kg} \end{array} \]

913

The radius of gyration is \(r_g = (I_z/M)^{1/2}=(R^2/3)^{1/2} = R/\sqrt{3}\) m.

Probability Theory

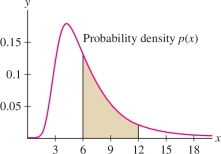
In Section 7.7, we discussed how probabilities can be represented as areas under curves Figure 15.63. Recall that a random variable \(X\) is defined as the outcome of an experiment or measurement whose value is not known in advance. The probability that the value of \(X\) lies between \(a\) and \(b\) is denoted \(P(a\le X \le b)\). Furthermore, \(X\) is a continuous random variable if there is a continuous function \(p(x)\), called the probability density function, such that Figure 15.63, \[ P(a\le X \le b) = \int_a^b\,p(x)\,dx \]

Figure 15.63: The shaded area is the probability that \(X\) lies between \(6\) and \(12\).

Double integration enters the picture when we compute “joint probabilities” of two random variables \(X\) and \(Y\). We let \[ P(a\le X \le b;\,\,c\le Y \le d) \] denote the probability that \(X\) and \(Y\) satisfy \[ a\le X \le b,\qquad c\le Y \le d \]

REMINDER

Conditions on a probability density function:

  • \(p(x)\ge 0\)
  • \(p(x)\) satisfies \(\int_{-\infty}^{\infty}p(x) = 1\)

For example, if \(X\) is the height (in centimeters) and \(Y\) is the weight (in kilograms) in a certain population, then \[ P(160\le X \le 170;\,\, 52\le Y \le 63) \] is the probability that a person chosen at random has height between \(160\) and \(170\) cm and weight between \(52\) and \(63\) kg.

We say that \(X\) and \(Y\) are jointly continuous if there is a continuous function \(p(x,y)\), called the joint probability density function (or simply the joint density), such that for all intervals \([a,b]\) and \([c,d]\) Figure 15.64, \[ P(a\le X \le b;c\le Y \le d) = \int_{x=a}^b\int_{y=c}^d\,p(x,y)\,dy\,dx \]

Figure 15.64: The probability \(P(a\le X \le b;c\le Y \le d)\) is equal to the integral of \(p(x,y)\) over the rectangle.

In the margin, we recall two conditions that a probability density function must satisfy. Joint density functions must satisfy similar conditions: First, \(p(x,y)\ge 0\) for all \(x\) and \(y\) (because probabilities cannot be negative), and second, \begin{equation*} \int_{-\infty}^\infty\int_{-\infty}^\infty p(x,y)\,dy\,dx=1\tag{5} \end{equation*}

This is often called the normalization condition. It holds because it is certain (the probability is 1) that \(X\) and \(Y\) take on some value between \(-\infty\) and \(\infty\).

EXAMPLE 7

Without proper maintenance, the time to failure (in months) of two sensors in an aircraft are random variables \(X\) and \(Y\) with joint density \[ p(x,y) = \left\{\begin{array}{ll} \frac1{864}e^{-x/24 -y/36}& \textrm{for }x\ge 0, y\ge 0 \\ \\ 0&\textrm{otherwise} \\ \end{array} \right. \]

What is the probability that neither sensor functions after two years?

914

Solution The problem asks for the probability \(P(0\le X\le 24;\, 0\le Y\le 24)\): \[ \begin{array}{rl} \int_{x=0}^{24}\int_{y=0}^{24}\,p(x,y)\,dy\,dx &= \frac1{864}\int_{x=0}^{24}\int_{y=0}^{24}\,e^{-x/24 -y/36}\,dy\,dx\\ &= \frac1{864}\Bigg(\int_{x=0}^{24}\,e^{-x/24}\,dx\Bigg)\Bigg(\int_{y=0}^{24}e^{-y/36}\,dy\Bigg)\\ &= \frac1{864}\Bigg(-24e^{-x/24}\Big|_0^{24}\Bigg)\Bigg(-36e^{-y/36}\Big|_0^{24}\Bigg)\\ & = \big(1-e^{-1}\big)\big(1 - e^{-24/36}\big)\approx 0.31 \end{array} \]

There is a 31% chance that neither sensor will function after two years.

More generally, we can compute the probability that \(X\) and \(Y\) satisfy conditions of various types. For example, \(P(X+Y\le M)\) denotes the probability that the sum \(X+Y\) is at most \(M\). This probability is equal to the integral \[ P(X+Y\le M) = \iint_{\mathcal{D}} p(x,y)\,dy\,dx \] where \({\mathcal{D}} = \{(x,y): x+y\le M\}\).

EXAMPLE 8

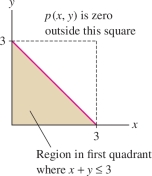
Calculate the probability that \(X+Y\le 3\), where \(X\) and \(Y\) have joint probability density \[ p(x,y) = \left\{\begin{array}{ll} \frac1{81}(2 xy + 2 x + y) & \textrm{for }0\le x\le 3,\,\, 0\le y\le 3 \\ \\ 0&\textrm{otherwise} \\ \end{array} \right. \]

Solution The probability density function \(p(x,y)\) is nonzero only on the square in Figure 15.65. Within that square, the inequality \(x+y\le 3\) holds only on the shaded triangle, so the probability that \(X+Y\le 3\) is equal to the integral of \(p(x,y)\) over the triangle: \[ \begin{array}{rl} \int_{x=0}^{3}\int_{y=0}^{3-x}\,p(x,y)\,dy\,dx &=\frac1{81}\int_{x=0}^{3} \Bigg(xy^2+\frac12y^2 +2xy\Bigg)\Bigg|_{y=0}^{3-x}\,dx\\ &=\frac1{81}\int_{x=0}^{3} \Bigg(x^3 -\frac{15}2 x^2 +12x + \frac92\Bigg) \,dx\\ &= \frac1{81}\Bigg(\frac143^4-\frac{5}23^3+6(3^2) +\frac{9}2(3)\Bigg) = \frac14 \end{array} \]

15.5.1 Summary

915

In \({\bf{R}}^2\) In \({\bf{R}}^3\)
Total mass \(M = \iint_{{\mathcal{D}}\,}\rho(x,y)\,dA\) \(M = \iiint_{{\mathcal{W}}\,}\rho(x,y,z)\,dV\)
Moments \[ \begin{array}{l} M_x = \iint_{{\mathcal{D}}\,}y\rho(x,y)\,dA\\ M_y = \iint_{{\mathcal{D}}\,}x\rho(x,y)\,dA \end{array} \] \[ \begin{array}{l} M_{yz} = \iiint_{{\mathcal{W}}\,}x\rho(x,y,z)\,dV\\ M_{xz} = \iiint_{{\mathcal{W}}\,}y\rho(x,y,z)\,dV\\ M_{xy} = \iiint_{{\mathcal{W}}\,}z\rho(x,y,z)\,dV \end{array} \]
Center of Mass \(x_{\mathrm{CM}} = \frac{M_y}{M}\), \(y_{\mathrm{CM}} = \frac{M_x}{M}\) \(x_{\mathrm{CM}} = \frac{M_{yz}}{M}\), \(y_{\mathrm{CM}} = \frac{M_{xz}}{M}\), \(z_{\mathrm{CM}} = \frac{M_{xy}}{M}\)
Moments of Inertia \[ \begin{array}{l} I_x = \iint_{{\mathcal{D}}\,}y^2\rho(x,y)\,dA\\ I_y = \iint_{{\mathcal{D}}\,}x^2\rho(x,y)\,dA\\ I_0 = \iint_{{\mathcal{D}}\,}(x^2+y^2)\rho(x,y)\,dA\\ (I_0= I_x + I_y) \end{array} \] \[ \begin{array}{l} I_x = \iiint_{{\mathcal{W}}\,}(y^2+z^2)\rho(x,y,z)\,dV\\ I_y = \iiint_{{\mathcal{W}}\,}(x^2+z^2)\rho(x,y,z)\,dV\\ I_z = \iiint_{{\mathcal{W}}\,}(x^2+y^2)\rho(x,y,z)\,dV \end{array} \]