16.1 Vector Fields
How can we describe a physical object such as the wind, that consists of a large number of molecules moving in a region of space? What we need is a new mathematical object called a vector field. A vector field \({\bf{F}}\) assigns to each point \(P\) a vector \({\bf{F}}(P)\) that represents the velocity (speed and direction) of the wind at that point (Figure 16.1). Another velocity field is shown in Figure 16.2. However, vector fields describe many other types of quantities, such as forces, and electric and magnetic fields.

Mathematically, a vector field in \({\bf{R}}^3\) is represented by a vector whose components are functions: \[ {\bf{F}}(x,y,z) = \left\langle F_1(x,y,z), F_2(x,y,z), F_3(x,y,z)\right\rangle \]
To each point \(P=(a,b,c)\) is associated the vector \({\bf{F}}(a,b,c)\), which we also denote by \({\bf{F}}(P)\). Alternatively, \[ {\bf{F}} = F_1{\bf{i}}+F_2{\bf{j}}+F_3{\bf{k}} \]
When drawing a vector field, we draw \({\bf{F}}(P)\) as a vector based at \(P\) (rather than the origin). The domain of \({\bf{F}}\) is the set of points \(P\) for which \({\bf{F}}(P)\) is defined. Vector fields in the plane are written in a similar fashion: \[ {\bf{F}}(x,y)=\left\langle F_1(x,y), F_2(x,y)\right\rangle = F_1{\bf{i}}+F_2{\bf{j}} \]
Throughout this chapter, we assume that the component functions \(F_j\) are smooth—that is, they have partial derivatives of all orders on their domains.
940
EXAMPLE 1
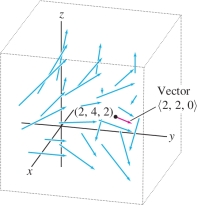
Which vector is attached to the point \(P = (2,4,2)\) by the vector field \({\bf{F}} = \left\langle y-z, x, z-\sqrt{y}\right\rangle\)?
Solution The vector attached to \(P\) is \[ {\bf{F}}(2,4,2) = \left\langle 4-2, 2, 2-\sqrt{4}\right\rangle = \left\langle 2, 2, 0\right\rangle \]
This is the red vector in Figure 16.3.
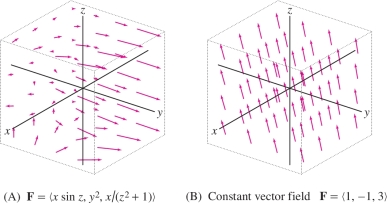
Although it is not practical to sketch complicated vector fields in three dimensions by hand, computer algebra systems can produce useful visual representations (Figure 16.4). The vector field in Figure 16.4 is an example of a constant vector field. It assigns the same vector \(\left\langle 1,-1,3 \right\rangle\) to every point in \({\bf{R}}^3\).
In the next example, we analyze two vector fields in the plane “qualitatively.”
EXAMPLE 2
Describe the following vector fields:
- (a) \({\bf{G}} = {\bf{i}} + x{\bf{j}}\)
- (b) \({\bf{F}}=\left\langle -y,x\right\rangle\)
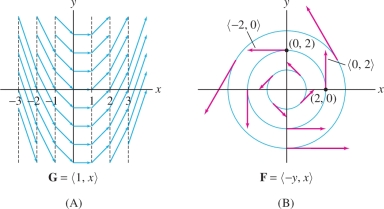
Solution (a) The vector field \({\bf{G}} = {\bf{i}} + x{\bf{j}}\) assigns the vector \(\left\langle 1,a\right\rangle\) to the point \((a,b)\). In particular, it assigns the same vector to all points with the same \(x\)-coordinate [Figure~5(A)]. Notice that \(\left\langle 1,a\right\rangle\) has slope \(a\) and length \(\sqrt{1+a^2}\). We may describe \({\bf{G}}\) as follows: \({\bf{G}}\) assigns a vector of slope \(a\) and length \(\sqrt{1+a^2}\) to all points with \(x=a\).
(b) To visualize \({\bf{F}}\), observe that \({\bf{F}}(a,b) = \left\langle -b,a\right\rangle\) has length \(r=\sqrt{a^2+b^2}\). It is perpendicular to the radial vector \(\left\langle a,b\right\rangle\) and points counterclockwise. Thus \({\bf{F}}\) has the following description: The vectors along the circle of radius \(r\) all have length \(r\) and they are tangent to the circle, pointing counterclockwise [Figure 16.5].

941
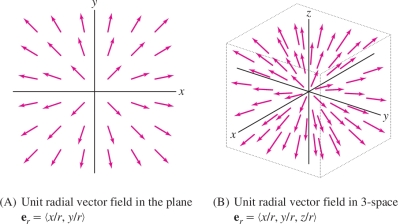
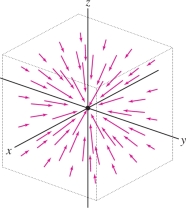
A unit vector field is a vector field \({\bf{F}}\) such that \(\left \| {{\bf{F}}(P)} \right \|=1\) for all points \(P\). A vector field \({\bf{F}}\) is called a radial vector field if \({\bf{F}}(P)\) depends only on the distance \(r\) from \(P\) to the origin. Here we use the notation \(r=(x^2+y^2)^{1/2}\) for \(n=2\) and \(r=(x^2+y^2+z^2)^{1/2}\) for \(n=3\). Two important examples are the unit radial vector fields in two and three dimensions (Figure 16.6): \begin{equation} {\bf{e}}_r = \left\langle\frac{x}r, \frac{y}r\right\rangle = \left\langle\frac{x}{\sqrt{x^2+y^2}}, \frac{y}{\sqrt{x^2+y^2}}\right\rangle \end{equation} \begin{equation} {\bf{e}}_r = \left\langle\frac{x}r, \frac{y}r, \frac{z}r\right\rangle = \left\langle\frac{x}{\sqrt{x^2+y^2+z^2}}, \frac{y}{\sqrt{x^2+y^2+z^2}}, \frac{z}{\sqrt{x^2+y^2+z^2}}\right\rangle \end{equation}
Observe that \({\bf{e}}_r(P)\) is a unit vector pointing away from the origin at \(P\). Note, however, that \({\bf{e}}_r\) is not defined at the origin where \(r=0\).
Conservative Vector Fields
We already encountered one type of vector field in Chapter 15—namely, the gradient vector field of a differentiable function \({V}(x,y,z)\): \[ {\bf{F}}= \nabla{V} = \left\langle \frac{\partial {V}}{\partial x},\frac{\partial {V}}{\partial y},\frac{\partial {V}}{\partial z}\right\rangle \]
A vector field of this type is called a conservative vector field, and the function \({V}\) is called a potential function (or scalar potential function) for \({\bf{F}}\).
- The term “conservative” comes from physics and the law of conservation of energy (see Section 16.3).
- Any letter can be used to denote a potential function. We use \(V\), which suggests “volt,” the unit of electric potential. Some textbooks use \(\phi(x,y,z)\) or \(U(x,y,z)\), or simply \(f(x,y,z)\).
- Theorem 1 is valid for a vector field in the plane \({\bf{F}} = \left\langle F_1,F_2\right\rangle\). If \({\bf{F}}=\nabla{V}\), then \(\frac{\partial F_1}{\partial y} = \frac{\partial F_2}{\partial x}\).
The same terms apply in two variables and, more generally, in \(n\) variables. Recall that the gradient vectors are orthogonal to the level curves, and thus in a conservative vector field, the vector at every point \(P\) is orthogonal to the level curve through \(P\) (Figure 16.7).

EXAMPLE 3
Verify that \({V}(x,y,z)=xy+yz^2\) is a potential function for the vector field \({\bf{F}} = \big\langle y,x+ z^2,2yz\big\rangle\).
Solution We compute the gradient of \({V}\): \[ \frac{\partial {V}}{\partial x} =y,\quad \frac{\partial {V}}{\partial y} =x+z^2,\quad\frac{\partial {V}}{\partial z}=2yz \]
Thus, \(\nabla{V} = \big\langle y,x+z^2,2yz\big\rangle = {\bf{F}}\) as claimed.
942
Conservative vector fields have a special property: They satisfy the cross-partial condition.
THEOREM 1 Cross-Partial Property of a Conservative Vector Field
If the vector field \({\bf{F}} = \left\langle F_1, F_2, F_3\right\rangle\) is conservative, then \[ \boxed{\frac{\partial F_1}{\partial y} = \frac{\partial F_2}{\partial x},\quad \frac{\partial F_2}{\partial z} = \frac{\partial F_3}{\partial y},\quad \frac{\partial F_3}{\partial x} = \frac{\partial F_1}{\partial z}} \]
Proof If \({\bf{F}} = \nabla{V}\), then \[ F_1 = \frac{\partial {V}}{\partial x}, \quad F_2 = \frac{\partial {V}}{\partial y}, \quad F_3 = \frac{\partial {V}}{\partial z} \]
Now compare the “cross”-partial derivatives: \[ \begin{array}{rl} \frac{\partial F_1}{\partial y} &= \frac{\partial }{\partial y}\left(\frac{\partial {V}}{\partial x}\right)= \frac{\partial ^2{V}}{\partial y\partial x}\\ \frac{\partial F_2}{\partial x} &= \frac{\partial }{\partial x}\left(\frac{\partial {V}}{\partial y}\right)= \frac{\partial ^2{V}}{\partial x\partial y} \end{array} \]
Clairaut’s Theorem (Section 14.3) tells us that \(\frac{\partial ^2{V}}{\partial y\,\partial x}= \frac{\partial ^2{V}}{\partial x\,\partial y}\), and thus \[ \frac{\partial F_1}{\partial y} = \frac{\partial F_2}{\partial x} \]
Similarly, \(\frac{\partial F_2}{\partial z} = \frac{\partial F_3}{\partial y}\) and \(\frac{\partial F_3}{\partial x} = \frac{\partial F_1}{\partial z}\).
From Theorem 1, we can see that most vector fields are not conservative. Indeed, an arbitrary triple of functions \(\left\langle F_1, F_2, F_3\right\rangle\) does not satisfy the cross-partials condition. Here is an example.
EXAMPLE 4
Show that \({\bf{F}} = \left\langle y, 0, 0\right\rangle\) is not conservative.
Solution We have \[ \frac{\partial F_1}{\partial y} = \frac{\partial }{\partial y}y=1,\qquad \frac{\partial F_2}{\partial x} = \frac{\partial }{\partial x}0 = 0 \]
Thus \(\frac{\partial F_1}{\partial y} \ne \frac{\partial F_2}{\partial x}\). By Theorem 1, \({\bf{F}}\) is not conservative, even though the other cross-partials agree: \[ \frac{\partial F_3}{\partial x} = \frac{\partial F_1}{\partial z} =0\qquad\textrm{and}\qquad \frac{\partial F_2}{\partial z} = \frac{\partial F_3}{\partial y} =0 \]
Potential functions, like antiderivatives in one variable, are unique to within an additive constant. To state this precisely, we must assume that the domain \({\mathcal{D}}\) of the vector field is open and connected (Figure 16.8). “Connected” means that any two points can be joined by a path within the domain.
943
THEOREM 2 Uniqueness of Potential Functions
If \({\bf{F}}\) is conservative on an open connected domain, then any two potential functions of \({\bf{F}}\) differ by a constant.
Proof If both \({V}_1\) and \({V}_2\) are potential functions of \({\bf{F}}\), then \[ \nabla({V}_1-{V}_2) = \nabla{V}_1 -\nabla{V}_2 = {\bf{F}}-{\bf{F}} = \mathbf{0} \]
However, a function whose gradient is zero on an open connected domain is a constant function (this generalizes the fact from single-variable calculus that a function on an interval with zero derivative is a constant function—see Exercise 36). Thus \({V}_1-{V}_2=C\) for some constant \(C\), and hence \({V}_1={V}_2+C\).
The next two examples consider two important radial vector fields.
The result of Example 5 is valid in \({\bf{R}}^2\): The function \[ V(x,y) = \sqrt{x^2+y^2} = r \] is a potential function for \({\bf{e}}_r\).
EXAMPLE 5 Unit Radial Vector Fields
Show that \[ V(x,y,z)=r=\sqrt{x^2+y^2+z^2} \] is a potential function for \({\bf{e}}_r\). That is, \({\bf{e}}_r = \nabla r\).
Solution We have \[ \frac{\partial r}{\partial x} = \frac{\partial}{\partial x} \sqrt{x^2+y^2+z^2} = \frac{x}{\sqrt{x^2+y^2+z^2}}=\frac xr \]
Similarly, \(\frac{\partial r}{\partial y} = \frac{y}r\) and \(\frac{\partial r}{\partial z} = \frac{z}r\). Therefore, \(\nabla r = \left\langle \frac{x}r, \frac{y}r, \frac{z}r\right\rangle = {\bf{e}}_r\).
The gravitational force exerted by a point mass \(m\) is described by an inverse-square force field (Figure 16.9). A point mass located at the origin exerts a gravitational force \({\bf{F}}\) on a unit mass located at \((x,y,z)\) equal to \[ {\bf{F}}= -\frac{Gm}{r^2}{\bf{e}}_r = -Gm\left\langle \frac{x}{r^3}, \frac{y}{r^3}, \frac{z}{r^3}\right\rangle \] where \(G\) is the universal gravitation constant. The minus sign indicates that the force is attractive (it pulls in the direction of the origin). The electrostatic force field due to a charged particle is also an inverse-square vector field. The next example shows that these vector fields are conservative.
REMINDER
\[ {\bf{e}}_r = \left\langle \frac{x}{r}, \frac{y}{r}, \frac{z}{r}\right\rangle \] where \[ r=(x^2+y^2+z^2)^{1/2} \]
In \({\bf{R}}^2\), \[ {\bf{e}}_r = \left\langle \frac{x}{r}, \frac{y}{r}\right\rangle \] where \(r=(x^2+y^2)^{1/2}\).
EXAMPLE 6 Inverse-Square Vector Field
Show that \[ \frac{{\bf{e}}_r}{r^2}=\nabla\left(\frac{-1}{r}\right) \]
Solution Use the Chain Rule for gradients (Theorem 1 in Section 14.5) and Example 5: \[ \nabla(-r^{-1})=r^{-2}\nabla r=r^{-2}{\bf{e}}_r \]
16.1.1 Summary
- A vector field assigns a vector to each point in a domain. A vector field in \({\bf{R}}^3\) is represented by a triple of functions \[ {\bf{F}}=\left\langle F_1, F_2, F_3\right\rangle \] A vector field in \({\bf{R}}^2\) is represented by a pair of functions \({\bf{F}} = \left\langle F_1, F_2\right\rangle\). We always assume that the components \(F_j\) are smooth functions on their domains.
- If \({\bf{F}} = \nabla {V}\), then \({V}\) is called a potential function for \({\bf{F}}\).
- \({\bf{F}}\) is called conservative if it has a potential function.
- Any two potential functions for a conservative vector field differ by a constant (on an open, connected domain).
- A conservative vector field \({\bf{F}}\) satisfies the cross-partial condition: \[ \frac{\partial F_1}{\partial y}=\frac{\partial F_2}{\partial x},\qquad \frac{\partial F_2}{\partial z}=\frac{\partial F_3}{\partial y}, \qquad\frac{\partial F_3}{\partial x}=\frac{\partial F_1}{\partial z} \]
- We define \[ r=\sqrt{x^2+y^2}\quad(\textrm{in } {\bf{R}}^2),\qquad\quad r = \sqrt{x^2+y^2+z^2}\quad(\textrm{in } {\bf{R}}^3) \]
- The radial unit vector field and the inverse-square vector field are conservative: \[ {\bf{e}}_r = \left\langle \frac xr,\frac yr,\frac zr \right\rangle = \nabla r,\qquad \frac{{\bf{e}}_r}{r^2} = \left\langle \frac{x}{r^3},\frac{y}{r^3},\frac{z}{r^3} \right\rangle = \nabla (-r^{-1}) \]
944