17.3 SUMMARY

• We have two notations for the line integral of a vector field: \[ \int_{C} {\bf F}\cdot d{\bf s}\qquad \textrm{and}\qquad \int_{C} F_1\,dx+F_2\,dy \]
• \(\partial D\) denotes the boundary of \(D\) with its boundary orientation (Figure 17.15).
  

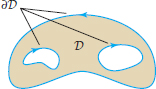  Figure 17.15: The boundary orientation is chosen so that the region lies to your left as you walk along the curve.
• Green’s Theorem: \[ \oint_{\partial D} F_1\,dx+F_2\,dy = \iint_{D\,}\left(\dfrac{\partial{F_2}}{\partial{x}}-\dfrac{\partial{F_1}}{\partial{y}}\right)\,dA \]
• Formula for the area of the region \(D\) enclosed by \(C\): \[ \textrm{Area}(D) = \frac12\oint_C x\,dy-y\,dx \]
• The quantity \[ {{\bf curl}_z({\bf F}) = \dfrac{\partial{F_2}}{\partial{x}}-\dfrac{\partial{F_1}}{\partial{y}}} \] is interpreted as circulation per unit area. If \(D\) is a small domain with boundary \(C\), then for any \(P\in D\), \[ \oint_{C} F_1\,dx+F_2\,dy\approx {\bf curl}_z({\bf F})(P)\cdot\textrm{Area}(D) \]