17.4 EXERCISES
Preliminary Questions
Question 17.1
Which vector field \({\bf F}\) is being integrated in the line integral \(\displaystyle{\oint x^2\,dy-e^y\,dx}\)?
Question 17.2
Draw a domain in the shape of an ellipse and indicate with an arrow the boundary orientation of the boundary curve. Do the same for the annulus (the region between two concentric circles).
Question 17.3
The circulation of a conservative vector field around a closed curve is zero. Is this fact consistent with Green’s Theorem? Explain.
Question 17.4
Indicate which of the following vector fields possess the following property: For every simple closed curve \(C\), \(\displaystyle{\int_{C} {\bf F}\cdot d{\bf s}}\) is equal to the area enclosed by \(C\).
- (a) \({\bf F}=\langle -y,0\rangle\)
- (b) \({\bf F}=\langle x,y\rangle\)
- (c) \({\bf F}=\langle \sin(x^2),x+e^{y^2}\rangle\)
Exercises
Question 17.5
Verify Green’s Theorem for the line integral \(\displaystyle{\oint_C xy\,dx+y\,dy}\), where \(C\) is the unit circle, oriented counterclockwise.
Question 17.6
Let \(\displaystyle{I=\oint_C {\bf F}\cdot d{\bf s}}\), where \({\bf F}=\langle y+\sin x^2,x^2+e^{y^2} \rangle\) and \(C\) is the circle of radius 4 centered at the origin.
- (a) Which is easier, evaluating \(I\) directly or using Green’s Theorem?
- (b) Evaluate \(I\) using the easier method.
In Exercises 3–10, use Green’s Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwise indicated.
Question 17.7
\(\displaystyle{\oint_C y^2\,dx + x^2\,dy}\), where \(C\) is the boundary of the unit square \(0\le x \le 1\), \(0\le y \le 1\)
Question 17.8
\(\displaystyle{\oint_C e^{2x+y}\,dx + e^{-y}\,dy}\), where \(C\) is the triangle with vertices \((0,0)\), \((1,0)\), and \((1,1)\)
Question 17.9
\(\displaystyle{\oint_C x^2\,y\,dx}\), where \(C\) is the unit circle centered at the origin
Question 17.10
\(\displaystyle{\oint_C {\bf F} \cdot d{\bf s}}\), where \({\bf F}=\langle x+y,x^2-y \rangle\) and \(C\) is the boundary of the region enclosed by \(y=x^2\) and \(y=\sqrt{x}\) for \(0\le x \le 1\)
Question 17.11
\(\displaystyle{\oint_C {\bf F} \cdot d{\bf s}}\), where \({\bf F} = \langle x^2, x^2\rangle\) and \(C\) consists of the arcs \( y = x^2\) and \(y=x\) for \(0\le x \le 1\)
Question 17.12
\(\displaystyle{\oint_C (\ln x+y)\,dx - x^2\,dy}\), where \(C\) is the rectangle with vertices \((1,1)\), \((3,1)\), \((1,4)\), and \((3,4)\)
Question 17.13
The line integral of \({\bf F}=\langle e^{x+y},e^{x-y} \rangle\) along the curve (oriented clockwise) consisting of the line segments by joining the points \((0,0)\), \((2,2)\), \((4,2)\), \((2,0)\), and back to \((0,0)\) (note the orientation).
Question 17.14
\(\displaystyle{\int_{C} xy\,dx+(x^2+x)\,dy}\), where \(C\) is the path in Figure 17.16
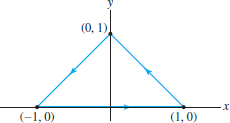
Question 17.15
Let \({\bf F} = \langle 2xe^y,x+x^2e^y\rangle\) and let \(C\) be the quarter-circle path from \(A\) to \(B\) in Figure 17.17. Evaluate \(\displaystyle{I=\oint_C {\bf F}\cdot d{\bf s}}\) as follows:
- (a) Find a function \(V(x,y)\) such that \({\bf F} = {\bf G}+\nabla V\), where \({\bf G}=\langle 0,x\rangle\).
- (b) Show that the line integrals of \({\bf G}\) along the segments \(\overline{OA}\) and \(\overline{OB}\) are zero.
- (c) Evaluate \(I\). Hint: Use Green’s Theorem to show that
\[
I = V(B)-V(A) + 4\pi
\]
1012
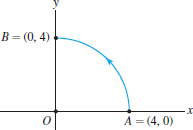
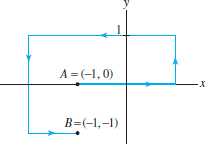
Question 17.16
Compute the line integral of \({\bf F} = \langle x^3, 4x\rangle\) along the path from \(A\) to \(B\) in Figure 17.18. To save work, use Green’s Theorem to relate this line integral to the line integral along the vertical path from \(B\) to \(A\).
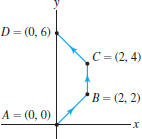
Question 17.17
Evaluate \(\displaystyle{I=\int_{C} (\sin x + y)\,dx+(3x+y)\,dy}\) for the nonclosed path ABCD in Figure 17.19. Use the method of Exercise 12.
Question 17.18
Show that if \(C\) is a simple closed curve, then \[ \oint_C -y\,dx = \oint_C x\,dy \] and both integrals are equal to the area enclosed by \(C\).
In Exercises 15–18, use Eq. (6) to calculate the area of the given region.
Question 17.19
The circle of radius 3 centered at the origin
Question 17.20
The triangle with vertices \((0,0)\), \((1,0)\), and \((1,1)\)
Question 17.21
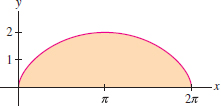
The region between the \(x\)-axis and the cycloid parametrized by \({\bf c}(t) = (t-\sin t, 1-\cos t)\) for \(0\le t \le 2\pi\) (Figure 17.20)
Question 17.22
The region between the graph of \(y=x^2\) and the \(x\)-axis for \(0\le x \le 2\)
Question 17.23
Let \(x^3+y^3=3xy\) be the folium of Descartes (Figure 17.21).

- (a) Show that the folium has a parametrization in terms of \(t=y/x\) given by \[ x=\frac{3t}{1+t^3},\qquad y = \frac{3t^2}{1+t^3} \quad (-\infty<t<\infty)\quad (t \ne -1) \]
- (b) Show that \[ x\,dy-y\,dx = \frac{9t^2}{(1+t^3)^2}\,dt \] Hint: By the Quotient Rule, \[ x^2\,d\left(\frac{y}x\right) = x\,dy-y\,dx \]
- (c) Find the area of the loop of the folium.
Question 17.24
Find a parametrization of the lemniscate \((x^2 + y^2)^2 = xy\) (see Figure 17.22) by using \(t=y/x\) as a parameter (see Exercise 19). Then use Eq. (6) to find the area of one loop of the lemniscate.
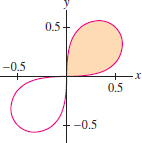
1013
Question 17.25
The Centroid via Boundary Measurements The centroid (see Section 15.5) of a domain \(D\) enclosed by a simple closed curve \(C\) is the point with coordinates \((\overline x,\overline y) = (M_y/M, M_x/M)\), where \(M\) is the area of \(D\) and the moments are defined by \[ M_x = \iint_{D}y\,dA,\qquad M_y = \iint_{D}x\,dA \] Show that \(\displaystyle{M_x = \oint_{C} xy\,dy}\). Find a similar expression for \(M_y\).
Question 17.26
Use the result of Exercise 21 to compute the moments of the semicircle \(x^2+y^2=R^2\), \(y\ge 0\) as line integrals. Verify that the centroid is \((0,4R/(3\pi))\).
Question 17.27
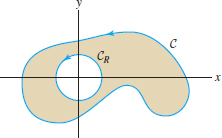
Let \(C_R\) be the circle of radius \(R\) centered at the origin. Use the general form of Green’s Theorem to determine \(\displaystyle{\oint_{C_2}{\bf F}\cdot d{\bf s}}\), where \({\bf F}\) is a vector field such that \(\displaystyle{\oint_{C_1}{\bf F}\cdot d{\bf s}=9}\) and \(\displaystyle{\dfrac{\partial{F_2}}{\partial{x}}-\dfrac{\partial{F_1}}{\partial{y}} =x^2+y^2}\) for \((x,y)\) in the annulus \(1 \le x^2+y^2 \le 4\).
Question 17.28
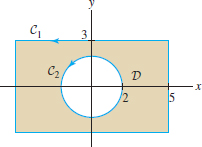
Referring to Figure 17.23, suppose that \(\displaystyle{\oint_{C_2}{\bf F} \cdot d{\bf s} = 12}\). Use Green’s Theorem to determine \(\displaystyle{\int_{C_1}{\bf F}\cdot d{\bf s}}\), assuming that \(\displaystyle{\dfrac{\partial{F_2}}{\partial{x}}-\dfrac{\partial{F_1}}{\partial{x}} =-3}\) in \(D\).
Question 17.29
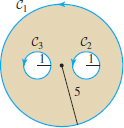
Referring to Figure 17.24, suppose that \[ \oint_{C_2}{\bf F} \cdot d{\bf s} = 3\pi,\qquad \oint_{C_3}{\bf F} \cdot d{\bf s} = 4\pi \] Use Green’s Theorem to determine the circulation of \({\bf F}\) around \(C_1\), assuming that \(\displaystyle{\dfrac{\partial{F_2}}{\partial{x}}-\dfrac{\partial{F_1}}{\partial{x}}=9}\) on the shaded region.
Question 17.30
Let \(\displaystyle{{\bf F}}\) be the vortex vector field \[ {\bf F} = \langle \frac{-y}{x^2+y^2}, \frac{x}{x^2+y^2}\rangle \] In Section 16.3 we verified that \(\displaystyle{\int_{C_R}\,{\bf F}\cdot\,d{\bf s} = 2\pi}\), where \(C_R\) is the circle of radius \(R\) centered at the origin. Prove that \(\displaystyle{\oint_{C}{\bf F}\cdot d{\bf s} = 2\pi}\) for any simple closed curve \(C\) whose interior contains the origin (Figure 17.25). Hint: Apply the general form of Green’s Theorem to the domain between \(C\) and \(C_R\), where \(R\) is so small that \(C_R\) is contained in \(C\).
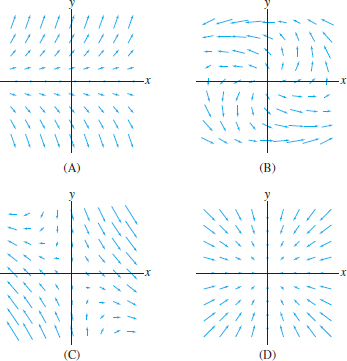
In Exercises 27–30, refer to the Conceptual Insight that discusses the curl, defined by \[ {\bf curl}_z({\bf F}) = \dfrac{\partial{F_2}}{\partial{x}} - \dfrac{\partial{F_1}}{\partial{y}} \]
Question 17.31
For the vector fields (A)–(D) in Figure 17.26, state whether the \({\bf curl}_z\) at the origin appears to be positive, negative, or zero.
1014
Question 17.32
Estimate the circulation of a vector field \({\bf F}\) around a circle of radius \(R=0.1\), assuming that \({\bf curl}_z({\bf F})\) takes the value 4 at the center of the circle.
Question 17.33
Estimate \(\displaystyle{\oint_{C}\,{\bf F}\cdot\,d{\bf s}}\), where \({\bf F} = \langle x+0.1y^2,y-0.1x^2\rangle\) and \(C\) encloses a small region of area \(0.25\) containing the point \(P=(1,1)\).
Question 17.34
Let \({\bf F}\) be the velocity field. Estimate the circulation of \({\bf F}\) around a circle of radius \(R=0.05\) with center \(P\), assuming that \({\bf curl}_z({\bf F})(P) = -3\). In which direction would a small paddle placed at \(P\) rotate? How fast would it rotate (in radians per second) if \({\bf F}\) is expressed in meters per second?
Question 17.35
Let \(C_R\) be the circle of radius \(R\) centered at the origin. Use Green’s Theorem to find the value of \(R\) that maximizes \(\displaystyle{\oint_{C_R}\,y^3\,dx + x \, dy}\).
Question 17.36
Area of a Polygon Green’s Theorem leads to a convenient formula for the area of a polygon.
- Let \(C\) be the line segment joining \((x_1,y_1)\) to \((x_2,y_2)\). Show that \[ \frac12\int_C -y\,dx+x\,dy = \frac12(x_1y_2-x_2y_1) \]
- Prove that the area of the polygon with vertices \((x_1,y_1), (x_2, y_2), \dots , (x_n,y_n)\) is equal [where we set \((x_{n+1}, y_{n+1}) = (x_1, y_1)\)] to \[ \frac12\sum_{i=1}^n (x_iy_{i+1}-x_{i+1}y_i) \]
Question 17.37
Use the result of Exercise 32 to compute the areas of the polygons in Figure 17.27. Check your result for the area of the triangle in (A) using geometry.
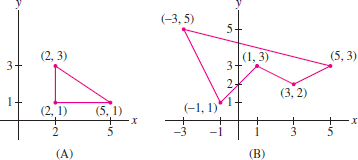
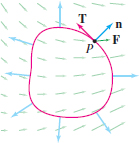
Exercises 34–39: In Section 16.2, we defined the flux of \({\bf F}\) across a curve \(C\) (Figure 17.28) as the integral of the normal component of \({\bf F}\) along \(C\), and we showed that if \({\bf c}(t)=(x(t),y(t))\) is a parametrization of \(C\) for \(a\le t\le b\), then the flux is equal to \[ \int_a^b\,{\bf F}({\bf c}(t))\cdot {\bf n}(t)\,dt \] where \({\bf n}(t)=\langle y'(t),-x'(t)\rangle\).
Question 17.38
Show that the flux of \({\bf F} = \langle P,Q\rangle\) across \(C\) is equal to \(\displaystyle{\oint_C P\,dy - Q\,dx}\).
Question 17.39
Define div\(({\bf F})=\dfrac{\partial{P}}{\partial{x}} + \dfrac{\partial{Q}}{\partial{y}}\). Use Green’s Theorem to prove that for any simple closed curve \(C\), \begin{equation} \textrm{Flux across \(C\)} = \iint_{D\,} div({\bf F})\,dA\tag{12} \end{equation} where \(D\) is the region enclosed by \(C\). This is a two-dimensional version of the Divergence Theorem discussed in Section 17.3.
Question 17.40
Use Eq. (12) to compute the flux of \({\bf F} = \langle 2x+y^3,3y-x^4\rangle\) across the unit circle.
Question 17.41
Use Eq. (12) to compute the flux of \(\displaystyle{{\bf F} = \langle \cos y, \sin y\rangle}\) across the square \(0\le x\le 2\), \(0\le y \le \frac{\pi}2\).
Question 17.42
If \({\bf v}\) is the velocity field of a fluid, the flux of \({\bf v}\) across \(C\) is equal to the flow rate (amount of fluid flowing across \(C\) in m\(^2\)/s). Find the flow rate across the circle of radius \(2\) centered at the origin if \(div({\bf v})=x^2\).
Question 17.43
A buffalo (Figure 17.29) stampede is described by a velocity vector field \({\bf F} = \langle xy - y^3, x^2 + y\rangle\) km/h in the region \(D\) defined by \(2\le x\le 3\), \(2\le y \le 3\) in units of kilometers (Figure 17.30). Assuming a density is \(\rho = 500\) buffalo per square kilometer, use Eq. (12) to determine the net number of buffalo leaving or entering \(D\) per minute (equal to \(\rho\) times the flux of \({\bf F}\) across the boundary of \(D\)).


1015
Further Insights and Challenges
In Exercises 40–43, the Laplace operator \(\Delta\) is defined by \begin{equation} \Delta \varphi = \dfrac{\partial^2\varphi}{\partial x^2} + \dfrac{\partial^2\varphi}{\partial y^2}\tag{13} \end{equation} For any vector field \({\bf F}=\langle F_1, F_2\rangle\), define the conjugate vector field \({\bf F}^* =\langle - F_2, F_1\rangle\).
Question 17.44
Show that if \({\bf F} = \nabla \varphi\), then \({\bf curl}_z({\bf F}^*)=\Delta\varphi\).
Question 17.45
Let \({\bf n}\) be the outward-pointing unit normal vector to a simple closed curve \(C\). The normal derivative of a function \(\varphi\), denoted \(\dfrac{\partial {\varphi}}{\partial{\bf n}}\), is the directional derivative \(D_{{\bf n}}(\varphi) = \nabla\varphi\cdot{\bf n}\). Prove that \[ \oint_C \dfrac{\partial {\varphi}}{\partial{\bf n}}\,ds = \iint_{D\,}\Delta\varphi\,dA \] where \(D\) is the domain enclosed by a simple closed curve \(C\). Hint: Let \({\bf F} = \nabla \varphi\). Show that \(\dfrac{\partial {\varphi}}{\partial{\bf n}} = {\bf F}^*\cdot {\bf T}\) where \({\bf T}\) is the unit tangent vector, and apply Green’s Theorem.
Question 17.46
Let \(P=(a,b)\) and let \(C_r\) be the circle of radius \(r\) centered at \(P\). The average value of a continuous function \(\varphi\) on \(C_r\) is defined as the integral \[ I_\varphi(r) = \frac1{2\pi}\int_0^{2\pi} \varphi(a+r\cos\theta,b+r\sin\theta)\,d\theta \]
- (a) Show that \begin{eqnarray*} &&\dfrac{\partial {\varphi}}{\partial{\bf n}}(a+r\cos\theta,b+r\sin\theta)\\ &&\qquad = \dfrac{\partial {\varphi}}{\partial{\bf r}}(a+r\cos\theta,b+r\sin\theta) \end{eqnarray*}
- (b) Use differentiation under the integral sign to prove that \[ \frac{{d}}{dr} I_\varphi(r) = \frac1{2\pi r}\int_{C_r} \dfrac{\partial {\varphi}}{\partial{\bf n}}\,ds \]
- (c) Use Exercise 41 to conclude that \[ \frac{{d}}{dr}I_\varphi(r) = \frac1{2\pi r}\iint_{D(r)} \Delta\varphi\,dA \] where \(D(r)\) is the interior of \(C_r\).
Question 17.47
Prove that \(m(r)\le I_\varphi(r)\le M(r)\), where \(m(r)\) and \(M(r)\) are the minimum and maximum values of \(\varphi\) on \(C_r\). Then use the continuity of \(\varphi\) to prove that \(\lim\limits_{r\to 0}I_{\varphi}(r)=\varphi(P)\).
In Exercises 44 and 45, let \(D\) be the region bounded by a simple closed curve \(C\). A function \(\varphi(x,y)\) on \(D\) (whose second-order partial derivatives exist and are continuous) is called harmonic if \(\Delta \varphi=0\), where \(\Delta \varphi\) is the Laplace operator defined in Eq. (13).
Question 17.48
Use the results of Exercises 42 and 43 to prove the mean-value property of harmonic functions: If \(\varphi\) is harmonic, then \(I_\varphi(r) = \varphi(P)\) for all \(r\).
Question 17.49
Show that \(f(x,y)=x^2-y^2\) is harmonic. Verify the mean-value property for \(f(x,y)\) directly [expand \(f(a+r\cos\theta,b+r\sin\theta)\) as a function of \(\theta\) and compute \(I_\varphi(r)\)]. Show that \(x^2+y^2\) is not harmonic and does not satisfy the mean-value property.