17.5 Stokes’ Theorem
Stokes’ Theorem is an extension of Green’s Theorem to three dimensions in which circulation is related to a surface integral in \({\bf R}^3\) (rather than to a double integral in the plane). In order to state it, we introduce some definitions and terminology.
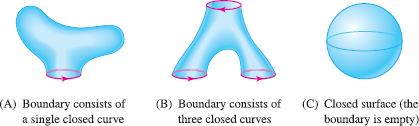
Figure 17.31 shows three surfaces with different types of boundaries. The boundary of a surface is denoted \(\partial S\). Observe that the boundary in (A) is a single, simple closed curve and the boundary in (B) consists of three closed curves. The surface in (C) is called a closed surface because its boundary is empty. In this case, we write \(\partial S = \emptyset\).
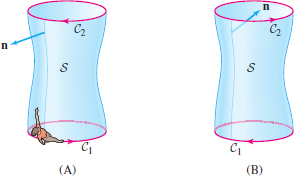
Recall from Section 16.5 that an orientation is a continuously varying choice of unit normal vector at each point of a surface \(S\). When \(S\) is oriented, we can specify an orientation of \(\partial S\), called the boundary orientation. Imagine that you are a unit normal vector walking along the boundary curve. The boundary orientation is the direction for which the surface is on your left as you walk. For example, the boundary of the surface in Figure 17.32 consists of two curves, \(C_1\) and \(C_2\). In (A), the normal vector points to the outside. The woman (representing the normal vector) is walking along \(C_1\) and has the surface to her left, so she is walking in the positive direction. The curve \(C_2\) is oriented in the opposite direction because she would have to walk along \(C_2\) in that direction to keep the surface on her left. The boundary orientations in (B) are reversed because the opposite normal has been selected to orient the surface.
1016
All that’s left is to define curl. The curl of the vector field \({\bf F} = \langle F_1, F_2, F_3\rangle\) is the vector field defined by the symbolic determinant \begin{align*} {\bf curl}({\bf F}) &= \left| \begin{array}{ccc} {\bf i}& {\bf j} & {\bf k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z}\\ F_1 & F_2 & F_3 \end{array} \right| \\ &= \left(\dfrac{\partial{F_3}}{\partial y} - \dfrac{\partial{F_2}}{\partial z}\right){\bf i} - \left(\dfrac{\partial{F_3}}{\partial x} - \dfrac{\partial{F_1}}{\partial z} \right){\bf j} +\left( \dfrac{\partial{F_2}}{\partial{x}} - \dfrac{\partial{F_1}}{\partial{y}}\right){\bf k} \end{align*}
In more compact form, the curl is the symbolic cross product \[ \boxed{ {\bf curl}({\bf F}) = \nabla\times {\bf F}} \] where \(\nabla\) is the del “operator” (also called “nabla”): \[ \nabla= \langle \dfrac{\partial}{\partial{x}} , \dfrac{\partial}{\partial{y}} , \dfrac{\partial}{\partial{z}} \rangle \]
In terms of components, \({\bf curl}({\bf F})\) is the vector field \[ \boxed{ {\bf curl}({\bf F}) = \langle \dfrac{\partial {F_3}}{\partial{y}} - \dfrac{\partial {F_2}}{\partial{z}}, \dfrac{\partial {F_1}}{\partial{z}}-\dfrac{\partial {F_3}}{\partial{x}}, \dfrac{\partial{F_2}}{\partial{x}} - \dfrac{\partial{F_1}}{\partial{y}} \rangle } \]
It is straightforward to check that curl obeys the linearity rules: \begin{align*} {\bf curl}({\bf F}+{\bf G}) &= {\bf curl}({\bf F}) + {\bf curl}({\bf G})\\ {\bf curl}(c{\bf F}) &= c\,{\bf curl}({\bf F})\qquad (\textrm{\(c\) any constant}) \end{align*}
1017
EXAMPLE 1 Calculating the Curl
Calculate the curl of \({\bf F} = \langle xy, e^x,y+z\rangle\).
Solution We compute the curl as a symbolic determinant: \begin{align*} {\bf curl}({\bf F}) &= \left| \begin{array}{ccc} {\bf i}& {\bf j} & {\bf k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ xy & e^x & y+z \\ \end{array} \right| \\ &= \left(\dfrac{\partial}{\partial y}(y+z) - \dfrac{\partial}{\partial{z}}e^x\right){\bf i} - \left(\dfrac{\partial}{\partial{x}}(y+z) - \dfrac{\partial}{\partial{z}} xy \right){\bf j} + \left(\dfrac{\partial}{\partial{x}} e^x - \dfrac{\partial}{\partial{y}} xy \right){\bf k}\\ &= {\bf i} +(e^x-x){\bf k} \end{align*}
EXAMPLE 2 Conservative Vector Fields Have Zero Curl
Verify:
\begin{equation} \boxed{ \textrm{If \({\bf F} = \nabla V\), then \({\bf curl}({\bf F})=0\). That is,\(\quad {\bf curl}(\nabla V)=0\).} }\tag{1} \end{equation}
Solution The curl of a vector field is zero if \[ \dfrac{\partial {F_3}}{\partial{y}} - \dfrac{\partial {F_2}}{\partial{z}} = 0,\qquad \dfrac{\partial {F_1}}{\partial{z}} - \dfrac{\partial {F_3}}{\partial{x}} = 0,\qquad \dfrac{\partial{F_2}}{\partial{x}} - \dfrac{\partial{F_1}}{\partial{y}} = 0 \]
But these equations are equivalent to the cross-partials condition that is satisfied by every conservative vector field \({\bf F} = \nabla V\).
In the next theorem, we assume that \(S\) is an oriented surface with parametrization \(G: D\to S\), where \(D\) is a domain in the plane bounded by smooth, simple closed curves, and \(G\) is one-to-one and regular, except possibly on the boundary of \(D\). More generally, \(S\) may be a finite union of surfaces of this type. The surfaces in applications we consider, such as spheres, cubes, and graphs of functions, satisfy these conditions.
THEOREM 1 Stokes’ Theorem
For surfaces \(S\) as described above, \begin{equation} \boxed{ \oint_{\partial S} {\bf F}\cdot d{\bf s} = \iint_{S\,} {\bf curl}({\bf F})\cdot d{\bf S}}\tag{2} \end{equation}
The integral on the left is defined relative to the boundary orientation of \(\partial S\). If \(S\) is closed (that is, \(\partial S\) is empty), then the surface integral on the right is zero.
Note
The curl measures the extent to which \({\bf F}\) fails to be conservative. If \({\bf F}\) is conservative, then \({\bf curl}({\bf F})={\bf 0}\) and Stokes’ Theorem merely confirms what we already know: The circulation of a conservative vector field around a closed path is zero.
Proof
Each side of Eq. (2) is equal to a sum over the components of \({\bf F}\): \begin{eqnarray*} \oint_C\,{\bf F}\cdot d{\bf s} &=&\oint_C\,F_1\,dx+F_2\,dy+F_3\,dz \\ \iint_{S\,} {\bf curl}({\bf F})\cdot d{\bf S} &=& \iint_{S\,} {\bf curl}(F_1{\bf i})\cdot d{\bf S} + \iint_{S\,} {\bf curl}(F_2{\bf j})\cdot d{\bf S} + \iint_{S\,} {\bf curl}(F_3{\bf k})\cdot d{\bf S} \end{eqnarray*}
The proof consists of showing that the \(F_1\)-, \(F_2\)-, and \(F_3\)-terms are separately equal.
Because a complete proof is quite technical, we will prove it under the simplifying assumption that \(S\) is the graph of a function \(z = f(x,y)\) lying over a domain \(D\) in the \(xy\)-plane. Furthermore, we will carry the details only for the \(F_1\)-terms. The calculation for \(F_2\)-components is similar, and we leave as an exercise the equality of the \(F_3\)-terms (Exercise 31). Thus, we shall prove that \begin{equation} \oint_C\,F_1\,dx = \iint_{S\,} {\bf curl}(F_1(x,y,z){\bf i})\cdot d{\bf S}\tag{3} \end{equation}
1018
Orient \(S\) with upward-pointing normal as in Figure 17.33 and let \(C=\partial S\) be the boundary curve. Let \(C_0\) be the boundary of \(D\) in the \(xy\)-plane, and let \({\bf c}_0(t)= (x(t), y(t))\) (for \(a\le t\le b\)) be a counterclockwise parametrization of \(C_0\) as in Figure 17.33. The boundary curve \(C\) projects onto \(C_0\), so \(C\) has parametrization \begin{align*} {\bf c}(t) &= \bigl( x(t), y(t), f(x(t),y(t)) \bigr) \end{align*} and thus \begin{align*} \oint_C F_1(x,y,z) \, dx &= \int_a^b F_1\bigl(x(t),y(t),f(x(t),y(t))\bigr)\frac{{dx}}{dt}\,dt \end{align*}
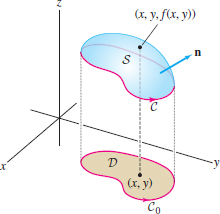
The integral on the right is precisely the integral we obtain by integrating \(F_1\bigl(x,y,f(x,y)\bigr)\,dx\) over the curve \(C_0\) in the plane \({\bf R}^2\). In other words, \[ \oint_C F_1(x,y,z)\,dx = \int_{C_0} F_1\bigl(x,y,f(x,y)\bigr)\,dx \]
By Green’s Theorem applied to the integral on the right, \[ \oint_C F_1(x,y,z)\, dx = - \iint_{D\,}\dfrac{\partial}{\partial{y}} F_1(x,y,f(x,y)) \,dA \]
By the Chain Rule, \[ \dfrac{\partial}{\partial{y}} F_1\big(x,y,f(x,y)\big) = F_{1y}\big(x,y,f(x,y)\big)+F_{1z}\big(x,y,f(x,y)\big)f_y(x,y) \] so finally we obtain \begin{equation} \oint_C F_1\,dx = - \iint_{D\,} \Big(F_{1y}\big(x,y,f(x,y)\big)+F_{1z}\big(x,y,f(x,y)\big)f_y(x,y)\Big)\,dA\tag{4} \end{equation}
REMINDER
Calculating a surface integral: \begin{align*} \iint_S\,{\bf F}\cdot\,d{\bf S} &= \iint_D\,{\bf F}(u,v)\cdot {\bf n}(u,v)\,du\,dv \end{align*}
If \(S\) is a graph \(z=f(x,y)\), parametrized by \(G(x,y)=(x,y,f(x,y))\), then \({\bf n}(x,y) =\langle-f_x(x,y), -f_y(x,y), 1\rangle\)
To finish the proof, we compute the surface integral of \({\bf curl}({\bf F}_1{\bf i})\) using the parametrization \(G(x,y)=(x,y,f(x,y))\) of \(S\): \begin{eqnarray} {\bf n} &=& \langle-f_x(x,y), -f_y(x,y), 1\rangle\qquad\textrm{(upward-pointing normal)}\notag\\ {\bf curl}(F_1{\bf i})\cdot{\bf n} &=& \langle 0, F_{1z}, -F_{1y}\rangle\cdot\langle-f_x(x,y), -f_y(x,y), 1\rangle\notag\\ &=& -F_{1z}\big(x,y,f(x,y)\big)f_y(x,y)-F_{1y}\big(x,y,f(x,y)\big)\notag\\ \iint_{S\,} {\bf curl}(F_1{\bf i})\cdot d{\bf S} &=& - \iint_{D\,}\notag \Big(F_{1z}(x,y,z)f_y(x,y)+F_{1y}\big(x,y,f(x,y)\big)\Big)\,dA\tag{5} \end{eqnarray}
The right-hand sides of Eq. (4) and Eq. (5) are equal. This proves Eq. (3).
EXAMPLE 3 Verifying Stokes’ Theorem
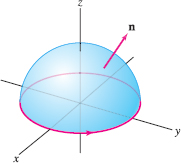
Verify Stokes’ Theorem for \[ {\bf F} = \langle -y, 2x, x+z\rangle \] and the upper hemisphere with outward-pointing normal vectors (Figure 17.34): \[ S=\{(x,y,z): x^2+y^2+z^2=1, z\ge 0\} \]
1019
Solution We will show that both the line integral and the surface integral in Stokes’ Theorem are equal to \(3\pi\).
REMINDER
In Eq. (6), we use \[ \int_0^{2\pi} \cos^2t\,dt=\int_0^{2\pi}\frac{1+\cos 2t}2\,dt=\pi \]
Step 1. Compute the line integral around the boundary curve.
The boundary of \(S\) is the unit circle oriented in the counterclockwise direction with parametrization \({\bf c}(t)=(\cos t, \sin t, 0)\). Thus, \begin{align} {\bf c}'(t) &= \langle-\sin t, \cos t, 0\rangle\notag\\ {\bf F}({\bf c}(t)) &= \langle -\sin t, 2\cos t, \cos t\rangle\notag\\ {\bf F}({\bf c}(t))\cdot{\bf c}'(t) &=\langle -\sin t, 2\cos t, \cos t\rangle\cdot\langle-\sin t, \cos t, 0\rangle\notag\\ & = \sin^2t+2\cos^2t=1+\cos^2t\notag\\ \oint_{\partial S} {\bf F}\cdot d{\bf s} &= \int_0^{2\pi}(1+\cos^2t)\,dt = 2\pi +\pi= \boxed{3\pi}\tag{6} \end{align}
Step 2. Compute the curl.
\begin{eqnarray*} {\bf curl}({\bf F}) &=& \left| \begin{array}{ccc} {\bf i}& {\bf j} & {\bf k} \\ \displaystyle\dfrac{\partial}{\partial{x}} & \displaystyle\dfrac{\partial}{\partial{y}} & \displaystyle\dfrac{\partial}{\partial{z}} \\ -y & 2x & x+z \\ \end{array} \right| \\ &=& \left(\dfrac{\partial}{\partial{y}}(x+z) - \dfrac{\partial}{\partial{z}} 2x\right){\bf i} - \left(\dfrac{\partial}{\partial{x}}(x+z) - \dfrac{\partial}{\partial{z}}(-y)\right){\bf j} \\ &&{} + \left(\dfrac{\partial}{\partial{x}}\,2x - \dfrac{\partial}{\partial{y}}\, (-y)\right){\bf k} \\ &=& \langle 0, -1,3\rangle \end{eqnarray*}
REMINDER
Stokes’ Theorem states \[ \oint_{\partial S} {\bf F}\cdot d{\bf s} = \iint_{S\,} {\bf curl}({\bf F})\cdot d{\bf S} \]
Step 3. Compute the surface integral of the curl.
We parametrize the hemisphere using spherical coordinates: \[ G(\theta,\phi)=(\cos\theta\sin\phi,\sin\theta\sin\phi,\cos\phi) \]
By Eq. (2) of Section 16.4, the outward-pointing normal vector is \[ {\bf n} = \sin\phi\langle \cos\theta\sin\phi,\sin\theta\sin\phi,\cos\phi\rangle \]
Therefore, \begin{align*} {\bf curl}({\bf F})\cdot {\bf n} &= \sin\phi\langle 0, -1, 3\rangle\cdot \langle \cos\theta\sin\phi,\sin\theta\sin\phi,\cos\phi\rangle\\ &= -\sin\theta\sin^2\phi + 3\cos\phi\sin\phi \end{align*}
The upper hemisphere \(S\) corresponds to \(0\le \phi\le\frac{\pi}2\), so \begin{align*} \iint_{S\,} {\bf curl}({\bf F})\cdot d{\bf S} &= \int_{\phi=0}^{\pi/2}\int_{\theta=0}^{2\pi} (-\sin\theta\sin^2\phi + 3\cos\phi\sin\phi)\,d\theta\,d\phi\\ &= 0+2\pi\int_{\phi=0}^{\pi/2} 3\cos\phi\sin\phi \,d\phi = 2\pi\left(\frac32\sin^2\phi\right)\bigg|_{\phi=0}^{\pi/2}\\ &= \boxed{3\pi} \end{align*}
1020
Notice that \({\bf curl}({\bf F})\) contains the partial derivatives \(\displaystyle{\dfrac{\partial{F_1}}{\partial{y}}}\) and \(\displaystyle{\dfrac{\partial {F_1}}{\partial{z}}}\) but not the partial \(\displaystyle{\dfrac{\partial{F_1}}{\partial{x}}}\). So if \(F_1=F_1(x)\) is a function of \(x\) alone, then \(\displaystyle{\dfrac{\partial{F_1}}{\partial{y}}=\dfrac{\partial {F_1}}{\partial{z}}=0}\), and \(F_1\) does not contribute to the curl. The same holds for the other components. In summary, if each of \(F_1\), \(F_2\), and \(F_3\) depends only on its corresponding variable \(x\), \(y\), or \(z\), then \[ {\bf curl}\bigl(\langle F_1(x), F_2(y), F_3(z) \rangle\bigr) = 0 \]
EXAMPLE 4
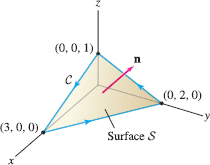
Use Stokes’ Theorem to show that \(\displaystyle{\oint_C {\bf F}\cdot d{\bf s} = 0}\), where \[ {\bf F} = \langle \sin(x^2), e^{y^2}+ x^2, z^4+2x^2\rangle \] and \(C\) is the boundary of the triangle in Figure 17.35 with the indicated orientation.
Solution We apply Stokes’ Theorem \[ \oint_C {\bf F}\cdot d{\bf s} = \iint_{S\,} {\bf curl}({\bf F})\cdot \,d{\bf S} \] and show that the integral on the right is zero.
By the preceding remark, the first component \(\sin(x^2)\) does not contribute to the curl since it depends only on \(x\). Similarly, \(e^{y^2}\) and \(z^4\) drop out of the curl, and we have \begin{align*} {\bf curl}\Bigl(\langle \sin x^2, e^{y^2} + x^2, z^4+2x^2\rangle\Bigr) \quad& = \quad \overbrace{{\bf curl}\Bigl(\langle \sin x^2,e^{y^2},z^4 \rangle\Bigr)}^{\textrm{Automatically zero}} {}+ {\bf curl}\Bigl(\langle 0,x^2,2x^2 \rangle\Bigr) \\ &= \langle 0,-\dfrac{\partial}{\partial{x}} 2x^2,\dfrac{\partial}{\partial{x}} x^2 \rangle = \langle 0,-4x,2x \rangle \end{align*}
Now, it turns out (by the author’s design) that we can show the surface integral is zero without actually computing it. Referring to Figure 17.35, we see that \(C\) is the boundary of the triangular surface \(S\) contained in the plane \[ \frac{x}3+\frac{y}2+z=1 \]
Therefore, \({{\bf u} = \big\langle\frac13, \frac12,1\big\rangle}\) is a normal vector to this plane. But \({\bf u}\) and \({\bf curl}({\bf F})\) are orthogonal: \[ {\bf curl}({\bf F})\cdot{\bf u} = \langle 0, - 4x, 2x\rangle \cdot \langle \frac13, \frac12,1\rangle = -2x+2x = 0 \]
In other words, the normal component of \({\bf curl}({\bf F})\) along \(S\) is zero. Since the surface integral of a vector field is equal to the surface integral of the normal component, we conclude that \(\displaystyle{ \iint_{S\,} {\bf curl}({\bf F})\cdot \,d{\bf S} = 0}\).
1021
CONCEPTUAL INSIGHT
Recall that if \({\bf F}\) is conservative—that is, \({\bf F} = \nabla V\)—then for any two paths \(C_1\) and \(C_2\) from \(P\) to \(Q\) (Figure 17.36), \[ \int_{C_1} {\bf F} \cdot d{\bf s} = \int_{C_2} {\bf F} \cdot d{\bf s} = V(Q)- V(P) \]
In other words, the line integral is path independent. In particular, \(\displaystyle{\oint_{C} {\bf F} \cdot d{\bf s}}\) is zero if \(C\) is closed (\(P=Q\)).
Analogous facts are true for surface integrals when \({\bf F}={\bf curl}({\bf A})\). The vector field \({\bf A}\) is called a vector potential for \({\bf F}\). Stokes’ Theorem tells us that for any two surfaces \(S_1\) and \(S_2\) with the same oriented boundary \(C\) (Figure 17.37), \[ \iint_{S_1\,}{\bf F}\cdot d{\bf S} = \iint_{S_2\,}{\bf F}\cdot d{\bf S} = \oint_{C}{\bf A}\cdot d{\bf s} \]
In other words, the surface integral of a vector field with vector potential \({\bf A}\) is surface independent, just as a vector field with a potential function \(V\) is path independent.
If the surface is closed, then the boundary curve is empty and the surface integral is zero: \[ \iint_{S\,}{\bf F}\cdot d{\bf S}=0\qquad\textrm{if}\quad \textrm{\({\bf F}={\bf curl}({\bf A})\) and \(S\) is closed} \]

Note
Vector potentials are not unique: If \({\bf F}={\bf curl}({\bf A})\), then \({\bf F}={\bf curl}({\bf A}+{\bf B})\) for any vector field \({\bf B}\) such that \({\bf curl}({\bf B})={\bf 0}\).
THEOREM 2 Surface Independence for Curl Vector Fields
If \({\bf F} = {\bf curl}({\bf A})\), then the flux of \({\bf F}\) through a surface \(S\) depends only on the oriented boundary \(\partial S\) and not on the surface itself: \begin{equation} \iint_{S\,} {\bf F} \cdot d{\bf S} = \oint_{\partial S} {\bf A} \cdot d{\bf s}\tag{7} \end{equation}
In particular, if \(S\) is closed (that is, \(\partial S\) is empty), then \(\displaystyle{ \iint_{S\,} {\bf F}\cdot d{\bf S} = 0}\).
EXAMPLE 5
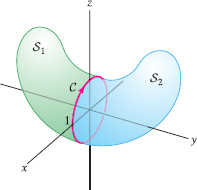
Let \({\bf F} = {\bf curl}({\bf A})\), where \({\bf A} = \langle y+z,\sin(xy),e^{xyz}\rangle\). Find the flux of \({\bf F}\) through the surfaces \(S_1\) and \(S_2\) in Figure 17.38 whose common boundary \(C\) is the unit circle in the \(xz\)-plane.
REMINDER
By the flux of a vector field through a surface, we mean the surface integral of the vector field.
Solution With \(C\) oriented in the direction of the arrow, \(S_1\) lies to the left, and by Eq. (7), \[ \iint_{S_1\,} {\bf F}\cdot d{\bf S} = \oint_C {\bf A}\cdot d{\bf s} \]
We shall compute the line integral on the right. The parametrization \({\bf c}(t)=(\cos t, 0, \sin t)\) traces \(C\) in the direction of the arrow because it begins at \({\bf c}(0)=(1,0,0)\) and moves in the direction of \({\bf c}\big(\frac{\pi}2\big)=(0,0,1)\). We have \begin{align*} {\bf A}({\bf c}(t))&= \langle 0 + \sin t, \sin(0), e^0\rangle = \langle \sin t, 0, 1\rangle \\ {\bf A}({\bf c}(t))\cdot {\bf c}'(t)&= \langle \sin t, 0, 1\rangle \cdot \langle -\sin t, 0, \cos t\rangle =-\sin^2t+\cos t\\ \oint_C {\bf A}\cdot d{\bf s} &= \int_0^{2\pi} (-\sin^2t+\cos t)\,dt =-\pi \end{align*}
1022
We conclude that \(\displaystyle{\iint_{S_1\,} {\bf F}\cdot d{\bf S}=-\pi}\). On the other hand, \(S_2\) lies on the right as you traverse \(C\). Therefore \(S_2\) has oriented boundary \(-C\), and \[ \iint_{S_2\,} {\bf F}\cdot d{\bf S}= \oint_{-C} {\bf A}\cdot d{\bf s}=-\oint_C {\bf A}\cdot d{\bf s} = \pi \]
CONCEPTUAL INSIGHT Interpretation of the Curl
In Section 17.1, we showed that the quantity \(\displaystyle{\dfrac{\partial{F_2}}{\partial{x}}-\dfrac{\partial{F_1}}{\partial{y}}}\) in Green’s Theorem is the “circulation per unit of enclosed area.” A similar interpretation is valid in \({\bf R}^3\).
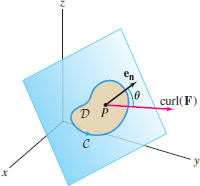
Consider a plane through a point \(P\) with unit normal vector \({\bf e}_{\bf n}\) and let \(D\) be a small domain containing \(P\) with boundary curve \(C\) (Figure 17.39). By Stokes’ Theorem, \begin{equation} \oint_{C}{\bf F}\cdot\,d{\bf s} \approx \iint_{D}({\bf curl}({\bf F})\cdot{\bf e}_{\bf n}) \, dS\tag{8} \end{equation}
The vector field \(\displaystyle{{\bf curl}({\bf F})}\) is continuous (its components are derivatives of the components of \({\bf F}\)), so its value does not change much on \(D\) if \(D\) is sufficiently small. To a first approximation, we can replace \({\bf curl}({\bf F})\) by the constant value \({\bf curl}({\bf F})(P)\), giving us the approximation \begin{align} \iint_{D}({\bf curl}({\bf F})\cdot{\bf e}_{\bf n}) \, dS &\approx \iint_{D}({\bf curl}({\bf F})(P)\cdot{\bf e}_{\bf n}) \, dS\notag\\ &\approx ({\bf curl}({\bf F})(P)\cdot{\bf e}_{\bf n}) \, \textrm{Area}(D)\tag{9} \end{align}
Furthermore, \(\displaystyle{{\bf curl}({\bf F})(P)\cdot{\bf e}_{\bf n} = \|{{\bf curl}({\bf F})(P)}\|\cos\theta}\), where \(\theta\) is the angle between \({\bf curl}({\bf F})\) and \({\bf e}_{\bf n}\). Together, Eq. (8) and Eq. (9) give us \begin{equation} \oint_{C}{\bf F}\cdot\,d{\bf s} \approx \|{{\bf curl}({\bf F})(P)}\|(\cos\theta) \, \textrm{Area}(D)\tag{10} \end{equation}
This is a remarkable result. It tells us that \({\bf curl}({\bf F})\) encodes the the circulation per unit of enclosed area in every plane through \(P\) in a simple way—namely, as the dot product \(\displaystyle{{\bf curl}({\bf F})(P)\cdot{\bf e}_{\bf n}}\). In particular, the circulation rate varies (to a first-order approximation) as the cosine of the angle \(\theta\) between \({\bf curl}({\bf F})(P)\) and \({\bf e}_{\bf n}\).
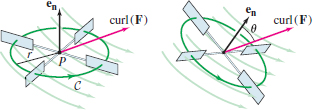
We can also argue (as in Section 17.1 for vector fields in the plane) that if \({\bf F}\) is the velocity field of a fluid, then a small paddle wheel with normal \({\bf e}_{\bf n}\) will rotate with an angular velocity of approximately \({\frac12{\bf curl}({\bf F})(P)\cdot{\bf e}_{\bf n}}\) (see Figure 17.40).
EXAMPLE 6 Vector Potential for a Solenoid
An electric current flowing through a solenoid (a tightly wound spiral of wire; see Figure 17.41) creates a magnetic field \({\bf B}\). If we assume that the solenoid is infinitely long, with radius \(R\) and the \(z\)-axis as central axis, then \[ {\bf B} = \begin{cases} {\bf 0} & \textrm{if \(r > R\)} \\ B{\bf k} &\textrm{if \(r<R\)} \end{cases} \]
1023
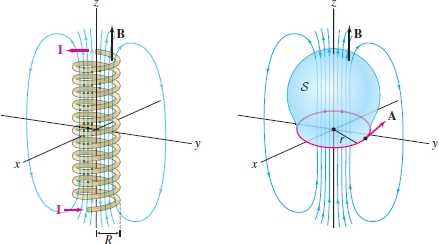
where \(r = (x^2+y^2)^{1/2}\) and \(B\) is a constant that depends on the current strength and the spacing of the turns of wire.
- (a) Show that a vector potential for \({\bf B}\) is \[ {\bf A} = \begin{cases} \dfrac12 R^2 B\langle -\dfrac{y}{r^2}, \dfrac{x}{r^2}, 0\rangle & \textrm{if \(r> R\)} \\ \dfrac12B\langle -y, x, 0\rangle &\textrm{if \(r<R\)} \end{cases} \]
- (b) Calculate the flux of \({\bf B}\) through the surface \(S\) (with upward-pointing normal) in Figure 17.41 whose boundary is a circle of radius \(r\) where \(r>R\).
Solution
- (a) For any functions \(f\) and \(g\), \[ {\bf curl}(\langle f, g, 0 \rangle) = \langle -g_z, f_z, g_x-f_y\rangle \] Applying this to \({\bf A}\) for \(r<R\), we obtain \[ {\bf curl}({\bf A}) = \frac1{2}B\langle 0,0, \dfrac{\partial{}}{\partial{x}} x - \dfrac{\partial{}}{\partial{y}}(-y )\rangle = \langle 0,0,B\rangle = B{\bf k} = {\bf B} \] We leave it as an exercise [Exercise 29] to show that \({\bf curl}({\bf A}) ={\bf B}={\bf 0}\) for \(r>R\).
- (b) The boundary circle of \(S\) with counterclockwise parametrization \({\bf c}(t)=(r\cos t,r\sin t, 0)\), so \begin{align*} {\bf c}'(t) &= \langle -r\sin t, r\cos t, 0\rangle\\ {\bf A}({\bf c}(t))&=\frac12R^2Br^{-1}\langle -\sin t, \cos t, 0\rangle \\ {\bf A}({\bf c}(t))\cdot {\bf c}'(t) &=\frac12R^2B \left((-\sin t)^2+\cos^2t \right) = \frac12R^2B \end{align*}
Note
The vector potential \({\bf A}\) is continuous but not differentiable on the cylinder \(r=R\), that is, on the solenoid itself (Figure 17.42). The magnetic field \({\bf B}={\bf curl}({\bf A})\) has a jump discontinuity where \(r=R\). We take for granted the fact that Stokes’ Theorem remains valid in this setting.

By Stokes’ Theorem, the flux of \({\bf B}\) through \(S\) is equal to \begin{align*} \iint_{S\,}{\bf B}\cdot d{\bf S} &= \oint_{\partial S}{\bf A}\cdot d{\bf s} = \int_0^{2\pi} {\bf A}({\bf c}(t))\cdot {\bf c}'(t)\,dt = \frac12R^2B \int_0^{2\pi} dt =\pi R^2B \end{align*}
CONCEPTUAL INSIGHT
There is an interesting difference between scalar and vector potentials. If \({\bf F}=\nabla V\), then the scalar potential \( V\) is constant in regions where the field \({\bf F}\) is zero (since a function with zero gradient is constant). This is not true for vector potentials. As we saw in Example 6, the magnetic field \({\bf B}\) produced by a solenoid is zero everywhere outside the solenoid, but the vector potential \({\bf A}\) is not constant outside the solenoid. In fact, \({\bf A}\) is proportional to \(\displaystyle{\langle -\dfrac{y}{r^2},\dfrac{x}{r^2},0\rangle}\). This is related to an intriguing phenomenon in physics called the Aharonov-Bohm (AB) effect, first proposed on theoretical grounds in the 1940s.
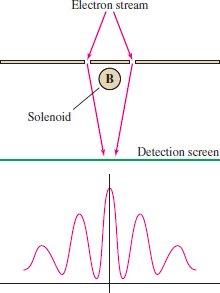
According to electromagnetic theory, a magnetic field \({\bf B}\) exerts a force on a moving electron, causing a deflection in the electron’s path. We do not expect any deflection when an electron moves past a solenoid because \({\bf B}\) is zero outside the solenoid (in practice, the field is not actually zero, but it is very small—we ignore this difficulty). However, according to quantum mechanics, electrons have both particle and wave properties. In a double-slit experiment, a stream of electrons passing through two small slits creates a wavelike interference pattern on a detection screen (Figure 17.43). The AB effect predicts that if we place a small solenoid between the slits as in the figure (the solenoid is so small that the electrons never pass through it), then the interference pattern will shift slightly. It is as if the electrons are “aware” of the magnetic field inside the solenoid, even though they never encounter the field directly.
The AB effect was hotly debated until it was confirmed definitively in 1985, in experiments carried out by a team of Japanese physicists led by Akira Tonomura. The AB effect appeared to contradict “classical” electromagnetic theory, according to which the trajectory of an electron is determined by \({\bf B}\) alone. There is no such contradiction in quantum mechanics, because the behavior of the electrons is governed not by \({\bf B}\) but by a “wave function” derived from the nonconstant vector potential \({\bf A}\).