Question 17.50

Indicate with an arrow the boundary orientation of the boundary curves of the surfaces in Figure 17.44, oriented by the outward-pointing normal vectors.

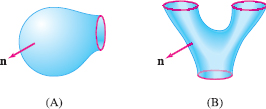
Question 17.51

Let \({\bf F} = {\bf curl}({\bf A})\). Which of the following are related by Stokes’ Theorem?

• (a) The circulation of \({\bf A}\) and flux of \({\bf F}\).
• (b) The circulation of \({\bf F}\) and flux of \({\bf A}\).

Question 17.52

What is the definition of a vector potential?

Question 17.53

Which of the following statements is correct?

• (a) The flux of \({\bf curl}({\bf A})\) through every oriented surface is zero.
• (b) The flux of \({\bf curl}({\bf A})\) through every closed, oriented surface is zero.

Question 17.54

Which condition on \({\bf F}\) guarantees that the flux through \(S_1\) is equal to the flux through \(S_2\) for any two oriented surfaces \(S_1\) and \(S_2\) with the same oriented boundary?

Question 17.55

\({\bf F}=\langle z - y^2, x + z^3, y + x^2\rangle\)

Question 17.56

\(\displaystyle{{\bf F}=\langle \frac{y}x, \frac{y}z, \frac{z}x \rangle}\)

Question 17.57

\({\bf F}=\langle e^y,\sin x, \cos x\rangle\)

Question 17.58

\(\displaystyle{{\bf F}=\langle \frac{x}{x^2+y^2}, \frac{y}{x^2+y^2},0 \rangle}\)

Question 17.59

\({\bf F}=\langle 2xy, x, y+z\rangle,\quad\) the surface \(z=1-x^2-y^2\) for \(x^2+ y^2\le 1\)

Question 17.60

\({\bf F} = \langle y z,0,x\rangle,\quad\) the portion of the plane \(\displaystyle{\frac{x}2 +\frac{y}3+z=1}\) where \(x, y, z \ge 0 \)

Question 17.61

\({\bf F} = \langle e^{y-z}, 0,0\rangle,\quad\) the square with vertices \((1,0,1)\), \((1,1,1)\), \((0,1,1)\), and \((0,0,1)\)

Question 17.62

\({\bf F} = \langle y, x, x^2+y^2\rangle,\quad\) the upper hemisphere \(x^2+y^2+z^2=1\), \(z\ge 0\)

Question 17.63

\({\bf F} = \langle e^{z^2}-y,e^{z^3}+x,\cos(xz)\rangle,\quad\) the upper hemisphere \(x^2+y^2+z^2=1\), \(z\ge 0\) with outward-pointing normal

Question 17.64

\({\bf F} = \langle x+y,z^2-4,x\sqrt{y^2+1})\rangle,\quad\) surface of the wedge-shaped box in Figure 17.45 (bottom included, top excluded) with outward-point-ing normal

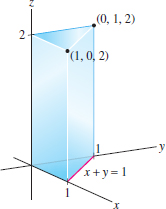
Question 17.65

Let \(S\) be the surface of the cylinder (not including the top and bottom) of radius 2 for \(1\le z \le 6\), oriented with outward-pointing normal (Figure 17.46).

• (a) Indicate with an arrow the orientation of \(\partial S\) (the top and bottom circles).
• (b) Verify Stokes’ Theorem for \(S\) and \({\bf F} = \langle yz^2, 0, 0\rangle\).

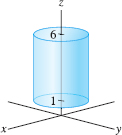
Question 17.66

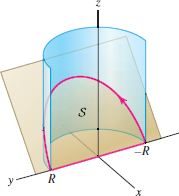
Let \(S\) be the portion of the plane \(z=x\) contained in the half-cylinder of radius \(R\) depicted in Figure 17.47. Use Stokes’ Theorem to calculate the circulation of \({\bf F}=\langle z, x, y + 2z\rangle\) around the boundary of \(S\) (a half-ellipse) in the counterclockwise direction when viewed from above. Hint: Show that \({\bf curl}({\bf F})\) is orthogonal to the normal vector to the plane.

Question 17.67

Let \(I\) be the flux of \({\bf F} = \langle e^y,2xe^{x^2}, z^2 \rangle\) through the upper hemisphere \(S\) of the unit sphere.

• (a) Let \({\bf G} = \langle e^y, 2xe^{x^2},0\rangle\). Find a vector field \({\bf A}\) such that \({\bf curl}({\bf A})= {\bf G}\).
• (b) Use Stokes’ Theorem to show that the flux of \({\bf G}\) through \(S\) is zero. Hint: Calculate the circulation of \({\bf A}\) around \(\partial S\).
• (c) Calculate \(I\). Hint: Use (b) to show that \(I\) is equal to the flux of \(\langle 0,0,z^2\rangle\) through \(S\).

Question 17.68

Let \({\bf F} = \langle 0, -z, 1\rangle\). Let \(S\) be the spherical cap \(x^2+y^2+z^2\le 1\), where \(z\ge\tfrac12\). Evaluate \(\displaystyle{\iint_{S\,} {\bf F}\cdot d{\bf S}}\) directly as a surface integral. Then verify that \({\bf F}={\bf curl}({\bf A})\), where \({\bf A}=(0,x,xz)\) and evaluate the surface integral again using Stokes’ Theorem.

Question 17.69

Let \({\bf A}\) be the vector potential and \({\bf B}\) the magnetic field of the infinite solenoid of radius \(R\) in Example 6. Use Stokes’ Theorem to compute:

• (a) The flux of \({\bf B}\) through a circle in the \(xy\)-plane of radius \(r<R\)
• (b) The circulation of \({\bf A}\) around the boundary \(C\) of a surface lying outside the solenoid

Question 17.70

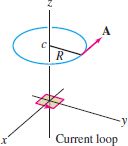
The magnetic field \({\bf B}\) due to a small current loop (which we place at the origin) is called a magnetic dipole (Figure 17.48). Let \(\rho=(x^2+y^2+z^2)^{1/2}\). For \(\rho\) large, \({\bf B}={\bf curl}({\bf A})\), where \[ {\bf A}=\langle -\frac{y}{\rho^3}, \frac{x}{\rho^3},0\rangle \]

• (a) Let \(C\) be a horizontal circle of radius \(R\) with center \((0,0,c)\), where \(c\) is large. Show that \({\bf A}\) is tangent to \(C\).
• (b) Use Stokes’ Theorem to calculate the flux of \({\bf B}\) through \(C\).

Question 17.71

A uniform magnetic field \({\bf B}\) has constant strength \(b\) in the \(z\)-direction [that is, \({\bf B} = \langle 0,0,b\rangle\)].

• (a) Verify that \({\bf A}=\frac12{\bf B}\times {\bf r}\) is a vector potential for \({\bf B}\), where \({\bf r} = \langle x,y,0\rangle\).
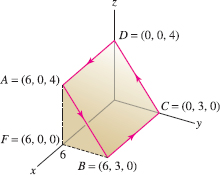
• (b) Calculate the flux of \({\bf B}\) through the rectangle with vertices \(A\), \(B\), \(C\), and \(D\) in Figure 17.49.

Question 17.72

Let \({\bf F} = \langle -x^2y, x, 0\rangle\). Referring to Figure 17.49, let \(C\) be the closed path \(ABCD\). Use Stokes’ Theorem to evaluate \(\displaystyle{\int_{C}{\bf F}\cdot d{\bf s}}\) in two ways. First, regard \(C\) as the boundary of the rectangle with vertices \(A\), \(B\), \(C\), and \(D\). Then treat \(C\) as the boundary of the wedge-shaped box with open top.

Question 17.73

Let \({\bf F} = \langle y^2, 2z + x, 2y^2 \rangle\). Use Stokes’ Theorem to find a plane with equation \(\displaystyle{ax+by+cz=0}\) (where \(a,b,c\) are not all zero) such that \(\displaystyle{\oint_C\,{\bf F}\cdot\,d{\bf s}=0}\) for every closed \(C\) lying in the plane. Hint: Choose \(a,b,c\) so that \({\bf curl}({\bf F})\) lies in the plane.

Question 17.74

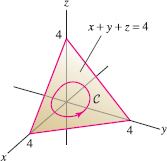
Let \({\bf F}=\langle -z^2, 2zx, 4y - x^2\rangle\) and let \(C\) be a simple closed curve in the plane \(x+y+z=4\) that encloses a region of area \(16\) (Figure 17.50). Calculate \(\displaystyle{\oint_C{\bf F}\cdot d{\bf s}}\), where \(C\) is oriented in the counterclockwise direction (when viewed from above the plane).

Question 17.75

Let \({\bf F} = \langle y^2, x^2, z^2\rangle\). Show that \[ \int_{C_1} {\bf F} \cdot d{\bf s} = \int_{C_2} {\bf F} \cdot d{\bf s} \] for any two closed curves lying on a cylinder whose central axis is the \(z\)-axis (Figure 17.51).

Question 17.76

The curl of a vector field \({\bf F}\) at the origin is \({\bf v}_0 = \langle 3,1,4\rangle\). Estimate the circulation around the small parallelogram spanned by the vectors \({\bf A}=\langle 0,\tfrac12,\tfrac12\rangle\) and \({\bf B}=\langle 0,0,\tfrac13\rangle\).

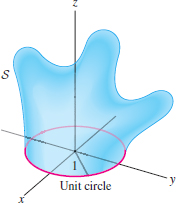
Question 17.77

You know two things about a vector field \({\bf F}\):

• (i) \({\bf F}\) has a vector potential \({\bf A}\) (but \({\bf A}\) is unknown).
• (ii) The circulation of \({\bf A}\) around the unit circle (oriented counterclockwise) is 25.

Determine the flux of \({\bf F}\) through the surface \(S\) in Figure 17.52, oriented with upward pointing normal.

Figure 17.52: Surface \(S\) whose boundary is the unit circle.

Question 17.78

Suppose that \({\bf F}\) has a vector potential and that \({\bf F}(x, y, 0) = {\bf k}\). Find the flux of \({\bf F}\) through the surface \(S\) in Figure 17.38, oriented with upward pointing normal.

Question 17.79

Prove that \(\displaystyle{{\bf curl}(f{\bf A}) = \nabla f\times{\bf A}}\), where \(f\) is a differentiable function and \({\bf A}\) is a constant vector.

Question 17.80

Show that \({\bf curl}({\bf F})=\mathbf{0}\) if \({\bf F}\) is radial, meaning that \({\bf F}=f(\rho)\langle x, y, z\rangle\) for some function \(f(\rho)\), where \(\rho=\sqrt{x^2+y^2+z^2}\). Hint: It is enough to show that one component of \({\bf curl}({\bf F})\) is zero, because it will then follow for the other two components by symmetry.

Question 17.81

Prove the following Product Rule: \begin{equation*} {\bf curl}(f{\bf F}) = f{\bf curl}({\bf F}) + \nabla f\times{\bf F} \end{equation*}

Question 17.82

Assume that \(f\) and \(g\) have continuous partial derivatives of order 2. Prove that \[ \oint_{\partial S} f\nabla(g)\cdot d{\bf s} = \iint_{S} \nabla(f)\times\nabla(g)\cdot d{\bf s} \]

Question 17.83

Verify that \({\bf B}={\bf curl}({\bf A})\) for \(r>R\) in the setting of Example 6.

Question 17.84

Explain carefully why Green’s Theorem is a special case of Stokes’ Theorem.

Question 17.85

In this exercise, we use the notation of the proof of Theorem 1 and prove \begin{equation} \oint_C F_3(x,y,z){\bf k} \cdot d{\bf s} = \iint_{S} {\bf curl}(F_3(x,y,z){\bf k})\cdot d{\bf S}\tag{11} \end{equation}

In particular, \(S\) is the graph of \(z=f(x,y)\) over a domain \(D\), and \(C\) is the boundary of \(S\) with parametrization \((x(t),y(t),f(x(t),y(t)))\).

• (a) Use the Chain Rule to show that \begin{multline*} F_3(x,y,z){\bf k}\cdot d{\bf s} =F_3(x(t),y(t),f(x(t),y(t))\\ \Big(f_x(x(t),y(t))x'(t)+f_y(x(t),y(t))y'(t)\Big)\,dt \end{multline*} and verify that \begin{multline*} \oint_C F_3(x,y,z){\bf k}\cdot d{\bf s} =\\ \oint_{C_0} \langle F_3(x,y,z)f_x(x,y),F_3(x,y,z) f_y(x,y)\rangle\cdot d{\bf s} \end{multline*} where \(C_0\) has parametrization \((x(t),y(t))\).
• (b) Apply Green’s Theorem to the line integral over \(C_0\) and show that the result is equal to the right-hand side of Eq. (11).

Question 17.86

Let \({\bf F}\) be a continuously differentiable vector field in \({\bf R}^3\), \(Q\) a point, and \(S\) a plane containing \(Q\) with unit normal vector \({\bf e}\). Let \(C_r\) be a circle of radius \(r\) centered at \(Q\) in \(S\), and let \(S_r\) be the disk enclosed by \(C_r\). Assume \(S_r\) is oriented with unit normal vector \({\bf e}\).

• (a) Let \(m(r)\) and \(M(r)\) be the minimum and maximum values of \({\bf curl}({\bf F}(P))\cdot{\bf e}\) for \(P\in S_r\). Prove that \[ m(r) \le \frac1{\pi r^2} \iint_{S_r\,} {\bf curl}({\bf F}) \cdot d{\bf S} \le M(r) \]
• (b) Prove that \[ {\bf curl}({\bf F}(Q))\cdot{\bf e} = \lim_{r\to 0} \frac1{\pi r^2}\int_{C_r} {\bf F}\cdot d{\bf s} \] This proves that \({\bf curl}({\bf F}(Q))\cdot{\bf e}\) is the circulation per unit area in the plane \(S\).