7.3 Trigonometric Substitution
Our next goal is to integrate functions involving one of the square root expressions: \[ \sqrt{a^2 - x^2},\qquad \sqrt{x^2+a^2},\qquad \sqrt{x^2 - a^2} \]
In each case, a substitution transforms the integral into a trigonometric integral.
EXAMPLE 1
Evaluate \(\displaystyle\int\sqrt{1-x^2}\,dx\).
Solution
Step 1. Substitute to eliminate the square root.
The integrand is defined for \(-1 \leq x \leq 1\), so we may set \(x = \sin\theta\), where \(-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}\).
414
Because \(\cos\theta\ge 0\) for such \(\theta\), we obtain the positive square root \[ \begin{eqnarray} \sqrt{1 - x^2} &=& \sqrt{ 1 - \sin^2\theta } = \sqrt{\cos^2\theta} = \cos\theta\tag{1} \end{eqnarray} \]
Step 2. Evaluate the trigonometric integral.
Since \(x = \sin\theta\), we have \(dx = \cos\theta\,d\theta\), and \(\sqrt{1 - x^2}\,dx = \cos\theta(\cos\theta\,d\theta)\). Thus \[ \int\sqrt{1-x^2}\,dx = \int \cos^2\theta\, d\theta = \frac12 \theta + \frac12 \sin \theta\cos\theta + C \]
Step 3. Convert back to the original variable.
It remains to express the answer in terms of \(x\): \[ x=\sin\theta,\qquad \theta = \sin^{-1}x, \qquad \sqrt{1-x^2}=\cos\theta\\ \]\[\int\sqrt{1-x^2}\,dx = \frac12 \theta + \frac12\sin \theta\cos\theta + C= \frac12\sin^{-1}x + \frac12x\sqrt{1-x^2} + C \]
Reminder
\[ \int \cos^2\theta\,d\theta = \frac12 \theta + \frac12 \sin \theta\cos\theta + C\]
Note: If \(x = a~\sin\theta\) and \(a > 0\), then \[ a^2 - x^2 = a^2(1 - \sin^2\theta) = a^2\cos^2\theta \] For \(-\frac{\pi}{2} \leq\theta \leq\frac{\pi}{2}\), \(\cos\theta \geq 0\) and thus \[ \sqrt{a^2 - x^2} = a~\cos\theta \]
Integrals Involving \(\sqrt{a^2 - x^2}\)
If \(\sqrt{a^2 - x^2}\) occurs in an integral where \(a > 0\), try the substitution \[ x = a~\sin\theta,\qquad dx = a~\cos\theta\, d\theta,\qquad \sqrt{a^2 - x^2} = a~\cos\theta \]
The next example shows that trigonometric substitution can be used with integrands involving \((a^2 - x^2)^{n/2}\), where \(n\) is any integer.
EXAMPLE 2 Integrand Involving \((a^2 - x^2)^{3/2}\)
Evaluate \(\int \frac{x^2}{(4 - x^2)^{3/2}}\, dx\).
Solution
Step 1. Substitute to eliminate the square root.
In this case, \(a = 2\) since \(\sqrt{4 - x^2} = \sqrt{2^2 - x^2}\). Therefore, we use \[ \begin{eqnarray*} &\displaystyle x = 2\sin\theta, \qquad dx = 2\cos\theta \,d\theta, \qquad \sqrt{4 - x^2} = 2\cos\theta \\ &\displaystyle \int \frac{x^2}{(4 - x^2)^{3/2}}\, dx = \int \frac{4\sin^2\theta}{2^3\cos^3\theta}\, 2\cos\theta\, d\theta = \int \frac{\sin^2\theta}{\cos^2\theta}\, d\theta = \int \tan^2\theta\, d\theta \end{eqnarray*} \]
Step 2. Evaluate the trigonometric integral.
Use the reduction formula in the marginal note with \(m=2\): \[ \int \tan^2\theta\, d\theta = \tan \theta-\int d\theta =\tan \theta -\theta + C \]
Reminder
\[ \int\tan^mx\,dx = \frac{\tan^{m-1}x}{m-1}-\int\tan^{m-2}x\,dx \]
We can also evaluate the integral using the identity \(\tan^2\theta=\sec^2\theta-1\).
Step 3. Convert back to the original variable.
We must write \(\tan \theta\) and \(\theta\) in terms of \(x\). By definition, \(x=2\sin\theta\), so \[ \sin\theta=\frac{x}2,\qquad \theta = \sin^{-1}\frac{x}2 \]

To express \(\tan\theta\) in terms of \(x\), we use the right triangle in Figure 7.1. The angle \(\theta\) satisfies \(\sin\theta=\dfrac{x}{2}\) and \[ \begin{align*} \tan\theta &= \frac{\text{opposite}}{\text{adjacent}}=\frac{x}{\sqrt{4-x^2}} \end{align*} \]
415
Thus we have \[ \begin{align*} \int \frac{x^2}{(4 - x^2)^{3/2}}\, dx &=\tan \theta -\theta + C= \frac{x}{\sqrt{4-x^2}}- \sin^{-1}\frac{x}2 +C \end{align*} \]
When the integrand involves \(\sqrt{x^2 + a^2}\), try the substitution \(x=a~\tan\theta\). Then \[ x^2+a^2=a^2~\tan^2\theta+a^2=a^2(1+\tan^2\theta)= a^2\sec^2\theta \]
and thus \(\sqrt{x^2 + a^2}=a~\sec\theta\).
In the substitution \(x = a~\tan\theta\), we choose \(-\frac{\pi}{2} <\theta < \frac{\pi}{2}\). Therefore, \(a~\sec\theta\) is the positive square root \(\sqrt{x^2 + a^2}\).
Integrals Involving \(\sqrt{x^2 + a^2}\)
If \(\sqrt{x^2 + a^2}\) occurs in an integral where \(a > 0\), try the substitution \[ x = a~\tan\theta,\qquad dx = a~\sec^2\theta\, d\theta,\qquad \sqrt{x^2 + a^2} = a~\sec \theta \]
EXAMPLE 3
Evaluate \(\displaystyle\int \sqrt{4x^2+20}\, dx\).
Solution First factor out a constant: \[ \int\sqrt{4x^2+20} \,dx= \int\sqrt{4(x^2+5)}\,dx = 2 \int\sqrt{x^2+5}\,dx \]
Thus we have the form \(\sqrt{x^2+a^2}\) with \(a = \sqrt 5\).
Step 1. Substitute to eliminate the square root.
\[ \begin{eqnarray*} &\displaystyle x = \sqrt 5~\tan\theta,\qquad dx = \sqrt 5\sec^2\theta\, d\theta, \qquad \sqrt{x^2+5} = \sqrt 5\sec\theta\\ &\displaystyle 2\int \sqrt{x^2+5}\, dx = 2\int \bigl(\sqrt 5\sec\theta\bigr)\, \sqrt 5\sec^2\theta\, d\theta = 10\int \sec^3\theta\, d\theta \end{eqnarray*} \]
Step 2. Evaluate the trigonometric integral.
Apply the reduction formula recalled in the margin with \(m=3\): \[ \begin{align} \int\sqrt{4x^2+20} \,dx=10\int \sec^3\theta\, d\theta&= 10\frac{\tan\theta\sec \theta}2 + 10\left(\frac12\right)\int\sec\theta\, dx \notag\\ &= 5~\tan\theta\sec \theta + 5\ln ({\sec \theta + \tan \theta} ) +C \notag \end{align} \]
Reminder
\[ \begin{eqnarray*} \int \sec^m x\, dx &=& \frac{\tan x~\sec^{m-2} x}{m-1}\\ &&{}+ \frac{m-2}{m-1}\int \sec^{m-2} x\, dx \end{eqnarray*} \]
Note: It is not necessary to write \(\ln |\sec\theta +\tan\theta|\) with the absolute value because our substitution \(x=\sqrt{5} \tan \theta\) assumes that \(-\frac{\pi}{2} < \theta < \frac{\pi}{2}\), where \(\sec \theta + \tan \theta >0\).
Step 3. Convert back to the original variable.
Since \(x = \sqrt5\tan\theta\), we use the right triangle in Figure 7.2.
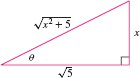
\[ \begin{align*} \tan\theta &= \frac{\text{opposite}}{\text{adjacent}} = \frac{x}{\sqrt5},\qquad \sec \theta = \frac{\text{hypotenuse}}{\text{adjacent}} = \frac{\sqrt{x^2+5}}{\sqrt5}\\ \int \sqrt{4x^2+20}\, dx &= 5\,\frac{x}{\sqrt 5}\frac{\sqrt{x^2+5}}{\sqrt 5} + 5\ln\left(\frac{\sqrt{x^2+5}}{\sqrt 5} + \frac{x}{\sqrt 5}\right)+C \\ &= x\sqrt{x^2+5} + 5\ln\left(\frac{\sqrt{x^2+5}+x}{\sqrt 5} \right) +C \end{align*} \]
416
The logarithmic term can be rewritten as \[ \begin{align*} 5\ln\left(\frac{\sqrt{x^2+5}+x}{\sqrt 5} \right)+C &= 5\ln\Big( \sqrt{x^2+5} + x \Big) -\underbrace{5\ln\sqrt{5} +C}_{\textrm{Constant}} \end{align*} \]
Since the constant \(C\) is arbitrary, we can absorb \(-5\ln{\sqrt 5}\) into \(C\) and write \[ \int \sqrt{4x^2+20}\, dx = x\sqrt{x^2+5} + 5\ln\Big( \sqrt{x^2+5} + x \Big)+C \]
Our last trigonometric substitution \(x=a~\sec\theta\) transforms \(\sqrt{x^2-a^2}\) into \(a~\tan\theta\) because \[ x^2-a^2=a^2\sec^2\theta-a^2=a^2(\sec^2\theta - 1)=a^2~\tan^2\theta \]
In the substitution \(x = a~\sec\theta\), we choose \(0 \leq\theta < \frac{\pi}{2}\) if \(x \geq a\) and \(\pi \leq \theta < \frac{3\pi}{2}\) if \(x \leq -a\). With these choices, \(a~\tan\theta\) is the positive square root \(\sqrt{x^2 - a^2}\).
Integrals Involving \(\sqrt{x^2-a^2}\)
If \(\sqrt{x^2 - a^2}\) occurs in an integral where \(a > 0\), try the substitution \[ x = a~\sec\theta,\qquad dx = a~\sec\theta \tan\theta\, d\theta,\qquad \sqrt{x^2 - a^2} = a~\tan\theta \]
EXAMPLE 4
Evaluate \(\displaystyle\int \dfrac{dx}{x^2\sqrt{x^2 - 9}} \).
Solution In this case, make the substitution \[ x = 3\sec \theta, \qquad dx = 3\sec \theta \tan \theta\, d\theta,\qquad \sqrt{x^2 - 9} = 3\tan\theta \] \[ \int \dfrac{dx}{x^2\sqrt{x^2 - 9}} = \int \dfrac{3\sec \theta \tan \theta\, d\theta}{(9\sec^2\theta)(3\tan\theta)} = \frac{1}{9} \int \cos\theta\, d\theta = \frac{1}{9} \sin\theta +C \]
Since \(x = 3\sec \theta\), we use the right triangle in Figure 7.3: \[ \sec\theta = \frac{\textrm{hypotenuse}}{\textrm{adjacent}} = \frac{x}3,\qquad \sin\theta = \frac{\textrm{opposite}}{\textrm{hypotenuse}} = \frac{\sqrt{x^2 - 9}}{x} \]
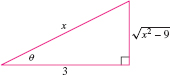
Therefore, \[ \int \frac{dx}{x^2\sqrt{x^2 - 9}} = \frac{1}9 \sin\theta +C =\frac{\sqrt{x^2 -9}}{9x}+ C \]
So far we have dealt with the expressions \(\sqrt{x^2 \pm a^2}\) and \(\sqrt{a^2 - x^2}\). By completing the square (Section 1.2), we can treat the more general form \(\sqrt{ax^2 + bx + c}\).
EXAMPLE 5 Completing the Square
Evaluate \(\displaystyle\int \dfrac{dx}{(x^2 - 6x + 11)^2}\).
Solution
Step 1. Complete the square. \[ x^2 - 6x + 11 = (x^2-6x+9)+2= \underbrace{(x - 3)^2}_{u^2} + 2 \]
417
Step 2. Use substitution.
Let \(u = x-3\), \(du = dx\): \[ \int \dfrac{dx}{(x^2 - 6x + 11)^2} = \int \dfrac{du}{(u^2 + 2)^2}\tag{2} \]
Step 3. Trigonometric substitution.
Evaluate the \(u\)-integral using trigonometric substitution: \[ u = \sqrt 2 \tan \theta, \qquad \sqrt{u^2 + 2} = \sqrt 2\sec\theta, \qquad du = \sqrt 2 \sec^2 \theta \, d\theta \] \[ \begin{align} \int \frac{du}{(u^2 + 2)^2} &= \int \frac{\sqrt 2 \sec^2 \theta\,d\theta}{4\sec^4\theta} = \frac1{2\sqrt2}\int \cos^2\theta\, d\theta \notag\\ &=\frac1{2\sqrt 2}\left(\frac{\theta}2+\frac{\sin\theta\cos\theta}2\right)+C\tag{3} \end{align} \]
Reminder
\[ \int\cos^2\theta\,d\theta=\frac{\theta}2+\frac{\sin\theta\cos\theta}2 + C \]
Since \(\theta =\tan^{-1} \dfrac{u}{\sqrt 2}\), we use the right triangle in Figure 7.4 to obtain \[ \sin\theta\cos\theta = \left(\frac{\textrm{opposite}}{\textrm{hypotenuse}}\right)\left(\frac{\textrm{adjacent}}{\textrm{hypotenuse}} \right) =\frac{u}{\sqrt{u^2+2}}\cdot\frac{\sqrt 2}{\sqrt{u^2+2}} = \frac{\sqrt2 u}{u^2 + 2} \]
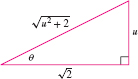
Thus, Eq. (3) becomes \[ \begin{eqnarray} \int \frac{du}{(u^2 + 2)^2} &=& \frac1{4\sqrt2} \left(\tan^{-1} \frac{u}{\sqrt 2} + \frac{\sqrt 2\,u}{u^2 + 2}\right) + C\nonumber\\ &=& \frac{1}{4\sqrt 2} \tan^{-1} \frac{u}{\sqrt 2} + \frac{u}{4(u^2+2)}+C\tag{4} \end{eqnarray} \]
Step 4. Convert to the original variable.
Since \(u = x-3\) and \(u^2+2=x^2 - 6x + 11\), Eq. (4) becomes \[ \int \frac{du}{(u^2 + 2)^2} = \frac1{4\sqrt2}\tan^{-1} \frac{x-3}{\sqrt 2} +\frac{x-3}{4(x^2 - 6x + 11)} + C \]
This is our final answer by Eq. (2): \[ \int \dfrac{dx}{(x^2 - 6x + 11)^2} = \frac1{4\sqrt2}\tan^{-1} \frac{x-3}{\sqrt 2} +\frac{x-3}{4(x^2 - 6x + 11)} + C \]
7.3.1 Summary
- Trigonometric substitution:
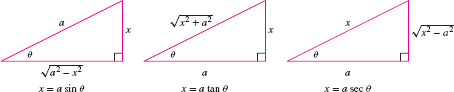
Square root form in integrand Trigonometric substitution \(\sqrt{a^2-x^2}\) \(x = a~\sin\theta\),\(\quad\) \(dx =a~\cos\theta\,d\theta\),\(\quad\) \(\sqrt{a^2-x^2}=a~\cos\theta\) \(\sqrt{x^2+a^2}\) \(x = a~\tan\theta\),\(\quad\) \(dx = a~\sec^2\theta\,d\theta\),\(\quad\) \(\sqrt{x^2+a^2}=a~\sec\theta\) \(\sqrt{x^2-a^2}\) \(x = a~\sec\theta\),\(\quad\) \(dx = a~\sec\theta\tan\theta\,d\theta\),\(\quad\) \(\sqrt{x^2-a^2}=a~\tan\theta\) Step 1. Substitute to eliminate the square root.
Step 2. Evaluate the trigonometric integral.
Step 3. Convert back to the original variable.
418
- The three trigonometric substitutions correspond to three right triangles (Figure 7.5) that we use to express the trigonometric functions of \(\theta\) in terms of \(x\).
- Integrands involving \(\sqrt{x^2+bx+c}\) are treated by completing the square (see Example 5).