7.5 The Method of Partial Fractions

The Method of Partial Fractions is used to integrate rational functions \[ f(x) = \dfrac{P(x)}{Q(x)} \]

where \(P(x)\) and \(Q(x)\) are polynomials. The idea is to write \(f(x)\) as a sum of simpler rational functions that can be integrated directly. For example, in the simplest case we use the identity \[ \frac1{x^2-1} = \frac{\frac{1}{2}}{x-1} - \frac{\frac{1}{2}}{x+1} \]

to evaluate the integral \[ \int\frac{dx}{x^2-1} = \frac12\int\frac{dx}{x-1} - \frac12\int\frac{dx}{x+1}=\frac12\ln|x-1|-\frac12\ln|x+1| \]

It is a fact from algebra (known as the “Fundamental Theorem of Algebra”) that every polynomial \(Q(x)\) with real coefficients can be written as a product of linear and quadratic factors with real coefficients. However, it is not always possible to find these factors explicitly.

A rational function \({P(x)}/{Q(x)}\) is called proper if the degree of \(P(x)\) [denoted \(\deg(P)\)] is less than the degree of \(Q(x)\). For example, \[ \underbrace{\frac{x^2 -3x+7}{x^4-16}}_{\textrm{Proper}},\qquad \underbrace{\frac{2x^2 + 7}{x-5},\qquad \frac{x-2}{x-5}}_{\textrm{Not proper}} \]

427

Suppose first that \({P(x)}/{Q(x)}\) is proper and that the denominator \(Q(x)\) factors as a product of distinct linear factors. In other words, \[ \frac{P(x)}{Q(x)} = \frac{P(x)}{(x-a_1)(x-a_2)\cdots (x-a_n)} \]

Each distinct linear factor \((x-a)\) in the denominator contributes a term \[ \frac{A}{x-a} \] to the partial fraction decomposition.

where the roots \(a_1, a_2, \dots , a_n\) are all distinct and \(\deg(P) < n\). Then there is a partial fraction decomposition: \[ \frac{P(x)}{Q(x)} = \frac{A_1}{(x-a_1)}+\frac{A_2}{(x-a_2)}+\cdots+ \frac{A_n}{(x-a_n)} \]

for suitable constants \(A_1, \dots, A_n\). For example, \[ \frac{5x^2+x-28}{(x+1)(x-2)(x-3)} = -\frac2{x + 1} + \frac2{x - 2} + \frac5{x - 3} \]

Once we have found the partial fraction decomposition, we can integrate the individual terms.

EXAMPLE 1 Finding the Constants

Evaluate \(\int \frac{dx}{x^2-7x+10}\).

Solution The denominator factors as \(x^2-7x+10=(x-2)(x-5)\), so we look for a partial fraction decomposition: \[ \frac1{(x-2)(x-5)} = \frac{A}{x-2} + \frac{B}{x-5} \]

To find \(A\) and \(B\), first multiply by \((x-2)(x-5)\) to clear denominators: \[ \begin{align} 1& = (x-2)(x-5)\left(\frac{A}{x-2} + \frac{B}{x-5}\right)\notag\\ 1&=A(x-5) + B(x-2)\tag{1} \end{align} \]

This equation holds for all values of \(x\) (including \(x = 2\) and \(x = 5\), by continuity). We determine \(A\) by setting \(x = 2\) (this makes the second term disappear): \[ 1 = A(2-5) + \underbrace{B(2 - 2)}_{\textrm{This is zero}} = -3A\quad\Rightarrow\quad \boxed{\bbox[#FAF8ED,5pt]{A=-\frac{1}{3}}} \]

Similarly, to calculate \(B\), set \(x = 5\) in Eq. (1): \[ 1 = A(5-5) + B(5-2) = 3B \quad \Rightarrow\quad\boxed{\bbox[#FAF8ED,5pt]{B= \frac{1}{3}}} \]

The resulting partial fraction decomposition is \[ \boxed{\bbox[#FAF8ED,5pt]{\frac{1}{(x-2)(x-5)} = \frac{-\frac13}{x-2} + \frac{\frac13}{x- 5}}} \]

428

The integration can now be carried out: \[ \begin{eqnarray*} \int \frac{dx}{(x-2)(x-5)} &=& -\frac{1}{3}\int \frac{dx}{x-2} + \frac{1}{3}\int\frac{dx}{x-5} \\ &=& -\frac{1}{3}\ln|x-2| + \frac{1}{3}\ln|x-5| + C \end{eqnarray*} \]

In Eq. (2), the linear factor \(2x-8\) does not have the form \((x-a)\) used previously, but the partial fraction decomposition can be carried out in the same way.

EXAMPLE 2

Evaluate \(\int \frac{x^2 +2}{(x-1)(2x-8)(x+2)}\, dx\).

Solution

Step 1. Find the partial fraction decomposition.

The decomposition has the form \[ \frac{x^2 +2}{(x-1)(2x-8)(x+2)} = \frac{A}{x-1} + \frac{B}{2x-8} + \frac{C}{x+2}\tag{2} \]

As before, multiply by \((x-1)(2x-8)(x+2)\) to clear denominators: \[ x^2 +2 = A(2x-8)(x+2) + B(x-1)(x+2) + C(x-1)(2x-8)\tag{3} \]

Since \(A\) goes with the factor \((x-1)\), we set \(x = 1\) in Eq.(3) to compute \(A\): \[ \begin{align*} 1^2+2 &= A(2-8)(1+2) + \overbrace{B(1-1)(1+2) + C(1-1)(2-8)}^{\textrm{Zero}}\\ 3 &= -18A\quad\Rightarrow\quad \boxed{\bbox[#FAF8ED,5pt]{A= -\frac{1}{6}}} \end{align*} \]

Similarly, 4 is the root of \(2x-8\), so we compute \(B\) by setting \(x = 4\) in Eq.(3): \[ \begin{align*} 4^2+2 &= A(8-8)(4+2) + B(4 - 1)(4 + 2)+C(4-1)(8-8)\\ 18 &= 18B\quad\Rightarrow\quad \boxed{\bbox[#FAF8ED,5pt]{B= 1}} \end{align*} \]

Finally, \(C\) is determined by setting \(x= -2\) in Eq. (3): \[ \begin{align*} (-2)^2+2 & = A(-4-8)(-2+2) + B(-2 - 1)(-2 + 2)+C(-2-1)(-4-8)\\ 6 &= 36C\quad\Rightarrow\quad \boxed{\bbox[#FAF8ED,5pt]{C= \frac{1}{6}}} \end{align*} \]

The result is \[ \boxed{\bbox[#FAF8ED,5pt]{\frac{x^2 +2}{(x-1)(2x-8)(x+2)} = -\frac{\frac16}{x-1} + \frac{1}{2x-8} + \frac{\frac16}{x+2}}} \]

Step 2. Carry out the integration. \[ \begin{eqnarray*} \int \frac{x^2 + 2}{(x-1)(2x-8)(x+2)}\, dx &=& -\frac16\int \frac{dx}{x-1} + \int \frac{dx}{2x-8} + \frac16\int \frac{dx}{x+2}\\ &=& -\frac16\ln\big|x-1\big| + \frac12\ln\big|2x-8\big| + \frac16\ln\big|x+2\big|+ C \end{eqnarray*} \]

429

If \({P(x)}/{Q(x)}\) is not proper—that is, if \(\deg(P) \geq \deg(Q)\)—we use long division to write \[ \frac{P(x)}{Q(x)} = g(x) + \frac{R(x)}{Q(x)} \]

where \(g(x)\) is a polynomial and \({R(x)}/{Q(x)}\) is proper. We may then integrate \( {P(x)}/{Q(x)}\) using the partial fraction decomposition of \({R(x)}/{Q(x)}\).

Long division:
image

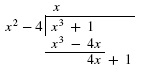
The quotient \(\dfrac{x^3 + 1}{x^2 - 4}\) is equal to \(x\) with remainder \(4x + 1\).

EXAMPLE 3 Long Division Necessary

Evaluate \(\displaystyle\int \dfrac{x^3 + 1}{x^2 - 4}\, dx\).

Solution Using long division, we write \[ \dfrac{x^3 + 1}{x^2 - 4} = x + \frac{4x + 1}{x^2 - 4} = x + \frac{4x + 1}{(x - 2)(x + 2)} \]

It is not hard to show that the second term has a partial fraction decomposition: \[ \frac{4x + 1}{(x-2)(x+2)} = \frac{\frac94}{x - 2} + \frac{\frac74}{x+2} \]

Therefore, \[ \begin{eqnarray*} \int \dfrac{(x^3 + 1)\, dx}{x^2 - 4} &=& \int x\, dx + \frac94 \int \frac{dx}{x-2} + \frac74 \int \frac{dx}{x+2}\\ &=& \frac12x^2 + \frac94\ln\big|x-2\big| + \frac74\ln\big|x+2\big| +C \end{eqnarray*} \]

Now suppose that the denominator has repeated linear factors: \[ \frac{P(x)}{Q(x)} = \frac{P(x)} {(x - a_1)^{M_1}(x-a_2)^{M_2}\cdots (x - a_n)^{M_n}} \]

Each factor \((x-a_i)^{M_i}\) contributes the following sum of terms to the partial fraction decomposition: \[ \frac{B_1}{(x-a_i)} + \frac{B_2}{(x-a_i)^2} + \cdots + \frac{B_{M_i}}{(x-a_i)^{M_i}} \]

EXAMPLE 4 Repeated Linear Factors

Evaluate \(\displaystyle\int \dfrac{3x - 9}{(x-1)(x+2)^2} \, dx\).

Solution We are looking for a partial fraction decomposition of the form \[ \frac{3x - 9}{(x-1)(x+2)^2} = \frac{A}{x-1} +\frac{B_1}{x+2}+\frac{B_2}{(x+2)^2} \]

Let's clear denominators to obtain \[ 3x - 9 = A(x+2)^2 + B_1(x-1)(x+2) + B_2(x-1)\tag{4} \]

We compute \(A\) and \(B_2\) by substituting in Eq. (4) in the usual way:

  • Set \(x = 1\): This gives \(-6 = 9A\), or \(\boxed{\bbox[#FAF8ED,5pt]{A = -\frac{2}{3}}}\).
  • Set \(x = -2\): This gives \(-15 = -3B_2\), or \(\boxed{\bbox[#FAF8ED,5pt]{B_2 = 5}}\).

    430

With these constants, Eq. (4) becomes \[ 3x - 9 = -\frac{2}{3}(x+2)^2 + B_1(x-1)(x+2) + 5(x-1)\tag{5} \]

We cannot determine \(B_1\) in the same way as \(A\) and \(B_2\). Here are two ways to proceed.

  • First method (substitution): There is no use substituting \(x=1\) or \(x=-2\) in Eq. (5) because the term involving \(B_1\) drops out. But we are free to plug in any other value of \(x\). Let's try \(x=2\) in Eq.(5): \[ \begin{align*} 3(2) - 9 &= -\frac{2}{3}(2+2)^2 + B_1(2-1)(2+2) + 5(2-1)\\ -3 &= -\frac{32}{3} + 4B_1 + 5 \\ B_1 &= \frac14\left(-8 + \frac{32}{3}\right) = \frac23 \end{align*} \]
  • Second method (undetermined coefficients): Expand the terms in Eq. (5): \[ \begin{align*} 3x-9 &= -\frac{2}{3}(x^2 + 4x + 4) + B_1(x^2 + x - 2) + 5(x-1) \end{align*} \]

    The coefficients of the powers of \(x\) on each side of the equation must be equal. Since \(x^2\) does not occur on the left-hand side, \(0 = -\frac23 +B_1\), or \(B_1 = \frac23\).

Either way, we have shown that \[ \boxed{\bbox[#FAF8ED,5pt]{\frac{3x - 9}{(x-1)(x+2)^2} = -\frac{\frac23}{x-1} + \frac{\frac23}{x+2} + \frac{5}{(x+2)^2}}} \] \[ \begin{eqnarray*} \int \frac{3x - 9}{(x-1)(x+2)^2}\, dx &=& -\frac{2}{3}\int\frac{dx}{x- 1} + \frac{2}{3}\int \frac{dx}{x+2} + 5\int \frac{dx}{(x+2)^2}\\ &=& -\frac{2}{3}\ln\big|x-1\big| + \frac{2}{3}\ln\big|x+2\big| - \frac{5}{x+2} + C \end{eqnarray*} \]

Quadratic Factors

A quadratic polynomial \(ax^2 + bx + c\) is called irreducible if it cannot be written as a product of two linear factors (without using complex numbers). A power of an irreducible quadratic factor \((ax^2 + bx + c)^M\) contributes a sum of the following type to a partial fraction decomposition: \[ \frac{A_1x+B_1}{ax^2+bx+c} + \frac{A_2x+B_2}{(ax^2+bx+c)^2} +\cdots + \frac{A_Mx+B_M}{(ax^2+bx+c)^M} \]

For example, \[ \frac{4-12x}{(x+1)(x^2+x+4)^2} = \frac1{x+1} -\frac{x}{x^2 +x+4} - \frac{4x+12}{(x^2 +x+4)^2} \]

You may need to use trigonometric substitution to integrate these terms. In particular, the following result may be useful (see Exercise 33 in Section 7.3). \[ \boxed{\bbox[#FAF8ED,5pt]{\int \frac{dx}{x^2 + a} = \frac{1}{\sqrt a} \tan^{-1}\left(\frac{x}{\sqrt a}\right) + C \quad \textrm{(for \(a>0\))}}}\tag{6} \]

Reminder

If \(b>0\), then \(x^2+b\) is irreducible, but \(x^2-b\) is reducible because \[ x^2-b = \bigl(x+\sqrt{b}\bigr)\bigl(x-\sqrt{b}\bigr) \]

431

EXAMPLE 5 Irreducible versus Reducible Quadratic Factors

Evaluate

  1. \(\displaystyle\int \frac{18}{(x+3)(x^2+9)}\, dx\)
  2. \(\displaystyle\int \frac{18}{(x+3)(x^2-9)}\, dx\)

Solution

(a) The quadratic factor \(x^2+9\) is irreducible, so the partial fraction decomposition has the form \[ \boxed{\bbox[#FAF8ED,5pt] {\frac{18}{(x+3)(x^2+9)} = \frac{A}{x+3} + \frac{Bx +C}{x^2 + 9} }} \]

Clear denominators to obtain \[ 18 = A(x^2+9) + (Bx +C)(x+3)\tag{7} \]

To find \(A\), set \(x=-3\): \[ 18= A\big((-3)^2+9\big) + 0\quad\Rightarrow\quad \boxed{\bbox[#FAF8ED,5pt]{A=1}} \]

Then substitute \(A = 1\) in Eq. (7) to obtain \[ 18 = (x^2+9) + (Bx +C)(x+3) = (B+1)x^2+(C+3B)x+(9+3C) \]

Equating coefficients, we get \(B+1=0\) and \(9+3C=18\). Hence (see margin): \[ \boxed{\bbox[#FAF8ED,5pt]{B=-1,\qquad C=3}} \] \[ \begin{align*} \int\frac{18\,dx}{(x+3)(x^2+9)} &= \int\frac{dx}{x+3} + \int\frac{(-x + 3)\,dx}{x^2 + 9} \\ &= \int\frac{dx}{x+3} - \int\frac{x\,dx }{x^2 + 9} + \int\frac{3\, dx}{x^2 + 9}\\ &= \ln\big|x+3\big| - \frac{1}{2}\ln(x^2+9) + \tan^{-1} \frac{x}{3} + C \end{align*} \]

In the second equality, we use \[ \begin{align*} \int \frac{x\,dx}{x^2 + 9} &= \frac{1}{2} \int \frac{du}{u} = \frac{1}{2}\ln(x^2+9) +C \end{align*} \]

and Eq. (6): \[ \begin{align*} \int \dfrac{dx}{x^2 + 9} &= \frac13\tan^{-1} \dfrac{x}{3} + C \end{align*} \]

(b) The polynomial \(x^2-9\) is not irreducible because \(x^2-9 = (x-3)(x+3)\). Therefore, the partial fraction decomposition has the form \[\boxed{\bbox[#FAF8ED,5pt]{ \frac{18}{(x+3)(x^2-9)} = \frac{18}{(x+3)^2(x-3) } = \frac{A}{x-3} + \frac{B}{x+3} + \frac{C}{(x+3)^2}} }\]

Clear denominators: \[ 18 = A(x+3)^2 + B(x+3)(x-3) + C(x-3) \]

For \(x=3\), this yields \(18=(6^2)A\), and for \(x=-3\), this yields \(18=-6C\). Therefore, \[ \boxed{\bbox[#FAF8ED,5pt]{A=\frac12, \quad C=-3}}\quad \Rightarrow\quad 18 = \frac12(x+3)^2 + B(x+3)(x-3) -3(x-3) \]

432

To solve for \(B\), we can plug in any value of \(x\) other than \(\pm 3\). The choice \(x=2\) yields \(18 = \frac12(25)- 5B +3\), or \(B= -\frac12\), and \[ \begin{align*} \int \frac{18}{(x+3)(x^2-9)}\, dx &= \frac12\int \frac{dx}{x-3} -\frac12\int \frac{dx}{x+3} -3\int \frac{dx}{(x+3)^2} \\ &= \frac12\ln\big|x-3\big| - \frac12\ln\big|x+3\big| +3(x+3)^{-1} +C \end{align*} \]

EXAMPLE 6 Repeated Quadratic Factor

Evaluate \(\int \frac{4-x}{x(x^2+2)^2}\, dx\).

Solution The partial fraction decomposition has the form \[ \frac{4-x}{x(x^2+2)^2} = \frac{A}{x}+\frac{Bx+C}{x^2+2}+ \frac{Dx+E}{(x^2+2)^2} \]

Clear denominators by multiplying through by \(x(x^2 + 2)^2\): \[ 4-x = A(x^2+2)^2 + (Bx+C)\big(x(x^2+2)\big) + (Dx+E)x\tag{8} \]

We compute \(A\) directly by setting \(x=0\). Then Eq. (8) reduces to \(4=4A\), or \(A=1\). We find the remaining coefficients by the method of undetermined coefficients. Set \(A=1\) in Eq. (8) and expand: \[ \begin{align*} 4-x &= (x^4+4x^2+4)+(Bx^4+2Bx^2+Cx^3+2C) + (Dx^2+Ex)\\ &= (1+B)x^4+Cx^3+(4+2B+D)x^2+Ex + 2C +4 \end{align*} \]

Now equate the coefficients on the two sides of the equation: \[ \begin{alignat*}{2} 1+B&=0&\qquad &\textrm{(Coefficient of \(x^4\))}\\ C&=0&\qquad &\textrm{(Coefficient of \(x^3\))}\\ 4+2B+D&=0&\qquad &\textrm{(Coefficient of \(x^2\))}\\ E&=-1&\qquad &\textrm{(Coefficient of \(x\))}\\ 2C + 4 &= 4&\qquad&\textrm{(Constant term)} \end{alignat*} \]

These equations yield \(B=-1\), \(C=0\), \(D=-2\), and \(E=-1\). Thus, \[ \begin{align*} \int\frac{(4-x)\,dx}{x(x^2+2)^2} &= \int \frac{dx}{x}-\int \frac{x\,dx}{x^2+2} - \int \frac{(2x+1)\,dx}{(x^2+2)^2}\\ &= \ln|x|-\frac12\ln(x^2+2) - \int \frac{(2x+1)dx}{(x^2+2)^2} \end{align*} \]

The middle integral was evaluated using the substitution \(u=x^2+2\), \(du = 2x\,dx\). The third integral breaks up as a sum: \[ \begin{align} \int\frac{(2x+1)\,dx}{(x^2+2)^2} &= \overbrace{\int\frac{2x\,dx}{(x^2+2)^2}}^{\textrm{Use substitution \(u=x^2+2\)}} + \int\frac{dx}{(x^2+2)^2}\notag\\ & = - (x^2+2)^{-1} + \int\frac{dx}{(x^2+2)^2} \tag{9} \end{align} \]

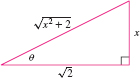
To evaluate the integral in Eq. (9), we use the trigonometric substitution \[ x = \sqrt 2\tan \theta,\qquad dx=\sqrt 2\sec^2\theta\,d\theta,\qquad x^2+2 = 2\tan^2\theta+2 = 2\sec^2\theta \]

433

Referring to Figure 7.7, we obtain \[ \begin{align*} \int\frac{dx}{(x^2+2)^2} &= \int\frac{\sqrt 2\sec^2\theta\,d\theta}{(2\tan^2 \theta+2)^2} = \int\frac{\sqrt 2\sec^2\theta\,d\theta}{4\sec^4\theta} \\ &= \frac{\sqrt 2}4\int \cos^2\theta\,d\theta = \frac{\sqrt 2}4 \left(\frac12 \theta +\frac12\sin \theta\cos \theta \right)+C\\ &= \frac{\sqrt 2}8 \tan^{-1}\frac{x}{\sqrt 2} +\frac{\sqrt 2}8 \frac{x}{\sqrt{x^2+2}} \frac{\sqrt 2}{\sqrt{x^2+2}} + C\\ &= \frac1{4\sqrt 2} \tan^{-1}\frac{x}{\sqrt 2} +\frac{1}4\frac{x}{x^2+2} +C \end{align*} \]

image

Collecting all the terms, we have \[ \begin{eqnarray*} \int \frac{4-x}{x(x^2+2)^2}\, dx &=& \ln |x| -\frac12\ln(x^2+2) + \frac{1-\frac14 x}{x^2+2} - \frac1{4\sqrt 2} \tan^{-1}\frac{x}{\sqrt 2} +C \end{eqnarray*} \]

CONCEPTUAL INSIGHT

The examples in this section illustrate a general fact: The integral of a rational function can be expressed as a sum of rational functions, arctangents of linear or quadratic polynomials, and logarithms of linear or quadratic polynomials (provided that we can factor the denominator). Other types of functions, such as exponential and trigonometric functions, do not appear.

Using a Computer Algebra System

Finding partial fraction decompositions often requires laborious computation. Fortunately, most computer algebra systems have a command that produces partial fraction decompositions (with names such as “Apart” or “parfrac”). For example, the command \[ \mathtt{Apart[(x}\textrm{^} \mathtt{2 - 2)/((x + 2)(x} \textrm{^} \mathtt{2 + 4)} \textrm{^} \mathtt{3)]} \]

produces the partial fraction decomposition \[ \frac{x^2 - 2}{(x + 2)(x^2 + 4)^3} = \frac1{256 (2 + x)} + \frac{3(x-2)}{4(4 + x^2)^3} + \frac{2-x}{32(4 + x^2)^2} +\frac{2-x}{256(4 + x^2)} \]

However, a computer algebra system cannot produce a partial fraction decomposition in cases where \(Q(x)\) cannot be factored explicitly.

The polynomial \(x^5+2x+2\) cannot be factored explicitly, so the command \[ \mathtt{Apart[1/(x}\textrm{^}\mathtt{5+2x+2)]} \]

returns the useless response \[ \frac1{x^5+2x+2} \]

7.5.1 Summary

Method of Partial Fractions: Assume first that \(P(x)/Q(x)\) is a proper rational function [that is, \(\deg(P) < \deg(Q)\)] and that \(Q(x)\) can be factored explicitly as a product of linear and irreducible quadratic terms.