8.2 Fluid Pressure and Force
Fluid force is the force on an object submerged in a fluid. Divers feel this force as they descend below the water surface (Figure 8.11). Our calculation of fluid force is based on two laws that determine the pressure exerted by a fluid:
- Fluid pressure \(p\) is proportional to depth.
- Fluid pressure does not act in a specific direction. Rather, a fluid exerts pressure on each side of an object in the perpendicular direction (Figure 8.12).
This second fact, known as Pascal's principle, points to an important difference between fluid pressure and the pressure exerted by one solid object on another.

Pressure, by definition, is force per unit area.
- The SI unit of pressure is the pascal (Pa) \((1 Pa = 1 N/m^2)\).
- Mass density (mass per unit volume) is denoted \(\rho\) (Greek rho).
- The factor \(\rho g\) is the density by weight, where \(g=9.8 m/s^2\) is the acceleration due to gravity.
Fluid Pressure
The pressure \(p\) at depth \(h\) in a fluid of mass density \(\rho\) is \[ \boxed{\bbox[#FAF8ED,5pt]{p = \rho gh}}\tag{1} \]
The pressure acts at each point on an object in the direction perpendicular to the object's surface at that point.
Our first example does not require integration because the pressure \(p\) is constant. In this case, the total force acting on a surface of area \(A\) is \[ \boxed{\bbox[#FAF8ED,5pt]{\mathrm{Force = pressure \times area} = pA}} \]
EXAMPLE 1
Calculate the fluid force on the top and bottom of a box of dimensions \(2\times 2\times 5\) m, submerged in a pool of water with its top 3 m below the water surface (Figure 8.12). The density of water is \(\rho = 10^3\) kg/m\(^3\).
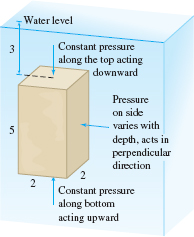
Solution The top of the box is located at depth \(h=3\) m, so, by Eq. (1) with \(g=9.8\), \[\textrm{Pressure on top} = \rho g h = 10^3(9.8)(3) = 29{,}400 \mathrm{Pa} \]
The top has area \(A=4 \mathrm{m}^2\) and the pressure is constant, so \[ \textrm{Downward force on top} = pA = 10^3(9.8)(3)\times 4 = 117{,}600 \textrm{N} \]
The bottom of the box is at depth \(h=8\) m, so the total force on the bottom is \[ \textrm{Upward force on bottom} = pA = 10^3(9.8)(8) \times 4 = 313{,}600 \mathrm{N} \]
In the next example, the pressure varies with depth, and it is necessary to calculate the force as an integral.
EXAMPLE 2 Calculating Force Using Integration
Calculate the fluid force \(F\) on the side of the box in Example 1.
Solution Since the pressure varies with depth, we divide the side of the box into \(N\) thin horizontal strips (Figure 8.13). Let \(F_j\) be the force on the \(j\)th strip. The total force \(F\) is equal to the sum of the forces on the strips: \[ F = F_1 + F_2 + \cdots + F_N \]
475
Step 1. Approximate the force on a strip.
We'll use the variable \(y\) to denote depth, where \(y=0\) at the water level and \(y\) is positive in the downward direction. Thus, a larger value of \(y\) denotes greater depth. Each strip is a rectangle of height \(\Delta y = 5/N\) and length 2, so the area of a strip is \(2\Delta y\). The bottom edge of the \(j\)th strip has depth \(y_j=3+j\Delta y\).
If \(\Delta y\) is small, the pressure on the \(j\)th strip is nearly constant with value \(\rho gy_j\) (because all points on the strip lie at nearly the same depth \(y_j\)), so we can approximate the force on the \(j\)th strip: \[ F_j \approx \underbrace{\rho g y_j}_{\mathrm{Pressure}}\times \underbrace{(2\Delta y)}_{\mathrm{Area}} = (\rho g) 2 y_j \Delta y \]

Step 2. Approximate total force as a Riemann sum. \[ F = F_1 + F_2 + \cdots + F_N \approx \rho g\sum_{j = 1}^N 2 y_j \Delta y \]
The sum on the right is a Riemann sum that converges to the integral \({\rho g \int_3^8 2y\, dy}\). The interval of integration is \([3,8]\) because the box extends from \(y=3\) to \(y=8\) (the Riemann sum has been set up with \(y_0=3\) and \(y_N =8\)).
Step 3. Evaluate total force as an integral.
As \(\Delta y\) tends to zero, the Riemann sum approaches the integral, and we obtain \[ F = \rho g\int_3^8 2y\, dy = (\rho g)y^2 \bigg|_3^8= (10^3)(9.8) (8^2- 3^2) = {539{,}000} \textrm{N} \]
Now we'll add another complication: allowing the widths of the horizontal strips to vary with depth (Figure 8.14). Denote the width at depth \(y\) by \(f(y)\): \[ f(y) = \hbox{width of the side at depth \(y\)} \]
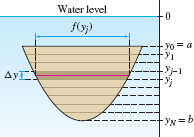
As before, assume that the object extends from \(y=a\) to \(y=b\). Divide the flat side of the object into \(N\) horizontal strips of thickness \(\Delta y=(b-a)/N\). If \(\Delta y\) is small, the \(j\)th strip is nearly rectangular of area \(f(y)\Delta y\). Since the strip lies at depth \(y_j=a+j\Delta y\), the force \(F_j\) on the \(j\)th strip can be approximated: \[ F_j \approx \underbrace{\rho g y_j}_{\mathrm{Pressure}}\times \underbrace{f(y_j)\Delta y }_{\mathrm{Area}} = (\rho g) y_jf(y_j) \Delta y \]
The force \(F\) is approximated by a Riemann sum that converges to an integral: \[ F = F_1 + \cdots + F_N \approx \rho g\sum_{j=1}^N y_jf(y_j) \Delta y \quad \Rightarrow\quad F = \rho g \int_a^b y f(y)\, dy \]
THEOREM 1 Fluid Force on a Flat Surface Submerged Vertically
The fluid force \(F\) on a flat side of an object submerged vertically in a fluid is \[ F = \rho g \int_a^b y f(y)\, dy\tag{2} \]
where \(f(y)\) is the horizontal width of the side at depth \(y\), and the object extends from depth \(y=a\) to depth \(y=b\).
476
EXAMPLE 3
Calculate the fluid force \(F\) on one side of an equilateral triangular plate of side 2 m submerged vertically in a tank of oil of mass density \(\rho = 900 \text{kg/m}^3\) (Figure 8.15).
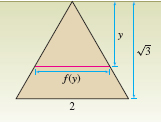
Solution To use Eq.(2), we need to find the horizontal width \(f(y)\) of the plate at depth \(y\). An equilateral triangle of side \(s = 2\) has height \(\sqrt 3 s/2 = \sqrt 3\). By similar triangles, \(y/f(y)=\sqrt 3/2\) and thus \(f(y) = 2y/\sqrt{3}\). By Eq.(2), \[ F = \rho g \int_0^{\sqrt 3} y\, f(y)\, dy = (900)(9.8) \int_0^{\sqrt 3} \frac{2}{\sqrt 3}y^2 \, dy = \left(\frac{17{,}640}{\sqrt 3}\right) \frac{y^3}{3}\bigg|_0^{\sqrt 3} = 17{,}640 \textrm{N} \]
The next example shows how to modify the force calculation when the side of the submerged object is inclined at an angle.
EXAMPLE 4 Force on an Inclined Surface
The side of a dam is inclined at an angle of \(45^\circ\). The dam has height 700 ft and width 1500 ft as in Figure 8.16. Calculate the force \(F\) on the dam if the reservoir is filled to the top of the dam. Water has density \(w = 62.5\) lb/ft\(^3\).

Solution The vertical height of the dam is 700 ft, so we divide the vertical axis from 0 to 700 into \(N\) subintervals of length \(\Delta y=700/N\). This divides the face of the dam into \(N\) strips as in Figure 8.16. By trigonometry, each strip has width equal to \(\Delta y/\sin(45^\circ) = \sqrt 2 \Delta y\). Therefore, \[ \textrm{Area of each strip} = \textrm{length}\times\textrm{width} = 1500(\sqrt 2\, \Delta y) \]
As usual, we approximate the force \(F_j\) on the \(j\)th strip. The factor \(\rho g\) is equal to weight per unit volume, so we use \(w = 62.5\) lb/ft\(^3\) in place of \(\rho g\): \[ \begin {eqnarray} F_j &\approx &\overbrace{wy_j}^{\textrm{Pressure}}\times \overbrace{1500\sqrt 2 \Delta y}^{\textrm{Area of strip}} = wy_j\times 1500\sqrt 2\,\Delta y\,\,\,\textrm{lb}\notag\\ F = \sum_{j = 1}^N F_j &\approx &\sum_{j = 1}^N wy_j\bigl(1500\sqrt 2 \,\Delta y\bigr) = 1500\sqrt 2\, w \sum_{j = 1}^N y_j \Delta y \notag \end {eqnarray} \]

477
This is a Riemann sum for the integral \({1500\sqrt 2 w\int_0^{700} y\,dy}\). Therefore, \[ F = 1500\sqrt 2 w\int_0^{700} y\, dy = 1500 \sqrt{2}(62.5)\frac{700^2}{2} \approx 3.25\times 10^{10} \textrm{lb} \]
8.2.1 Summary
- If pressure is constant, then force \(=\) pressure \(\times\) area.
- The fluid pressure at depth \(h\) is equal to \(\rho gh\), where \(\rho\) is the fluid density (mass per unit volume) and \(g=9.8 \text{m/s}^2\) is the acceleration due to gravity. Fluid pressure acts on a surface in the direction perpendicular to the surface. Water has mass density \(1000 \text{kg/m}^3\).
- If an object is submerged vertically in a fluid and extends from depth \(y=a\) to \(y=b\), then the total fluid force on a side of the object is \[ F = \rho g \int_a^b y f(y)\, dy \] where \(f(y)\) is the horizontal width of the side at depth \(y\).
- If fluid density is given as weight per unit volume, the factor \(g\) does not appear. Water has weight density 62.5 lb/ft\(^3\).