8.3 Center of Mass
Every object has a balance point called the center of mass (Figure 8.17). When a rigid object such as a hammer is tossed in the air, it may rotate in a complicated fashion, but its center of mass follows the same simple parabolic trajectory as a stone tossed in the air. In this section we use integration to compute the center of mass of a thin plate (also called a lamina of constant mass density \(\rho\).
The center of mass (COM) is expressed in terms of quantities called moments. The moment of a single particle of mass \(m\) with respect to a line \(L\) is the product of the particle's mass \(m\) and its directed distance (positive or negative) to the line: \[ \textrm{Moment with respect to line}~L = m \times \textrm{directed distance to}~L \]

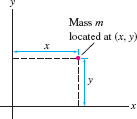
The particular moments with respect to the \(x\)- and \(y\)-axes are denoted \(M_x\) and \(M_y\). For a particle located at the point \((x,y)\) (Figure 8.18), \[ \begin{align*} M_x = my\qquad(\textrm{mass times directed distance to} x\textrm{-axis}) \\ M_y = mx\qquad(\textrm{mass times directed distance to} y\textrm{-axis}) \end{align*} \]
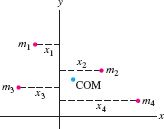
By definition, moments are additive: the moment of a system of \(n\) particles with coordinates \((x_j,y_j)\) and mass \(m_j\) (Figure 8.19) is the sum \[ \begin{align*} M_x = m_1y_1 + m_2y_2 + \cdots + m_ny_n \\ M_y = m_1x_1 + m_2x_2 + \cdots + m_nx_n \end{align*} \]
CAUTION
The notation is potentially confusing: \(M_x\) is defined in terms of \(y\)-coordinates and \(M_y\) in terms of \(x\)-coordinates.
The center of mass (COM) is the point \(P = (x_{\mathrm{CM}}, y_{\mathrm{CM}})\) with coordinates \[ \boxed{\bbox[#FAF8ED,5pt]{x_{\mathrm{CM}} = \frac{M_y }{M }, \qquad y_{\mathrm{CM}} = \frac{M_x}{M}}} \]
where \(M = m_1 + m_2+ \cdots + m_n\) is the total mass of the system.
EXAMPLE 1
Find the COM of the system of three particles in Figure 8.20, having masses 2, 4, and 8 at locations \((0,2)\), \((3,1)\), and \((6,4)\).
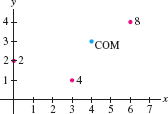
Solution The total mass is \(M = 2+4+8 = 14\) and the moments are \[ \begin{align*} M_x = m_1y_1+m_2y_2+m_3y_3 = 2\cdot 2 + 4\cdot 1 + 8\cdot 4 = 40 \\ M_y = m_1x_1+m_2x_2+m_3x_3 = 2\cdot 0 + 4\cdot 3 + 8\cdot 6 = 60 \end{align*} \]
Therefore, \( x_{\mathrm{CM}} = \tfrac{60}{14}=\tfrac{30}{7}\) and \(y_{\mathrm{CM}} = \tfrac{40}{14}=\tfrac{20}{7}\). The COM is \(\big(\frac{30}7,\frac{20}7\big)\).
481
Laminas (Thin Plates)
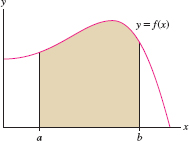
Now consider a lamina (thin plate) of constant mass density \(\rho\) occupying the region under the graph of \(f(x)\) over an interval \([a,b]\), where \(f(x)\) is continuous and \(f(x)\ge 0\) (Figure 8.21). In our calculations we will use the principle of additivity of moments mentioned above for point masses:
If a region is decomposed into smaller, non-overlapping regions, then the moment of the region is the sum of the moments of the smaller regions.
In this section, we restrict our attention to thin plates of constant mass density (also called “uniform density”). COM computations when mass density is not constant require multiple integration and are covered in Section 15.5.
To compute the \(y\)-moment \(M_y\), we begin as usual, by dividing \([a,b]\) into \(N\) subintervals of width \(\Delta x = ({b-a})/{N}\) and endpoints \(x_j=a+j\Delta x\). This divides the lamina into \(N\) vertical strips (Figure 8.22). If \(\Delta x\) is small, the \(j\)th strip is nearly rectangular of area \(f(x_j) \Delta x\) and mass \(\rho f(x_j) \Delta x\). Since all points in the strip lie at approximately the same distance \(x_j\) from the \(y\)-axis, the moment \(M_{y,j}\) of the \(j\)th strip is approximately \[ M_{y,j}\approx (\textrm{mass}) \times (\textrm{directed distance to \(y\)-axis}) = (\rho f(x_j) \Delta x) x_j \]
By additivity of moments, \[ M_y = \sum_{j = 1}^N M_{y,j} \approx \rho\sum_{j = 1}^N x_jf(x_j) \Delta x \]
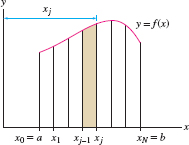
This is a Riemann sum whose value approaches \( \rho \int_a^b xf(x)\, dx\) as \(N\to \infty\), and thus \[ \boxed{\bbox[#FAF8ED,5pt]{ M_y = \rho \int_a^b x f(x)\, dx}} \]
More generally, if the lamina occupies the region between the graphs of two functions \(f_1(x)\) and \(f_2(x)\) over \([a,b]\), where \(f_1(x)\ge f_2(x)\), then \[ \boxed{\bbox[#FAF8ED,5pt]{M_y = \rho \int_a^b x (\textrm{length of vertical cut})\, dx = \rho \int_a^b x \bigl(f_1(x)-f_2(x)\bigr)\, dx}}\tag{1} \]
Think of the lamina as made up of vertical strips of length \(f_1(x)-f_2(x)\) at distance \(x\) from the \(y\)-axis (Figure 8.23).

482
We can compute the \(x\)-moment by dividing the lamina into horizontal strips, but this requires us to describe the lamina as a region between two curves \(x = g_1(y)\) and \(x = g_2(y)\) with \(g_1(y) \geq g_2(y)\) over an interval \([c,d]\) along the \(y\)-axis (Figure 8.24): \[ \boxed{\bbox[#FAF8ED,5pt]{M_x = \rho \int_c^d y (\textrm{length of horizontal cut})\, dy = \rho \int_c^d y \bigl(g_1(y)-g_2(y)\bigr)\, dy}}\tag{2} \]
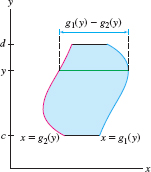
The total mass of the lamina is \(M = \rho A\), where \(A\) is the area of the lamina: \[ \boxed{\bbox[#FAF8ED,5pt]{M = \rho A = \rho \int_a^b \bigl(f_1(x)-f_2(x)\bigr)\,dx\qquad\hbox{or}\qquad \rho\int_c^d \bigl(g_1(y)-g_2(y)\bigr)\, dy}} \]
The center-of-mass coordinates are the moments divided by the total mass: \[ \boxed{\bbox[#FAF8ED,5pt]{ x_{\mathrm{CM}} = \frac{M_y}{M}, \qquad y_{\mathrm{CM}} = \frac{M_x}{M} }} \]
EXAMPLE 2
Find the moments and COM of the lamina of uniform density \(\rho\) occupying the region underneath the graph of \(f(x) = x^2\) for \(0\le x \le 2\).
Solution First, compute \(M_y\) using Eq. (1): \[ M_y = \rho\int_0^2 x f(x) \, dx = \rho\int_0^2 x (x^2) \, dx = \rho\,\frac{x^4}4\bigg|_0^2 = 4\rho \]
Then compute \(M_x\) using Eq. (2), describing the lamina as the region between \(x= \sqrt y\) and \(x =2\) over the interval \([0,4]\) along the \(y\)-axis (Eq. (2), \[ \begin {eqnarray} M_x &=& \rho\int_0^4 y\bigl(g_1(y)-g_2(y)\bigr)\, dy = \rho\int_0^4 y(2-\sqrt y)\, dy\notag\\ &=& \rho \left(y^2-\frac25y^{5/2}\right)\bigg|_0^4 = \rho \left(16-\frac25\cdot 32 \right) = \frac{16}5 \rho \notag \end {eqnarray} \]
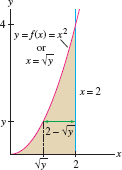
The plate has area \(A = \int_0^2 x^2\, dx = \tfrac{8}{3}\) and total mass \(M = \frac{8}{3}\rho\). Therefore, \[ x_{\mathrm{CM}} = \frac{M_y}{M} = \frac{4\rho}{\frac83\rho} = \frac{3}{2},\qquad y_{\mathrm{CM}} = \frac{M_x}{M} = \frac{\frac{16}5\rho}{\frac83\rho} = \frac65 \]
CONCEPTUAL INSIGHT
The COM of a lamina of constant mass density \(\rho\) is also called the centroid. The centroid depends on the shape of the lamina, but not on its mass density because the factor \(\rho\) cancels in the ratios \(M_x/M\) and \(M_y/M\). In particular, in calculating the centroid, we can take \(\rho =1\). When mass density is not constant, the COM depends on both shape and mass density. In this case, the COM is computed using multiple integration (Section 15.5).
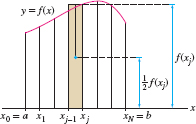
A drawback of Eq. (2) for \(M_x\) is that it requires integration along the \(y\)-axis. Fortunately, there is a second formula for \(M_x\) as an integral along the \(x\)-axis. As before, divide the region into \(N\) thin vertical strips of width \(\Delta x\) (see Figure 8.26). Let \(M_{x,j}\) be the \(x\)-moment of the \(j\)th strip and let \(m_j\) be its mass. We can use the following trick to approximate \(M_{x,j}\). The strip is nearly rectangular with height \(f(x_j)\) and width \(\Delta x\), so \(m_j\approx \rho f(x_j)\,\Delta x\). Furthermore, \(M_{x,j} = y_j m_j\), where \(y_j\) is the \(y\)-coordinate of the COM of the strip. However, \(y_j\approx \frac12 f(x_j)\) because the COM of a rectangle is located at its center. Thus, \[ \begin{align*} & M_{x,j}= m_jy_j \approx\rho f(x_j)\Delta x\cdot \frac12f(x_j) = \frac12\rho f(x_j)^2\Delta x\\ & M_x =\sum_{j=1}^N M_{x,j}\approx \frac12\rho\sum_{j = 1}^N f(x_j)^2 \Delta x \end{align*} \]
483
This is a Riemann sum whose value approaches \({\frac{1}{2} \rho \int_a^b f(x)^2\, dx}\) as \(N\to\infty\). The case of a region between the graphs of functions \(f_1(x)\) and \(f_2(x)\) where \(f_1(x)\ge f_2(x)\ge 0\) is treated similarly, so we obtain the alternative formulas \[ \boxed{\bbox[#FAF8ED,5pt]{M_x = \frac{1}{2} \rho \int_a^b f(x)^2\, dx \qquad \textrm{or}\qquad \frac{1}{2} \rho \int_a^b \bigl(f_1(x)^2-f_2(x)^2\bigr)\, dx}}\tag{3} \]
EXAMPLE 3
Find the centroid of the shaded region in Figure 8.27.
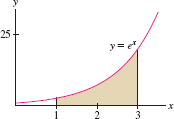
Solution The centroid does not depend on \(\rho\), so we may set \(\rho = 1\) and apply Eqs.(1) and (3) with \(f(x)=e^x\): \[ M_x = \frac12 \int_1^3 f(x)^2\, dx = \frac12 \int_1^3 e^{2x} \, dx = \frac14\,e^{2x}\bigg|_1^3 = \frac{e^6 - e^2}4\ \]
Using Integration by Parts, \[ M_y = \int_1^3 x f(x)\, dx = \int_1^3 x e^x\, dx = (x-1)e^x \bigg|_1^3 = 2e^3 \]
The total mass is \(M = \displaystyle\int_1^3 e^x\, dx = (e^3 - e)\). The centroid has coordinates \[ x_{\mathrm{CM}} = \frac{M_y}{M}=\frac{2e^3}{e^3 - e} \approx 2.313,\qquad y_{\mathrm{CM}} = \frac{M_x}{M} =\frac{e^6 - e^2}{4(e^3 - e)}\approx 5.701 \]
The symmetry properties of an object give information about its centroid (Figure 8.28). For instance, the centroid of a square or circular plate is located at its center. Here is a precise formulation (see Exercise 43).
THEROEM 1 Symmetry Principle
If a lamina is symmetric with respect to a line, then its centroid lies on that line.
EXAMPLE 4 Using Symmetry
Find the centroid of a semicircle of radius 3.
Solution Symmetry cuts our work in half. The semicircle is symmetric with respect to the \(y\)-axis, so the centroid lies on the \(y\)-axis, and hence \(x_{\mathrm{CM}} = 0\). It remains to calculate \(M_x\) and \(y_{\mathrm{CM}}\). The semicircle is the graph of \(f(x) =\sqrt{9-x^2}\) (Figure 8.29). By Eq.(3) with \(\rho = 1\), \[ M_x = \frac12\int_{-3}^3 f(x)^2\,dx = \frac12\int_{-3}^3 (9-x^2) \,dx = \frac12\left(9x-\frac13x^3\right)\bigg|_{-3}^3 = 9 - (-9)=18 \]
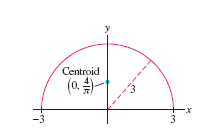
The semicircle has area (and mass) equal to \(A = \frac12 \pi(3^2)=9\pi/2\), so \[ y_{\mathrm{CM}} = \frac{M_x}{M} = \frac{18}{9\pi/2} = \frac{4}{\pi} \approx 1.27\]
484
EXAMPLE 5 Using Additivity and Symmetry
Find the centroid of the region \(R\) in Figure 8.30.
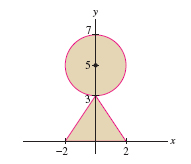
Solution We set \(\rho =1\) because we are computing a centroid. The region \(R\) is symmetric with respect to the \(y\)-axis, so we know in advance that \(x_{\mathrm{CM}}=0\). To find \(y_{\mathrm{CM}}\), we compute the moment \(M_x\).
Step 1. Use additivity of moments.
Let \(M_x^{\textrm{triangle}}\) and \(M_x^{\textrm{circle}}\) be the \(x\)-moments of the triangle and the circle. Then \[ M_x = M_x^{\textrm{triangle}} + M_x^{\textrm{circle}} \]
Step 2. Moment of the circle.
To save work, we use the fact that the centroid of the circle is located at the center \((0,5)\) by symmetry. Thus \(y_{\mathrm{CM}}^{\mathrm{circle}} = 5\) and we can solve for the moment: \[ y_{\mathrm{CM}}^{\textrm{circle}} = \frac{M_x^{\textrm{circle}}}{M^{\textrm{circle}}} = \frac{M_x^{\textrm{circle}}}{4\pi} = 5\quad \Rightarrow\quad M_x^{\textrm{circle}} = 20\pi \]
Here, the mass of the circle is its area \(M^{\textrm{circle}} = \pi(2^2)=4\pi\) (since \(\rho =1\)).
Step 3. Moment of a triangle.
Let's compute \(M_x^{\textrm{triangle}}\) for an arbitrary triangle of height \(h\) and base \(b\) (Figure 8.31). Let \(\ell(y)\) be the width of the triangle at height \(y\). By similar triangles, \[ \dfrac{\ell(y)}{h-y} = \dfrac{b}{h}\quad\Rightarrow\quad \ell(y) = b-\frac{b}{h}y \]
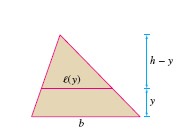
By Eq. (2), \[ M_x^{\textrm{triangle}} = \int_0^h y\ell(y)\,dy= \int_0^h y\left(b-\frac{b}hy\right) dy = \left(\frac{by^2}{2}-\frac{by^3}{3h}\right)\bigg|_0^h=\frac{bh^2}{6} \]
In our case, \(b=4\), \(h=3\), and \( M_x^{\textrm{triangle}}=\dfrac{4\cdot 3^2}{6}=6. \)
Step 4. Computation of \(y_{\mathrm{CM}}\). \[ M_x = M_x^{\textrm{triangle}} + M_x^{\textrm{circle}} = 6+20\pi \]
The triangle has mass \(\frac12\cdot 4\cdot 3 = 6\), and the circle has mass \(4\pi\), so \(R\) has mass \(M = 6 + 4\pi\) and \[ y_{\mathrm{CM}} = \frac{M_x}{M} = \frac{6+20\pi}{6+4\pi} \approx 3.71 \]
8.3.1 Summary
- The moments of a system of particles of mass \(m_j\) located at \((x_j,y_j)\) are
\[
M_x = m_1y_1 + \cdots + m_ny_n,\qquad M_y = m_1x_1 + \cdots +
m_nx_n
\]
The center of mass (COM) has coordinates \[ x_{\mathrm{CM}} = \dfrac{M_y}{M}\qquad\hbox{and}\qquad y_{\mathrm{CM}} = \dfrac{M_x}{M} \]
where \(M = m_1 +\cdots + m_n\).
485
- Lamina (thin plate) of constant mass density \(\rho\) (region under the graph of \(f(x)\) where \(f(x)\ge 0\), or between the graphs of \(f_1(x)\) and \(f_2(x)\) where \(f_1(x)\ge f_2(x)\)): \[ M_y = \rho \int_a^b x f(x) \, dx \qquad \textrm{or}\qquad \rho \int_a^b x \bigl(f_1(x)-f_2(x)\bigr)\, dx \]
- There are two ways to compute the \(x\)-moment \(M_x\). If the lamina occupies the region between the graph of \(x = g(y)\) and the \(y\)-axis where \(g(y)\ge 0\), or between the graphs of \(g_1(y)\) and \(g_2(y)\) where \(g_1(y)\ge g_2(y)\), then \[ M_x = \rho \int_c^d y g(y) \, dy \qquad \textrm{or}\qquad \rho \int_c^d y \bigl(g_1(y)-g_2(y)\bigr)\, dy \]
- Alternative (often more convenient) formula for \(M_x\): \[ M_x = \frac{1}{2}\rho \int_a^b f(x)^2\, dx\qquad \textrm{or}\qquad \frac{1}{2} \rho \int_a^b \bigl(f_1(x)^2-f_2(x)^2\bigr)\, dx \]
- The total mass of the lamina is \( M = \rho\int_a^b \bigl(f_1(x)-f_2(x)\bigr)\, dx\). The coordinates of the center of mass (also called the centroid) are \[ x_{\mathrm{CM}} = \frac{M_y}{M},\qquad y_{\mathrm{CM}} = \frac{M_x}{M} \]
- Additivity: If a region is decomposed into smaller non-overlapping regions, then the moment of the region is the sum of the moments of the smaller regions.
- Symmetry Principle: If a lamina of constant mass density is symmetric with respect to a given line, then the center of mass (centroid) lies on that line.
Historical Perspective

We take it for granted that physical laws are best expressed as mathematical relationships. Think of \(F = ma\) or the universal law of gravitation. However, the fundamental insight that mathematics could be used to formulate laws of nature (and not just for counting or measuring) developed gradually, beginning with the philosophers of ancient Greece and culminating some 2000 years later in the discoveries of Galileo and Newton. Archimedes (287-212 BCE) was one of the first scientists (perhaps the first) to formulate a precise physical law. Concerning the principle of the lever, Archimedes wrote, “Commensurable magnitudes balance at distances reciprocally proportional to their weight.” In other words, if weights of mass \(m_1\) and \(m_2\) are placed on a weightless lever at distances \(L_1\) and \(L_2\) from the fulcrum \(P\) (Figure 8.32), then the lever will balance if \(m_1/m_2=L_2/L_1\), or \[ \boxed{\bbox[#FAF8ED,5pt]{ m_1 L_1 = m_2 L_2 }} \]
In our terminology, what Archimedes had discovered was the center of mass \(P\) of the system of weights (see Exercises 41 and 42).