9.2 Models Involving \(y' = k (y - b)\)
Every first-order, linear differential equation with constant coefficients can be written in the form of Eq. (1). This equation is used to model a variety of phenomena, such as the cooling process, free-fall with air resistance, and current in a circuit.
We have seen that a quantity grows or decays exponentially if its rate of change is proportional to the amount present. This characteristic property is expressed by the differential equation \(y' = ky\). We now study the closely related differential equation \[ \begin{equation}\label{models.basiceq} \boxed{\bbox[#FAF8ED,5pt]{\frac{dy}{dt} = k(y - b)}}\tag {1} \end{equation}\] where \(k\) and \(b\) are constants and \(k\ne 0\). This differential equation describes a quantity \(y\) whose rate of change is proportional to the difference \(y-b\). We can use separation of variables to show that solution is \[ \begin{equation}\label{models.soltheorem} \boxed{\bbox[#FAF8ED,5pt]{y(t) = b + Ce^{kt}}}\tag {2} \end{equation} \] Alternatively, we may observe that \((y - b)' = y'\) since \(b\) is a constant, so Eq. (1) may be rewritten \[ \frac{d}{dt}(y - b) = k(y - b) \] In other words, \(y-b\) satisfies the differential equation of an exponential function and thus \(y-b = Ce^{kt}\), or \(y = b + Ce^{kt}\), as claimed.
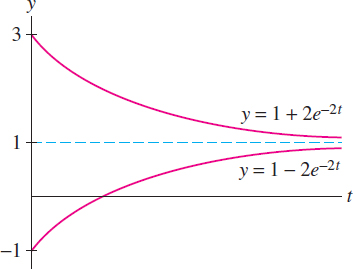
GRAPHICAL INSIGHT
The behavior of the solution \(y(t)\) as \(t \to \infty\) depends on whether \(C\) and \(k\) are positive or negative. When \(k>0\), \(e^{kt}\) tends to \(\infty\) and therefore, \(y(t)\) tends to \(\infty\) if \(C > 0\) and to \(-\infty\) if \(C < 0\). When \(k<0 \), we usually rewrite the differential equation as \(y'=-k(y-b)\) with \(k > 0 \). In this case, \(y(t)=b+Ce^{-kt}\) and \(y(t)\) approaches the horizontal asymptote \(y=b\) since \(Ce^{-kt}\) tends to zero as \(t\to\infty\) (Figure 9.7). However, \(y(t)\) approaches the asymptote from above or below, depending on whether \(C>0\) or \(C < 0\).
Newton's Law of Cooling implies that the object cools quickly when it is much hotter than its surroundings (when \(y-T_0\) is large). The rate of cooling slows as \(y\) approaches \(T_0\). When the object's initial temperature is less than \(T_0\), \(y'\) is positive and Newton's Law models warming.
We now consider some applications of Eq. (1), beginning with Newton's Law of Cooling. Let \(y(t)\) be the temperature of a hot object that is cooling off in an environment where the ambient temperature is \(T_0\). Newton assumed that the rate of cooling is proportional to the temperature difference \(y-T_0\). We express this hypothesis in a precise way by the differential equation \[\boxed{\bbox[#FAF8ED,5pt]{y'=-k(y-T_0)\qquad\quad\textrm{(\(T_0 =\) ambient temperature)}}}\] The constant \(k\), in units of \(\mathrm{(time)}^{-1}\), is called the cooling constant and depends on the physical properties of the object.
512
Reminder
The differential equation \[\frac{dy}{dt} = k(y - b)\] has general solution \[y=b + Ce^{kt}\]
EXAMPLE 1 Newton's Law of Cooling
A hot metal bar with cooling constant \(k = 2.1 \mathrm{min}^{-1}\) is submerged in a large tank of water held at temperature \(T_0 = 10^\circ\mathrm{C}\). Let \(y(t)\) be the bar's temperature at time \(t\) (in minutes).
- Find the differential equation satisfied by \(y(t)\) and find its general solution.
- What is the bar's temperature after 1 min if its initial temperature was \(180^\circ\mathrm{C}\)?
- What was the bar's initial temperature if it cooled to \(80^\circ\mathrm{C}\) in 30 s?
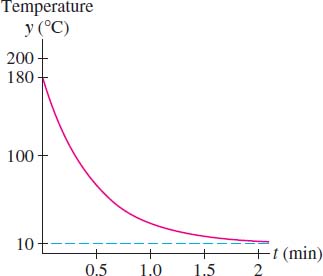
Solution
(a) Since \(k = 2.1 \mathrm{min}^{-1}\), \(y(t)\) (with \(t\) in minutes) satisfies \[ y' = -2.1(y - 10) \] By Eq. (2), the general solution is \(y(t) = 10 + Ce^{-2.1t}\) for some constant \(C\).
(b) If the initial temperature was \(180^\circ\mathrm{C}\), then \(y(0) = 10 +C =180\). Thus, \(C = 170\) and \(y(t) = 10 + 170e^{-2.1t}\) (Figure 9.8). After 1 min, \[ y(1) = 10+170e^{-2.1(1)} \approx 30.8^\circ\mathrm{C} \]
(c) If the temperature after 30 s is \(80^\circ\mathrm{C}\), then \(y(0.5) = 80\), and we have \[ \begin{align*} 10 + Ce^{-2.1(0.5)} &= 80\quad \Rightarrow\quad Ce^{-1.05} = 70\quad \Rightarrow\quad C = 70 e^{1.05}\approx 200 \end{align*}\] It follows that \(y(t) = 10 + 200e^{-2.1t}\) and the initial temperature was \[ y(0) = 10 + 200e^{-2.1(0)} = 10 + 200 = 210^\circ\mathrm{C} \]
The effect of air resistance depends on the physical situation. A high-speed bullet is affected differently than a skydiver. Our model is fairly realistic for a large object such as a skydiver falling from high altitudes.
The differential equation \(y' = k(y - b)\) is also used to model free-fall when air resistance is taken into account. Assume that the force due to air resistance is proportional to the velocity \(v\) and acts opposite to the direction of the fall. We write this force as \(-kv\), where \(k > 0\). We take the upward direction to be positive, so \(v<0\) for a falling object and \(-kv\) is an upward acting force.
The force due to gravity on a falling object of mass \(m\) is \(- mg\), where \(g\) is the acceleration due to gravity, so the total force is \(F = - mg - kv\). By Newton's Law, \[F = ma = mv'\qquad \text{(\(a =v'\) is the acceleration)}\] Thus \(mv' = - mg-kv\), which can be written \[ \begin{equation}\label{9.2.freefallmodel} \boxed{\bbox[#FAF8ED,5pt]{v' = -\frac{k}{m} \left(v + \frac{mg}{k}\right)}}\tag {3} \end{equation}\]
In this model of free fall, \(k\) has units of mass per time, such as kg/s.
This equation has the form \(v' = -k(v - b)\) with \(k\) replaced by \(k/m\) and \(b=-mg/k\). By Eq. (2) the general solution is \[\begin{equation} v(t) = -\frac{mg}{k} + Ce^{-({k}/{m})t}\tag {4} \end{equation}\] Since \(Ce^{-({k}/{m})t}\) tends to zero as \(t\to \infty\), \(v(t)\) tends to a limiting terminal velocity: \[\begin{equation} \textrm{Terminal velocity} = \lim_{t\to\infty} v(t) = -\frac{mg}{k}\tag {5} \end{equation}\] Without air resistance the velocity would increase indefinitely.
513
EXAMPLE 2
An 80-kg skydiver steps out of an airplane.
- What is her terminal velocity if \(k = 8 \text{kg/s}\)?
- What is her velocity after 30 s?
Solution
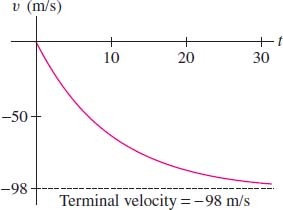
- By Eq. (5), with \(k=8 \text{kg/s}\) and \(g = 9.8 \text{m/s}^2\), the terminal velocity is \[ -\frac{mg}{k} = -\frac{(80)9.8}{8} = -98 \text{m/s} \]
- With \(t\) in seconds, we have, by Eq. (4), \[ v(t) = -98 + Ce^{-(k/m)t} = -98 + Ce^{-({8}/{80})t} = -98 + Ce^{-0.1t} \]
We assume that the skydiver leaves the airplane with no initial vertical velocity, so \(v(0)=-98+C=0\), and \(C=98\). Thus we have \(v(t) = -98(1-e^{-0.1t})\) [Figure 9.9]. The skydiver's velocity after 30 s is \[ v(30)=-98(1-e^{-0.1(30)})\approx -93.1 \text{m/s} \]

Notice in Eq. (6) that \(P'(t)\) is determined by the growth rate \(r\) and the withdrawal rate \(N\!\). If no withdrawals occurred, \(P(t)\) would grow with compound interest and would satisfy \(P'(t) = rP(t)\).
An annuity is an investment in which a principal \(P_0\) is placed in an account that earns interest (compounded continuously) at a rate \(r\), and money is withdrawn at regular intervals. To model an annuity by a differential equation, we assume that the money is withdrawn continuously at a rate of \(N \text{dollars per year}\). Let \(P(t)\) be the balance in the annuity after \(t\) years. Then \[ \begin{equation} \label{7.models.annuityeqn} \underbrace{P'(t)}_{\mbox{\(\begin{array}{@{}c@{}}\textrm{Rate of}\\ \textrm{change}\end{array}\)}} = \underbrace{rP(t)}_{\mbox{\(\begin{array}{@{}c@{}}\textrm{Growth due}\\ \textrm{to interest}\end{array}\)}} - \underbrace{\phantom{(}N\phantom{)}}_{\mbox{\(\begin{array}{@{}c@{}}\textrm{Withdrawal}\\ \textrm{rate}\end{array}\)}} = r \left(P(t) - \frac{N}{r} \right)\tag {6} \end{equation} \] This equation has the form \(y'=k(y-b)\) with \(k=r\) and \(b=N/r\), so by Eq. (2), the general solution is \[ \begin{equation} P(t) = \frac{N}r + Ce^{rt} \label{7.models.annuityformula} \tag {7} \end{equation} \] Since \(e^{rt}\) tends to infinity as \(t\to\infty\), the balance \(P(t)\) tends to \(\infty\) if \(C>0\). If \(C<0\), then \(P(t)\) tends to \(-\infty\) (i.e., the annuity eventually runs out of money). If \(C=0\), then \(P(t)\) remains constant with value \(N/r\).
EXAMPLE 3 Does an Annuity Pay Out Forever?
An annuity earns interest at the rate \(r = 0.07\), and withdrawals are made continuously at a rate of \(N=\$500\text{/year}\).
- When will the annuity run out of money if the initial deposit is \(P(0)=\$5000\)?
- Show that the balance increases indefinitely if \(P(0)=\$9000\).
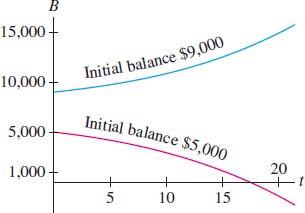
Solution We have \({N}/{r}=\tfrac{500}{0.07}\approx 7143\), so \(P(t)=7143+Ce^{0.07t}\) by Eq. (7).
- If \(P(0)=5000=7143+Ce^0\), then \(C=-2143\) and
\[
P(t) = 7143-2143e^{0.07t}
\]
The account runs out of money when \(P(t)=7143-2143e^{0.07t}=0\), or
\[
e^{0.07t}=\frac{7143}{2143}\quad\Rightarrow\quad 0.07t =
\ln\left(\frac{7143}{2143}\right) \approx 1.2
\]
The annuity money runs out at time \(t=\tfrac{1.2}{0.07}\approx 17\) years.
514
- If \(P(0)=9000=7143+Ce^0\), then \(C= 1857\) and \[ P(t) = 7143+1857e^{0.07t} \]
Since the coefficient \(C=1857\) is positive, the account never runs out of money. In fact, \(P(t)\) increases indefinitely as \(t\to\infty\). Figure 9.10 illustrates the two cases.
9.2.1 Summary
- The general solution of \(y' = k(y - b)\) is \(y = b + Ce^{kt}\), where \(C\) is a constant.
- The following tables describe the solutions to \(y'=k(y-b)\)
(see Figure 9.11).
Equation (\(k>0\)) Solution Behavior as \(t\to\infty\) \(y'=k(y-b)\) \(y(t)=b+Ce^{kt}\) \[{ \lim_{t\to\infty}y(t) = \left\{\begin{array}{@{}ll@{}} \infty & \textrm{if \(C>0\)} \\ -\infty & \textrm{if \(C<0\)} \\ \end{array} \right. }\] \(y'=-k(y-b)\) \(y(t)=b+Ce^{-kt}\) \[ \lim_{t\to\infty}y(t) =b\] 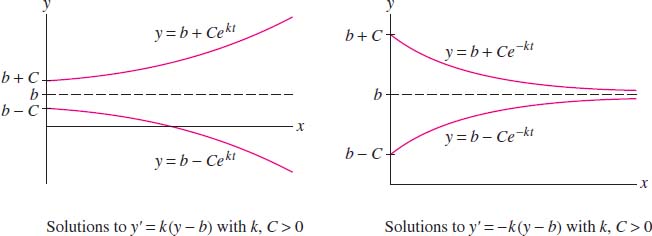
- Three applications:
- - Newton's law of cooling: \(y'=-k(y-T_0)\), \(y(t)=\) temperature of the object, \(T_0 = \) ambient temperature, \(k= \) cooling constant
- - Free-fall with air resistance: \(v' = -\frac{k}m\left(v+\frac{mg}k\right)\), \(v(t) =\) velocity, \(m =\) mass, \(k =\) air resistance constant, \(g =\) acceleration due to gravity
- - Continuous annuity: \(P'=r\left(P-\frac{N}r\right)\), \(P(t) =\) balance in the annuity, \(r = \) interest rate, \(N = \) withdrawal rate