In the formula for the integrating factor \(\alpha(x)\), the integral \(\int A(x)\,dx\) denotes any antiderivative of \(A(x)\).

THEOREM 1

The general solution of \(y'+A(x)y=B(x)\) is \[ \begin{equation} \label{10.firstord.genformula} \boxed{\bbox[#FAF8ED,5pt]{y = \frac1{\alpha(x)}\left(\int \alpha(x)B(x)\,dx + C \right)}} \tag {4} \end{equation} \] where \(\alpha(x)\) is an integrating factor: \[ \begin{equation} \label{10.firstord.formintfactor} \boxed{\bbox[#FAF8ED,5pt]{\alpha(x) = e^{\int A(x)\,dx}}} \tag {5} \end{equation} \]

EXAMPLE 1

Solve \(xy'-3y= x^{2}\), \(y(1) = 2\).

Solution First divide by \(x\) to put the equation in the form \(y'+A(x)y=B(x)\): \[ y'-\frac{3}{x}\ y = x\qquad \] Thus \(A(x)=-3x^{-1}\) and \(B(x)=x\).

Step 1. Find an integrating factor

In our case, \(A(x)=-3x^{-1}\), and by Eq. (5), \[ \alpha(x) = e^{\int A(x)\,dx} = e^{\int (-3/{x})\,dx} = e^{-3\ln x} = e^{\ln(x^{-3})}=x^{-3} \]

Step 2. Find the general solution

We have found \(\alpha(x)\), so we can use Eq. (4) to write down the general solution: \[ \begin{align} y&= \alpha(x)^{-1}\int \alpha(x)B(x)\,dx = x^3\left(\int x^{-3}\cdot x\, dx\right)\notag \\ &=x^3\left(\int x^{-2}\, dx\right) =x^3\left(-x^{-1}+C\right) \tag {6}\\ &\boxed{\bbox[#FAF8ED,5pt]{y = -x^2+Cx^3}}\nonumber \end{align} \]

Step 3. Solve the initial value problem.

Now solve for \(C\) using the initial condition \(y(1)=2\): \[ y(1) = -1^2+C\cdot 1^3=2\qquad\textrm{or}\qquad C=3 \] Therefore, the solution of the initial value problem is \(y = -x^2 + 3\,x^3\).

Finally, let's check that \(y = -x^2 + 3x^3\) satisfies our equation \(xy'-3y= x^{2}\): \[ \begin{align*} xy'-3y &= x(-2x+9x^2)-3(-x^2 + 3x^3)\\ & = (-2x^2+9x^3)+(3x^2-9x^3)=x^2 \end{align*} \]

EXAMPLE 2

Solve the initial value problem: \(y'+ (1-x^{-1})y= x^2\), \(y(1) = 2\).

Solution This equation has the form \(y'+A(x)y=B(x)\) with \(A(x)=(1-x^{-1})\). By Eq. (5), an integrating factor is \[ \alpha(x)=e^{\int(1-x^{-1})\,dx} = e^{x-\ln x}=e^xe^{\ln x^{-1}} = x^{-1}e^x \]

Using Eq. (4) with \(B(x)=x^2\), we obtain the general solution: \[ \begin{align*} y &= \alpha(x)^{-1}\left(\int \alpha(x)B(x)\,dx +C\right)= xe^{-x} \left(\int (x^{-1}e^x)x^2\,dx+C \right)\\ & = xe^{-x} \left(\int xe^x\,dx+C \right) \end{align*} \]

Integration by Parts shows that \(\int xe^x\,dx=(x-1)e^x+C\), so we obtain \[ y = xe^{-x}\big((x-1)e^x+C\big) = x(x-1)+Cxe^{-x} \]

The initial condition \(y(1)=2\) gives \[ y(1)= 1(1-1)+Ce^{-1} = Ce^{-1} =2\quad\Rightarrow\quad C=2e \]

The desired particular solution is \[ y = x(x-1)+(2e)xe^{-x} = x(x-1)+2xe^{1-x} \]

CONCEPTUAL INSIGHT

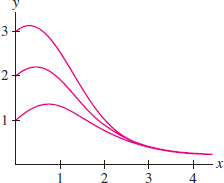
We have expressed the general solution of a first-order linear differential equation in terms of the integrals in Eqs. (4) and (5). Keep in mind, however, that it is not always possible to evaluate these integrals explicitly. For example, the general solution of \(y'+xy= 1\) is \[ y = e^{- x^2/2} \left(\int e^{x^2/2}\,dx + C \right) \] The integral \(\int e^{x^2/2}\,dx\) cannot be evaluated in elementary terms. However, we can approximate the integral numerically and plot the solutions by computer (Figure 9.25).

EXAMPLE 3 A Mixing Problem

A tank contains 600 liters of water with a sucrose concentration of \(0.2 \text{kg/L}\). We begin adding water with a sucrose concentration of \(0.1 \text{kg/L}\) at a rate of \(R_{\mathrm{in}} = 40 \text{L/min}\) (Figure 9.26). The water mixes instantaneously and exits the bottom of the tank at a rate of \(R_{\mathrm{out}} = 20 \text{L/min}\). Let \(y(t)\) be the quantity of sucrose in the tank at time \(t\) (in minutes). Set up a differential equation for \(y(t)\) and solve for \(y(t)\).

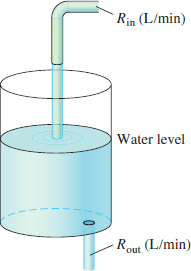
Solution

Step 1. Set up the differential equation

The derivative \({dy}/dt\) is the difference of two rates of change, namely the rate at which sucrose enters the tank and the rate at which it leaves: \[ \begin{equation} \label{10.firstord.rateinout} \frac{dy}{dt} = \textrm{sucrose rate in} - \textrm{sucrose rate out} \tag {7} \end{equation} \] The rate at which sucrose enters the tank is \[ \textrm{Sucrose rate in} = \underbrace{(0.1 \text{kg/L}) (40 \text{L/min})}_{\text{Concentration times water rate in}} = 4 \text{kg/min} \]

Next, we compute the sucrose concentration in the tank at time \(t\). Water flows in at \(40 \text{L/min}\) and out at \(20 \text{L/min}\), so there is a net inflow of \(20 \text{L/min}\). The tank has 600 L at time \(t=0\), so it has \(600+20t\) liters at time \(t\), and \[ \textrm{Concentration at time \(t\)} = \frac{\textrm{kilograms of sucrose in tank}}{\textrm{liters of water in tank}} = \frac{y(t)}{600+20t} \text{kg/L} \] The rate at which sucrose leaves the tank is the product of the concentration and the rate at which water flows out: \[ \textrm{Sucrose rate out} = \underbrace{\left(\frac{y}{600+20t} \frac{\textrm{kg}}{\textrm{L}}\right) \left(20 \frac{\textrm{L}}{\textrm{min}} \right)}_{\textrm{Concentration times water rate out}} = \frac{20y}{600+20t} = \frac{y}{t+30} \text{kg/min} \] Now Eq. (7) gives us the differential equation \[ \begin{equation} \label{10.firstord.mix} \frac{dy}{dt} = 4 - \frac{y}{t + 30} \tag {8} \end{equation} \]

Step 2. Find the general solution

We write Eq. (8) in standard form: \[ \begin{equation} \label{10.firstord.std} \frac{dy}{dt} + \underbrace{\frac{1}{t+30}}_{A(t)}\,y = \underbrace{4}_{B(t)} \tag {9} \end{equation} \] An integrating factor is \[ \alpha(t) = e^{\int A(t)\,dt} = e^{\int dt/(t+30)}=e^{\ln(t+30)}=t+30 \] The general solution is \[ \begin{align*} y(t) &= \alpha(t)^{-1} \left(\int \alpha(t)B(t)\,dt + C\right) \\&= \frac{1}{t+30} \left(\int (t+30)(4)\,dt + C\right) \\ &= \frac{1}{t+30}\big(2(t+30)^2+C\big) = 2t+60 +\frac{C}{t+30} \end{align*}\]

Step 3. Solve the initial value problem

At \(t=0\), the tank contains 600 L of water with a sucrose concentration of \(0.2 \text{kg/L}\). Thus, the total sucrose at \(t = 0\) is \(y(0)=(600)(0.2)=120\) kg, and \[ y(0) = 2(0)+60 + \frac{C}{0+30} = 60 + \frac{C}{30} = 120\quad\Rightarrow\quad C=1800 \] We obtain the following formula (\(t\) in minutes), which is valid until the tank overflows: \[ y(t) = 2t+60 +\frac{1800}{t+30} \text{kg sucrose} \]