exercise
Question 11.95
Verify that interchanging the first two rows of the \(3 \times 3\) determinant \[ \Bigg|\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1 & 2 & 1 \\ 3 & 0 & 1 \\ 2 & 0 & 2 \end{array} \Bigg| \] changes the sign of the determinant.
Question 11.96
Evaluate the determinants
- (a) \(\begin{array}[t]{@{}|c@{\quad}r@{\quad}c|@{}} 2 & -1 & 0 \\ 4 &3 & 2 \\ 3 & 0 & 1 \end{array}\)
- (b) \(\begin{array}[t]{@{}|r@{\quad}r@{\quad}r|@{}} 36 & 18 & 17 \\ 45 & 24 & 20 \\ 3 & 5 & -2 \end{array}\)
- (c) \(\begin{array}[t]{@{}|c@{\quad}r@{\quad}r|@{}} 1 & 4 & 9 \\ 4 & 9 & 16 \\ 9 & 16 & 25 \end{array}\)
- (d) \(\begin{array}[t]{@{}|r@{\quad}r@{\quad}r|@{}} 2 & 3 & 5 \\ 7 & 11 & 13 \\ 17 & 19 & 23 \end{array}\)
Question 11.97
Compute \({\bf a} \times {\bf b}\), where \({\bf a} = {\bf i} - 2 {\bf j} + {\bf k} , {\bf b} = 2 {\bf i} + {\bf j} + {\bf k}.\)
Question 11.98
Compute \({\bf a} \,{\cdot}\, ( {\bf b} \times {\bf c})\), where a and b are as in Exercise 3 and \({\bf c} = 3 {\bf i} - {\bf j} + 2 {\bf k}\).
Question 11.99
Find the area of the parallelogram with sides a and b given in Exercise 3.
Question 11.100
A triangle has vertices \((0,0,0), (1,1,1)\), and \((0,-2,3)\). Find its area.
Question 11.101
What is the volume of the parallelepiped with sides \(2 {\bf i} + {\bf j} - {\bf k}, 5 {\bf i} - 3 {\bf k},\) and \({\bf i} - 2 {\bf j} + {\bf k}\)?
Question 11.102
What is the volume of the parallelepiped with sides \({\bf i}, 3 {\bf j} -{\bf k},\) and \(4 {\bf i} + 2 {\bf j} - {\bf k}\)?
In Exercises 9 to 12, describe all unit vectors orthogonal to both of the given vectors.
Question 11.103
\({\bf i,j}\)
Question 11.104
\(-5 {\bf i} + 9 {\bf j} - 4 {\bf k} , 7 {\bf i} + 8 {\bf j} + 9 {\bf k}\)
Question 11.105
\(-5 {\bf i} + 9 {\bf j} - 4 {\bf k} , 7 {\bf i} + 8 {\bf j} + 9 {\bf k}\)
Question 11.106
\(2 {\bf i} - 4 {\bf j} + 3 {\bf k} , - 4 {\bf i} + 8 {\bf j} - 6 {\bf k}\)
Question 11.107
Compute \({\bf u} + {\bf v} , {\bf u} \,{\cdot}\, {\bf v} , \| {\bf u} \|, \| {\bf v} \|,\) and \({\bf u} \times {\bf v}\), where \({\bf u} = {\bf i} - 2 {\bf j} + {\bf k} , {\bf v} = 2 {\bf i} - {\bf j} + 2 {\bf k}.\)
Question 11.108
Repeat Exercise 13 for \({\bf u} = 3 {\bf i} + {\bf j} - {\bf k} , {\bf v} = - 6 {\bf i} - 2 {\bf j} - 2 {\bf k}.\)
50
Question 11.109
Find an equation for the plane that
- (a) is perpendicular to \({\bf v} = (1,1,1)\) and passes through \((1, 0, 0).\)
- (b) is perpendicular to \({\bf v}= (1, 2, 3)\) and passes through \((1, 1, 1).\)
- (c) is perpendicular to the line \({\bf l} (t) = (5,0,2) t + (3,-1,1)\) and passes through \((5, -1, 0).\)
- (d) is perpendicular to the line \({\bf l} (t) = (-1, -2,3) t + ( 0,7,1)\) and passes through \((2,4,-1).\)
Question 11.110
Find an equation for the plane that passes through
- (a) \((0, 0, 0), (2, 0, -1)\), and \((0, 4, -3)\).
- (b) \((1, 2, 0), (0, 1, -2)\), and \((4, 0, 1)\).
- (c) \((2, -1, 3),(0, 0, 5),\) and \((5, 7, -1)\).
Question 11.111
Show that the points \((0, -2, -1), (1, 4, 0), (2, 10, 1)\) do not determine a unique plane.
Question 11.112
Let \(P\) be the plane defined by the equation \(x+y+z=1\). Which of the following points are contained in \(P\)?
- (a) (0, 0, 0)
- (b) (1, 1, \(-1\))
- (c) (\(-3\), 8, \(-4\))
- (d) (1, 2, \(-3\))
Question 11.113
- (a) Show that two parallel planes are either identical or they never intersect.
- (b) How do two nonparallel planes intersect?
Question 11.114
Find the intersection of the planes \(x + 2y+z = 0\) and \(x- 3y - z = 0\).
Question 11.115
Find the intersection of the planes \(x + (\kern1pty - 1) + z = 0\) and \({-}x + (\kern1pty + 1) - z = 0\).
Question 11.116
Find the intersection of the two planes with equations \(3(x- 1) + 2y + (z + 1) = 0\) and \((x- 1) + 4y- (z + 1) = 0\).
Question 11.117
- (a) Prove the two triple-vector-product identities \[ ({\bf a}\, \times\, {\bf b} )\, \times\, {\bf c} = ( {\bf a}\,{\cdot}\,{\bf c}) {\bf b}\, - ( {\bf b}\,{\cdot}\,{\bf c}){\bf a} \] and \[ {\bf a}\, \times \,( {\bf b}\, \times\, {\bf c}) = ( {\bf a}\,{\cdot}\,{\bf c}) {\bf b} - ( {\bf a}\,{\cdot}\,{\bf b} ) {\bf c}. \]
- (b) Prove \(({\bf u} \,\times\, {\bf v}) \,\times\, {\bf w} = {\bf u} \,\times\, ( {\bf v} \,\times\, {\bf w})\) if and only if \(({\bf u} \,\times\, {\bf w}) \,\times\, {\bf v} ={\bf 0}\).
- (c) Also prove that \(( {\bf u} \times {\bf v}) \times {\bf w} + ( {\bf v} \times {\bf w}) \times {\bf u} + ( {\bf w} \times {\bf u} ) \times {\bf v} ={\bf 0}\) (called the Jacobi identity).
Question 11.118
- (a) Prove, without recourse to geometry, that \begin{eqnarray*} {\bf u} \,{\cdot}\, ( {\bf v} \times {\bf w} ) &=& {\bf v} \,{\cdot}\, ( {\bf w} \times {\bf u} ) = {\bf w} \,{\cdot}\, ( {\bf u} \times {\bf v} ) = - {\bf u} \,{\cdot}\, ( {\bf w} \times {\bf v}) \\ & = & - {\bf w} \,{\cdot}\, ( {\bf v} \times {\bf u}) =- {\bf v} \,{\cdot}\, ( {\bf u} \times {\bf w} ).\\[-19.5pt] \end{eqnarray*}
- (b) Use part (a) and Exercise 23(a) to prove that \begin{eqnarray*} ( {\bf u} \times {\bf v})\,{\cdot}\, ({\bf u}' \times {\bf v}' ) &=& ( {\bf u} \,{\cdot}\, {\bf u}') ( {\bf v} \,{\cdot}\, {\bf v}') - ( {\bf u} \,{\cdot}\, {\bf v}') ( {\bf u}' \,{\cdot}\, {\bf v})\\[3pt] &=& \Big|\begin{array}{@{}l@{\quad}c@{}} {\bf u} \ {\cdot} \ {\bf u}' & {\bf u} \,{\cdot}\, {\bf v}' \\ {\bf u}' \,{\cdot}\,\, {\bf v} & {\bf v} \,{\cdot}\, {\bf v}' \end{array}\Big|. \end{eqnarray*}
Question 11.119
Verify Cramer’s rule.
Question 11.120
What is the geometric relation between the vectors \(\textbf{v}\) and \(\textbf{w}\) if \(\|\textbf{v} \times \textbf{w} \| = \frac{1}{2}\|\textbf{v}\| \ \|\textbf{w}\|\)?
Question 11.121
Let \(\textbf{v}=(1, 1, 0)\) and \(\textbf{w}=(0, 2, -1)\). Use the algebraic rules and multiplication table on page 37 to compute \(\textbf{v} \times \textbf{w}\) without using determinants.
Question 11.122
Find an equation for the plane that passes through the point \((2, -1,3)\) and is perpendicular to the line \({\bf v} = (1,-2,2) + t (3,-2,4)\).
Question 11.123
Find an equation for the plane that passes through the point \((1,2,-3)\) and is perpendicular to the line \({\bf v} = (0,-2,1) + t ( 1, -2,3)\).
Question 11.124
Find the equation of the line that passes through the point \((1,-2,-3)\) and is perpendicular to the plane \(3x - y - 2z +4 =0\).
Question 11.125
Find an equation for the plane containing the two (parallel) lines \[ {\bf v}_1 = (0,1,-2) + t ( 2,3,-1) \] and \[ {\bf v}_2 = (2,-1,0) + t (2,3,-1). \]
Question 11.126
Find a parametrization for the line perpendicular to \((2, -1, 1)\), parallel to the plane \(2x+y-4z=1\), and passing through the point \((1, 0, -3)\)
Question 11.127
Find an equation for the plane containing the point \((1, 0, 1)\) and the line \( {\bf l}(t)=(1, 2, -1) +t(1, 0, 5)\).
51
Question 11.128
Find the distance from the point \((2,1,-1)\) to the plane \(x-2y + 2z +5 =0\).
Question 11.129
Find an equation for the plane that contains the line \({\bf v} = (-1,1,2) + t (3,2,4)\) and is perpendicular to the plane \(2x + y -3z + 4=0\).
Question 11.130
Find an equation for the plane that passes through \((3,2,-1)\) and \((1,-1,2)\) and that is parallel to the line \({\bf v} = (1,-1,0) + t (3,2,-2).\)
Question 11.131
Redo Exercises 25 and 26 of Section 11.1 using the dot product and what you know about normals to planes.
Question 11.132
Given vectors a and b, do the equations \({\bf x} \times {\bf a} = {\bf b}\) and \({\bf x} \,\,{\cdot}\,\, {\bf a} = \|{\bf a}\|\) determine a unique vector x? Argue both geometrically and analytically.
Question 11.133
Determine the distance from the plane \(12x + 13y + 5z + 2 =0\) to the point \((1,1,-5)\).
Question 11.134
Find the distance to the point (6, 1, 0) from the plane through the origin that is perpendicular to \({\bf i}- 2 {\bf j} + {\bf k}.\)
Question 11.135
- (a) In mechanics, the moment Mof a force about a point O is defined to be the magnitude of F times the perpendicular distance \(d\) from O to the line of action of F. The vector moment M is the vector of magnitude M whose direction is perpendicular to the plane of O and F, determined by the right-hand rule. Show that \({\bf M} = {\bf R} \times {\bf F}\), where \({\bf R}\) is any vector from O to the line of action of F. (See Figure 11.59.)
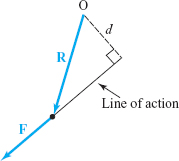 Figure 11.59: Moment of a force.
Figure 11.59: Moment of a force. - (b) Find the moment of the force vector \({\bf F}={\bf i}\,-\,{\bf j}\,+\,2{\bf k}\) newtons about the origin if the line of action is \(x=1+t\), \(y=1-t\), \(z=2t\).
Question 11.136
Show that the plane that passes through the three points \(A=(a_1,a_2,a_3), B= (b_1,b_2,b_3)\), and \(C=(c_1,c_2,c_3)\) consists of the points \({\rm P}=(x,y,z)\) given by \[ \Bigg|\begin{array}{@{}c@{\quad}c@{\quad}r @{}} a_1-x&a_2-y&a_3-z\\ b_1-x&b_2-y&b_3-z\\ c_1-x&c_2-y&c_3-z \end{array}\Bigg|=0. \]
( HINT: Write the determinant as a triple product.)
Question 11.137
Two media with indices of refraction \(n_1\) and \(n_2\) are separated by a plane surface perpendicular to the unit vector N. Let a and b be unit vectors along the incident and refracted rays, respectively, their directions being those of the light rays. Show that \(n_1 ( {\bf N} \times {\bf a}) = n_2 ( {\bf N} \times {\bf b})\) by using Snell’s law, \(\sin \theta_1 /\sin \theta_2 = n_2 / n_1\), where \(\theta_1\) and \(\theta_2\) are the angles of incidence and refraction, respectively. (See Figure 11.60.)

Question 11.138
Justify the steps in the following computation: \begin{eqnarray*} \Bigg|\begin{array} &1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 10 \end{array} \Bigg| &=& \Bigg|\begin{array} &1 & 2 & 3 \\ 0 & -3 & -6 \\ 7 & 8 & 10 \end{array} \Bigg| \,=\,\Bigg|\begin{array} &1 & 2 & 3 \\ 0 & -3 & -6 \\ 0 & -6 & -11 \end{array} \Bigg|\\ &=&\Big|\begin{array} &-3 & -6 \\ -6 & -11 \end{array}\Big| = 33-36=-3 . \end{eqnarray*}
Question 11.139
Show that adding a multiple of the first row of a matrix to the second row leaves the determinant unchanged; that is, \[ \Bigg|\begin{array} &a_1 & b_1 & c_1 \\ a_2+ \lambda a_1 & b_2 + \lambda b_1 & c_2 + \lambda c_1 \\ a_3 & b_3 & c_3 \end{array} \Bigg| = \Bigg|\begin{array} &a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{array} \Bigg|. \] [In fact, adding a multiple of any row (column) of a matrix to another row (column) leaves the determinant unchanged.]
Question 11.140
Suppose \(\textbf{v}, \ \textbf{w} \in \mathbb{R}^3\) are orthogonal unit vectors. Let \(\textbf{u} = \textbf{v} \times \textbf{w}\). Show that \(\textbf{w} = \textbf{u} \times \textbf{v}\) and \(\textbf{v} = \textbf{w} \times \textbf{u}\).