1.6 A Survey of Quadric Surfaces

New section content

Quadric surfaces are the surface analogs of conic sections. Recall that a conic section is a curve in \(\textbf{R}^2\) defined by a quadratic equation in two variables. A quadric surface is defined by a quadratic equation in three variables: \begin{equation} Ax^2+By^2+Cz^2+Dxy+Eyz+Fzx+ax+by+cz+d=0\tag{1} \end{equation}

Like conic sections, quadric surfaces are classified into a small number of types. When the coordinate axes are chosen to coincide with the axes of the quadric, the equation of the quadric has a simple form. The quadric is then said to be in standard position. In standard position, the coefficients \(D\), \(E\), \(F\) are all zero and the linear part \((ax+by+cz+d)\) also reduces to just one term. In this short survey of quadric surfaces, we restrict our attention to quadrics in standard position.

Note

To ensure that Eq.(1) is genuinely quadratic, we assume that the degree-2 coefficients \(A, B, C, D, E, F\) are not all zero.

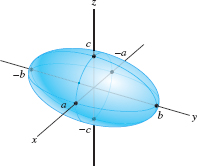
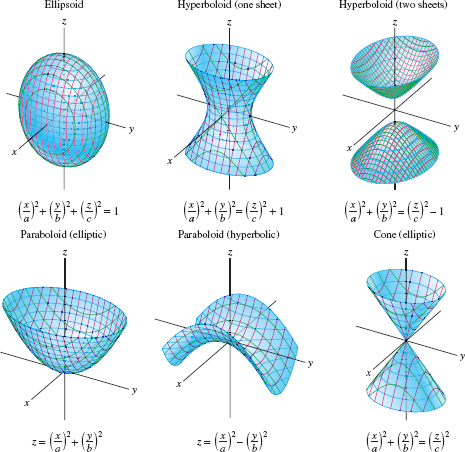
The surface analogs of ellipses are the egg-shaped ellipsoids (Figure 1.87). In standard form, an ellipsoid has the equation \[ \boxed{\textbf{Ellipsoid}\qquad \left(\frac{x}a\right)^2+\left(\frac{y}b\right)^2+\left(\frac{z}c\right)^2=1 }\]

For \(a=b=c\), this equation is equivalent to \(x^2+y^2+z^2=a^2\) and the ellipsoid is a sphere of radius \(a\).

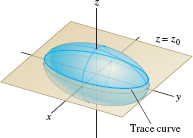
Surfaces are often represented graphically by a mesh of curves called traces, obtained by intersecting the surface with planes parallel to one of the coordinate planes (Figure 1.88). Algebraically, this corresponds to freezing one of the three variables (holding it constant). For example, the intersection of the horizontal plane \(z=z_0\) with the surface is a horizontal trace curve.

image
Figure 1.87: Ellipsoid with equation \({\left(\frac{x}a\right)^2+\left(\frac{y}b\right)^2+\left(\frac{z}c\right)^2=1}\).

706

EXAMPLE 1 The Traces of an Ellipsoid

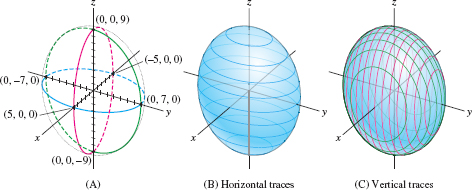
Describe the traces of the ellipsoid \[ \left(\frac{x}5\right)^2 + \left(\frac{y}7\right)^2 + \left(\frac{z}9\right)^2 = 1 \]

Solution First we observe that the traces in the coordinate planes are ellipses (Figure 1.89): \begin{align*} &\textrm{\(xy\)-trace (set \(z=0\), blue in figure):}&\qquad &\left(\frac{x}5\right)^2 + \left(\frac{y}7\right)^2 = 1\\ &\textrm{\(yz\)-trace (set \(x=0\), green in figure):}&\qquad & \left(\frac{y}7\right)^2 + \left(\frac{z}9\right)^2 = 1\\ &\textrm{\(xz\)-trace (set \(y=0\), red in figure):}&\qquad &\left(\frac{x}5\right)^2 + \left(\frac{z}9\right)^2 = 1 \end{align*}

In fact, all the traces of an ellipsoid are ellipses. For example, the horizontal trace defined by setting \(z=z_0\) is the ellipse [Figure 1.89] \[ \textrm{Trace at height \(z_0\):}\quad \left(\frac{x}5\right)^2 + \left(\frac{y}7\right)^2 + \left(\frac{z_0}9\right)^2 = 1\qquad \textrm{or}\qquad \frac{x^2}{25} + \frac{y^2}{49} = \underbrace{1 - \frac{z_0^2}{81}}_{\textrm{A constant}} \]

The trace at height \(z_0=9\) is the single point \((0,0,9)\) because \({{x^2}/{25} + {y^2}/{49}=0}\) has only one solution: \(x=0, y=0\). Similarly, for \(z_0 = -9\) the trace is the point \((0,0,-9)\). If \(|z_0| \gt 9\), then \(1-z_0^2/81 \lt 0\) and the plane lies above or below the ellipsoid. The trace has no points in this case. The traces in the vertical planes \(x=x_0\) and \(y=y_0\) have a similar description [Figure 1.89].

image
Figure 1.88: The intersection of the plane \(z= z_0\) with an ellipsoid is an ellipse.
image
Figure 1.89: The ellipsoid \(\left(\dfrac{x}{5}\right)^2 + \left(\dfrac{y}{7}\right)^2 + \left(\dfrac{z}{9}\right)^2 = 1\).

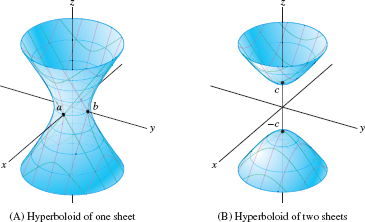
The analogs of the hyperbolas are the hyperboloids, which come in two types, depending on whether the surface has one or two components. We refer to these types as hyperboloids of one or two sheets (Figure 1.90). Their equations in standard position are \begin{equation} \textbf{Hyperboloids} \qquad\textrm{One Sheet:} \displaystyle{\left(\frac{x}a\right)^2 + \left(\frac{y}b\right)^2 = \left(\frac{z}c\right)^2 + 1} \\[8pt] \qquad \qquad \qquad \qquad \textrm{Two Sheets:} \displaystyle{\left(\frac{x}a\right)^2 + \left(\frac{y}b\right)^2 = \left(\frac{z}c\right)^2 -1} \tag{2} \end{equation}

707

Notice that a hyperboloid of two sheets does not contain any points whose \(z\)-coordinate satisfies \(-c \lt z \lt c\) because the right-hand side \({\left(\frac{z}c\right)^2 -1}\) is then negative, but the left-hand side of the equation is greater than or equal to zero.

image
Figure 1.90: Hyperboloids of one and two sheets.

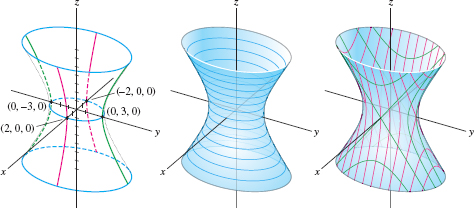
EXAMPLE 2 The Traces of a Hyperboloid of One Sheet

Determine the traces of the hyperboloid \({ \left(\frac{x}2\right)^2 + \left(\frac{y}3\right)^2 = \left(\frac{z}4\right)^2 + 1}\).

Solution The horizontal traces are ellipses and the vertical traces (parallel to both the \(yz\)-plane and the \(xz\)-plane) are hyperbolas (Figure 1.91): \begin{align*} &\textrm{Trace \(z=z_0\) (ellipse, blue in figure):}&\qquad&\left(\frac{x}2\right)^2 + \left(\frac{y}3\right)^2 = \left(\frac{z_0}4\right)^2 + 1\\ &\textrm{Trace \(x=x_0\) (hyperbola, green in figure):}&\qquad & \left(\frac{y}3\right)^2 - \left(\frac{z}4\right)^2 = 1-\left(\frac{x_0}2\right)^2\\ &\textrm{Trace \(y=y_0\) (hyperbola, red in figure):}&\qquad&\left(\frac{x}2\right)^2 - \left(\frac{z}4\right)^2 = 1 - \left(\frac{y_0}3\right)^2 \end{align*}

image
Figure 1.91: The hyperboloid \(\left(\dfrac{x}{2}\right)^2+\left(\dfrac{y}{3}\right)^2 =\left(\dfrac{z}{4}\right)^2 + 1\).

708

EXAMPLE 3 Hyperboloid of Two Sheets Symmetric about the \(y\)-axis

Show that \({ \left(\frac{x}a\right)^2 + \left(\frac{z}c\right)^2 = \left(\frac{y}b\right)^2 - 1}\) has no points for \(-b \lt y \lt b\).

Solution This equation does not have the same form as Eq.(3) because the variables \(y\) and \(z\) have been interchanged. This hyperboloid is symmetric about the \(y\)-axis rather than the \(z\)-axis (Figure 1.92). The left-hand side of the equation is always \(\geq 0\). Thus, there are no solutions with \(|y| \lt b\) because the right-hand side is \({\left(\tfrac{y}b\right)^2-1 \lt 0}\). Therefore, the hyperboloid has two sheets, corresponding to \(y\ge b\) and \(y\le -b\).

image
Figure 1.92: The two-sheeted hyperboloid \(\left(\dfrac{x}{a}\right)^2 + \left(\dfrac{z}{c}\right)^2 = \left(\dfrac{y}{b}\right)^2 - 1\).
image
Figure 1.93: Elliptic cone \({\left(\frac{x}{a}\right)^2 + \left(\frac{y}{b}\right)^2 = \left(\frac{z}{c}\right)^2}\).

The following equation defines an elliptic cone (Figure 1.93): \[\boxed{ \textbf{Elliptic Cone:}\qquad\left(\frac{x}a\right)^2+\left(\frac{y}b\right)^2= \left(\frac{z}c\right)^2 }\]

An elliptic cone may be thought of as a limiting case of a hyperboloid of one sheet in which we “pinch the waist” down to a point.

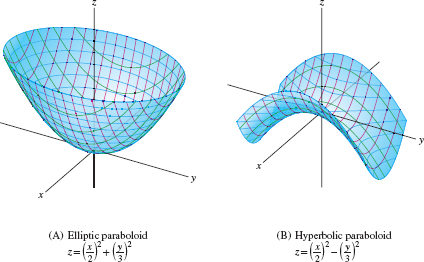
The third main family of quadric surfaces are the paraboloids. There are two types—elliptic and hyperbolic. In standard position, their equations are \begin{equation} \textbf{Paraboloids} \qquad\textrm{Elliptic:} \displaystyle{z = \Big(\frac{x}a\Big)^2+\Big(\frac{y}b\Big)^2} \\[8pt] \qquad\qquad\qquad\textrm{Hyperbolic:} \displaystyle{z = \Big(\frac{x}a\Big)^2 - \Big(\frac{y}b\Big)^2} \tag{3} \end{equation}

Let's compare their traces (Figure 1.94):

Elliptic paraboloid Hyperbolic paraboloid
Horizontal traces ellipses hyperbolas
Vertical traces upward parabolas upward and downward parabolas
image

709

Notice, for example, that for the hyperbolic paraboloid, the vertical traces \(x=x_0\) are downward parabolas (green in the figure) \[ \underbrace{z = -\left(\frac{y}b\right)^2 + \left(\frac{x_0}a\right)^2}_{\textrm{Trace \(x=x_0\) of hyperbolic paraboloid}} \]

whereas the vertical traces \(y=y_0\) are upward parabolas (red in the figure) \[ \underbrace{z = \left(\frac{x}a\right)^2 - \left(\frac{y_0}b\right)^2}_{\textrm{Trace \(y=y_0\) of hyperbolic paraboloid}} \]

EXAMPLE 4 Alternative Form of a Hyperbolic Paraboloid

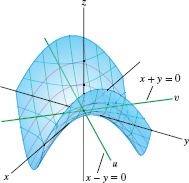
Show that \(z=4xy\) is a hyperbolic paraboloid by writing the equation in terms of the variables \(u=x+y\) and \(\textbf{v}=x-y\).

Solution Note that \(u+v=2x\) and \(u-v= 2y\). Therefore, \[ 4xy = (u+v)(u-v) = u^2-v^2 \]

and thus the equation takes the form \(z=u^2-v^2\) in the coordinates \(\{u,v,z\}\). The coordinates \(\{u,v,z\}\) are obtained by rotating the coordinates \(\{x,y,z\}\) by \(45^\circ\) about the \(z\)-axis (Figure 1.95).

Note

Paraboloids play an important role in the optimization of functions of two variables. The elliptic paraboloid in Figure 1.94 has a local minimum at the origin. The hyperbolic paraboloid is a “saddle shape” at the origin, which is an analog for surfaces of a point of inflection.

image
Figure 1.95: The hyperbolic paraboloid is defined by \(z=4xy\) or \(z=u^2-v^2\).
image
Figure 1.96: The cylinder with base \(C\).

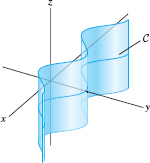
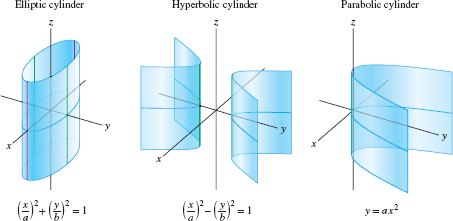
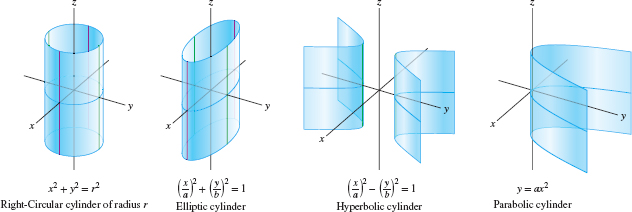
Further examples of quadric surfaces are the quadratic cylinders. We use the term cylinder in the following sense: Given a curve \(C\) in the \(xy\)-plane, the cylinder with base \(C\) is the surface consisting of all vertical lines passing through \(C\) (Figure 1.96). Equations of cylinders involve just the two variables \(x\) and \(y\). The equation \(x^2 + y^2 = r^2\) defines a circular cylinder of radius \(r\) with the \(z\)-axis as central axis. Figure 1.97 shows a circular cylinder and three other types of quadratic cylinders.

The ellipsoids, hyperboloids, paraboloids, and quadratic cylinders are called nondegenerate quadric surfaces. There are also a certain number of “degenerate” quadric surfaces. For example, \(x^2 + y^2 + z^2 = 0\) is a quadric that reduces to a single point \((0,0,0)\), and \((x + y + z)^2 = 1\) reduces to the union of the two planes \(x + y + z = \pm 1\).

710

image

Summary