1.2 The Inner Product, Length, and Distance
In this section and the next we shall discuss two products of vectors: the inner product and the cross product. These are very useful in physical applications and have interesting geometric interpretations. The first product we shall consider is called the inner product. The name dot product is often used instead.
The Inner Product
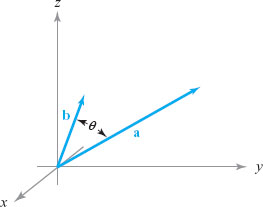
Suppose we have two vectors \({\bf a}\) and \({\bf b}\) in \({\mathbb R}^3\) (Figure 1.29) and we wish to determine the angle between them, that is, the smaller angle subtended by \({\bf a}\) and \({\bf b}\) in the plane that they span. The inner product enables us to do this. Let us first develop the concept formally and then prove that this product does what we claim. Let \({\bf a}=a_1{\bf i}+a_2{\bf j}+a_3{\bf k}\) and \({\bf b}=b_1{\bf i}+b_2{\bf j}+b_3{\bf k}\). We define the inner product of \({\bf a}\) and \({\bf b}\), written \({\bf a} \,{ \cdot}\, {\bf b},\) to be the real number \[ {\bf a} \,{ \cdot}\,{\bf b}=a_1b_1+a_2b_2+a_3b_3. \]
20
Note that the inner product of two vectors is a scalar quantity. Sometimes the inner product is denoted \(\langle {\bf a}, {\bf b}\rangle\); thus, \(\langle {\bf a}, {\bf b}\rangle\) and \({\bf a}\,{ \cdot}\, {\bf b}\) mean exactly the same thing.
example 1
- (a) If \({\bf a}=3{\bf i}+{\bf j}-2{\bf k}\) and \({\bf b}={\bf i}-{\bf j}+{\bf k}\), calculate \({\bf a}\,{ \cdot}\,{\bf b}\).
- (b) Calculate \((2{\bf i}+{\bf j}-{\bf k})\,{ \cdot}\,(3{\bf k}-2{\bf j})\).
solution
- (a) \({\bf a}\,{ \cdot}\,{\bf b}=3\,{ \cdot}\,1+1\,{ \cdot}\,(-1)+(-2)\,{ \cdot}\, 1=3-1-2=0\).
- (b) \((2{\bf i}+{\bf j}-{\bf k})\,{ \cdot}\,(3{\bf k}-2{\bf j})=(2{\bf i}+{\bf j}-{\bf k})\,{ \cdot}\, (0{\bf i}-2{\bf j}+3{\bf k})\hphantom{(2{\bf i}+{\bf j}-{\bf k})\,{ \cdot}\,(3{\bf k}-2{\bf j})} \\ \qquad\qquad\qquad\qquad\qquad =2\,{ \cdot}\, 0-1\,{ \cdot}\, 2-1\,{ \cdot}\, 3=-5.\)
Certain properties of the inner product follow from the definition. If \({\bf a,b}\), and \({\bf c}\) are vectors in \({\mathbb R}^3\) and \(\alpha\) and \(\beta\) are real numbers, then
- (i) \({\bf a}\,{ \cdot}\,{\bf a}\ge 0;\)
\({\bf a}\,{ \cdot}\,{\bf a}=0 \qquad \hbox{ if and only if} \qquad {\bf a}={\bf 0}\).
- (ii) \(\alpha {\bf a}\,{ \cdot}\,{\bf b}=\alpha({\bf a}\,{ \cdot}\,{\bf b})\qquad {\rm and} \qquad {\bf a} \,{ \cdot}\, \beta {\bf b}=\beta({\bf a}\,{ \cdot}\,{\bf b}).\)
- (iii) \({\bf a}\,{ \cdot}\,({\bf b}+{\bf c})={\bf a}\,{ \cdot}\,{\bf b}+ {\bf a}\,{ \cdot}\,{\bf c}\qquad {\rm and} \qquad ({\bf a}+{\bf b})\,{ \cdot}\, {\bf c}={\bf a} \,{ \cdot}\,{\bf c}+ {\bf b}\,{ \cdot}\,{\bf c}.\)
- (iv) \({\bf a}\,{ \cdot}\,{\bf b}={\bf b}\,{ \cdot}\,{\bf a}.\)
To prove the first of these properties, observe that if \({\bf a}=a_1{\bf i}+a_2{\bf j}+a_3{\bf k}\), then \({\bf a}\,{ \cdot}\,{\bf a}=a_1^2+a_2^2+a_3^2\). Because \(a_1,a_2\), and \(a_3\) are real numbers, we know \(a_1^2\ge 0, a_2^2\ge 0, a^2_3 \ge 0\). Thus, \({\bf a}\,{ \cdot}\,{\bf a}\ge 0\). Moreover, if \(a_1^2+a_2^2+a_3^2=0\), then \(a_1=a_2= a_3=0\); therefore, \({\bf a=0}\) (zero vector). The proofs of the other properties of the inner product are also easily obtained.
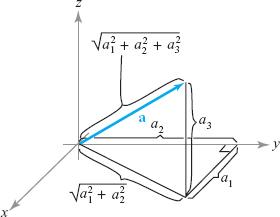
It follows from the Pythagorean theorem that the length of the vector \({\bf a}=a_1{\bf i}\) \(+\) \(a_2{\bf j}+\) \(a_3{\bf k}\) is \(\sqrt{a_1^2+a_2^2+a_3^2}\) (see Figure 1.30). The length of the vector \({\bf a}\) is denoted by \(\|{\bf a}\|\). This quantity is often called the norm of a. Because \({\bf a}\,{ \cdot}\,{\bf a}=a_1^2+a_2^2+a_3^2\), it follows that \[ \|{\bf a}\|=({\bf a}\,{ \cdot}\,{\bf a})^{1/2}. \]
Unit Vectors
21
Vectors with norm 1 are called unit vectors. For example, the vectors \({\bf i,j,k}\) are unit vectors. Observe that for any nonzero vector \({\bf a,a}/\|{\bf a}\|\) is a unit vector; when we divide a by \(\|{\bf a}\|\), we say that we have normalized \({\bf a}\).
example 2
- (a) Normalize \({\bf v}=2{\bf i}+3{\bf j}-\frac{1}{2}{\bf k}\).
- (b) Find unit vectors \({\bf a},{\bf b}\), and \({\bf c}\) in the plane such that \({\bf b}+{\bf c}={\bf a}\).
solution
- (a) We have \(\|{\bf v}\|={\textstyle\sqrt{2^2+3^2+(1/2)^2}}=(1/2)\sqrt{53}\), so the normalization of \({\bf v}\) is \[ {\bf u}=\frac{1}{\|{\bf v}\|}\, {\bf v}=\frac{4}{\sqrt{53}}\, {\bf i}+ \frac{6}{\sqrt{53}}\, {\bf j}-\frac{1}{\sqrt{53}}\, {\bf k}. \]
- (b) Because all three vectors are to have length 1, a triangle with sides \({\bf a},{\bf b}\), and \({\bf c}\) must be equilateral, as in Figure 1.31. If we orient the triangle as in the figure and we take \({\bf a}={\bf i}\), then necessarily \[ {\bf b}=\frac{1}{2}{\bf i}+ \frac{\sqrt{3}}{2}{\bf j},\qquad \hbox{and}\qquad {\bf c}=\frac{1}{2}{\bf i}-\frac{\sqrt{3}}{2} {\bf j}. \] Note that indeed \(\|{\bf a}\|=\|{\bf b}\|=\|{\bf c}\|=1\) and that \({\bf b}+{\bf c}={\bf a}\).
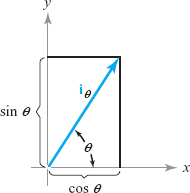
In the plane, define the vector \({\bf i}_\theta =(\cos \theta){\bf i} \,{+}\,(\sin \theta){\bf j}\), which is the unit vector making an angle \(\theta\) with the \(x\) axis (see Figure 1.32).
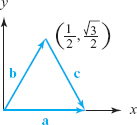
Distance
If \({\bf a}\) and \({\bf b}\) are vectors, we have seen that the vector \({\bf b}-{\bf a}\) is parallel to and has the same magnitude as the directed line segment from the endpoint of \({\bf a}\) to the endpoint of \({\bf b}\). It follows that the distance from the endpoint of \({\bf a}\) to the endpoint of \({\bf b}\) is \(\|{\bf b} - {\bf a}\|\) (see Figure 1.33).
Inner Product, Length, and Distance
Letting \({\bf a}=a_1{\bf i}+a_2{\bf j}+a_3{\bf k}\) and \({\bf b}=b_1{\bf i}+b_2{\bf j}+b_3{\bf k}\), their inner product is \[ {\bf a}\,{ \cdot}\,{\bf b} = a_1b_1+a_2b_2+a_3b_3, \] while the length of a is \[ \|{\bf a}\| = \sqrt{{\bf a}\, { \cdot}\,{\bf a}} = \sqrt{a_1^2+a_2^2+a_3^2}. \]
To normalize a vector \({\bf a}\), form the vector \[ \frac{{\bf a}}{\|{\bf a}\|}. \]
The distance between the endpoints of \({\bf a}\) and \({\bf b}\) is \(\|{\bf a}-{\bf b}\|\), and the distance between P and Q is \(\|\overrightarrow{\rm PQ\vphantom{^\prime}}\|\).
22
example 3
Find the distance from the endpoint of the vector \({\bf i}\), that is, the point \((1, 0, 0)\), to the endpoint of the vector \({\bf j}\), that is, the point \((0,1,0).\)
solution
\(\|{\bf j}-{\bf i}\|=\sqrt{(0-1)^2+(1-0)^2+(0-0)^2}=\sqrt{2}.\)
The Angle Between Two Vectors
Let us now show that the inner product does indeed measure the angle between two vectors.
Theorem 1
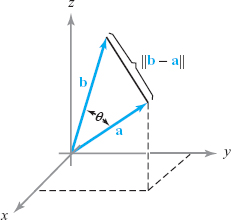
Let \({\bf a}\) and \({\bf b}\) be two vectors in \({\mathbb R}^3\) {and let} \(\theta\), {where} \(0\le \theta\le \pi ,\) be the angle between them (Figure 1.34). Then \[ {\bf a}\,{ \cdot}\,{\bf b}=\|{\bf a}\| \|{\bf b}\| \cos \theta. \]
It follows from the equation \({\bf a}\, { \cdot}\, {\bf b} =\|{\bf a}\|\|{\bf b}\| \cos\theta \) that if \({\bf a}\) and \({\bf b}\) are nonzero, we may express the angle between them as \[ \theta=\cos^{-1}\kern-2pt\left(\frac{{\bf a}\,{ \cdot}\,{\bf b}}{\|{\bf a}\| \|{\bf b}\|}\right)\kern-2pt. \]
proof
If we apply the law of cosines from trigonometry to the triangle with one vertex at the origin and adjacent sides determined by the vectors \({\bf a}\) and \({\bf b}\) (as in the figure), it follows that \[ \|{\bf b-a}\|^2=\|{\bf a}\|^2+\|{\bf b}\|^2-2\|{\bf a}\|\|{\bf b}\|\cos \theta. \]
Because \(\|{\bf b}-{\bf a}\|^2=({\bf b}-{\bf a})\,{ \cdot}\, ({\bf b}-{\bf a}),\|{\bf a}\|^2= {\bf a}\,{ \cdot}\,{\bf a}\), and \(\|{\bf b}\|^2={\bf b}\,{ \cdot}\,{\bf b}\), we can rewrite the preceding equation as \[ ({\bf b}-{\bf a})\,{ \cdot}\, ({\bf b}-{\bf a})={\bf a}\,{ \cdot}\,{\bf a}+ {\bf b}\,{ \cdot}\,{\bf b}-2\|{\bf a}\| \|{\bf b}\| \cos \theta. \]
23
We can also expand \(({\bf b}-{\bf a})\, { \cdot}\, ({\bf b}-{\bf a})\) as follows: \begin{eqnarray*} ({\bf b}-{\bf a}) \,{ \cdot}\,( {\bf b}-{\bf a}) &=&{\bf b}\,{ \cdot}\, ({\bf b}-{\bf a})-{\bf a}\,{ \cdot}\, ({\bf b}-{\bf a})\\ &=&{\bf b}\,{ \cdot}\,{\bf b}-{\bf b}\,{ \cdot}\,{\bf a}- {\bf a}\,{ \cdot}\,{\bf b}+{\bf a}\,{ \cdot}\,{\bf a}\\ &=&{\bf a}\,{ \cdot}\,{\bf a}+{\bf b}\,{ \cdot}\,{\bf b}-2 {\bf a}\,{ \cdot}\,{\bf b}. \end{eqnarray*} Thus, \[ {\bf a}\,{ \cdot}\,{\bf a}+{\bf b}\,{ \cdot}\,{\bf b}-2{\bf a}\,{ \cdot}\,{\bf b} ={\bf a}\,{ \cdot}\,{\bf a}+{\bf b}\,{ \cdot}\,{\bf b} -2\|{\bf a}\| \|{\bf b}\|\cos \theta. \] That is, \[ {\bf a} \,{ \cdot}\,{\bf b}=\|{\bf a}\| \|{\bf b}\|\cos \theta. \]
example 4
Find the angle between the vectors \({\bf i}+{\bf j}+{\bf k}\) and \({\bf i}+{\bf j}-{\bf k}\) (see Figure 1.4).
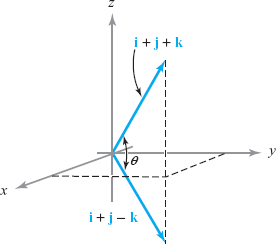
solution Using Theorem \(1,\) we have \[ ({\bf i}+{\bf j}+{\bf k}) \,{ \cdot}\, ( {\bf i}+{\bf j}-{\bf k})= \|{\bf i}+{\bf j}+{\bf k}\| \|{\bf i}+{\bf j}-{\bf k}\|\cos \theta, \] and so \[ 1+1-1=(\sqrt{3})(\sqrt{3})\cos \theta. \] Hence, \[ \cos \theta={\textstyle \frac{1}{3}}. \] That is, \[ \theta=\cos^{-1} ({\textstyle \frac{1}{3}})\approx 1.23 \hbox{ radians } (71^\circ). \]
The Cauchy–Schwarz Inequality
Theorem 1 shows that the inner product of two vectors is the product of their lengths times the cosine of the angle between them. This relationship is often of value in problems of a geometric nature. An important consequence of Theorem 1 is:
24
Corollary Cauchy–Schwarz Inequality
For any two vectors a and b\({,}\) we have \[ |{\bf a}\,{ \cdot}\,{\bf b}|\le \|{\bf a}\| \|{\bf b}\| \] with equality if and only if \({\bf a}\) is a scalar multiple of \({\bf b},\) or one of them is \({\bf 0}\).
proof
If a is not a scalar multiple of \({\bf b}\), then \(\theta\), the angle between them, is not zero or \(\pi\), and so \(|{\cos \theta} | < 1\), and thus the inequality holds; in fact, if a and b are both nonzero, strict inequality holds in this case. When \({\bf a}\) is a scalar multiple of \({\bf b}\), then \(\theta=0\) or \(\pi\) and \(|{\cos \theta}|=1\), so equality holds in this case.
example 5
Verify the Cauchy–Schwarz inequality for \({\bf a}=-{\bf i}+{\bf j}+{\bf k}\) and \({\bf b}=\) \(3{\bf i}+{\bf k}\).
solution The dot product is \({\bf a}\,{ \cdot}\,{\bf b}=-3+0+1=-2\), so \(|{\bf a}\,{ \cdot}\,{\bf b}|=2\). Also, \(\|{\bf a}\|=\sqrt{1+1+1}=\sqrt{3}\) and \(\|{\bf b}\|=\sqrt{9+1}=\sqrt{10}\), and it is true that \(2\leq \sqrt{3}\,{ \cdot}\,\sqrt{10}\) because \(\sqrt{3}\,{ \cdot}\,\sqrt{10}> \sqrt{3}\,{ \cdot}\,\sqrt{3}=3\geq 2\).
If \({\bf a}\) and \({\bf b}\) are nonzero vectors in \({\mathbb R}^3\) and \(\theta\) is the angle between them, we see that \({\bf a}\,{ \cdot}\,{\bf b} = 0\) if and only if \(\cos \theta=0\). Thus, the inner product of two nonzero vectors is zero if and only if the vectors are perpendicular. Hence, the inner product provides us with a convenient method for determining whether two vectors are perpendicular. Often we say that perpendicular vectors are orthogonal. The standard basis vectors \({\bf i,j}\), and \({\bf k}\) are mutually orthogonal and of length 1; any such system is called orthonormal. We shall adopt the convention that the zero vector is orthogonal to all vectors.
example 6
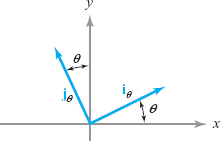
The vectors \({\bf i}_\theta=(\cos \theta){\bf i}+(\sin \theta){\bf j}\) and \({\bf j}_\theta=-(\sin \theta){\bf i}+(\cos \theta){\bf j}\) are orthogonal, because \[ {\bf i}_{\theta}\,{ \cdot}\, {\bf j}_{\theta}=-\kern-1pt\cos \theta \sin \theta+\sin\theta\cos\theta=0. \]
Here, \({\bf i}_{\theta}\) is the rotation of \({\bf i}\), \({\theta}^{\circ}\) counterclockwise. Also, \({\bf j}_{\theta}\) is the rotation of \({\bf j}\), \({\theta}^{\circ}\) counterclockwise (see Figure 1.36).
example 7
Let \({\bf a}\) and \({\bf b}\) be two nonzero orthogonal vectors. If \({\bf c}\) is a vector in the plane spanned by \({\bf a}\) and \({\bf b}\), then there are scalars \(\alpha\) and \(\beta\) such that \({\bf c}=\alpha {\bf a}+\beta {\bf b}\). Use the inner product to determine \(\alpha\) and \(\beta\) (see Figure 1.37).
25
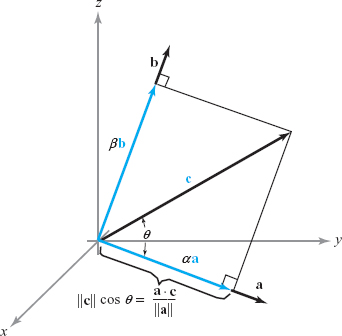
solution Taking the inner product of \({\bf a}\) and \({\bf c}\), we have \[ {\bf a}\,{ \cdot}\,{\bf c}= {\bf a} \,{ \cdot}\,(\alpha {\bf a}+\beta {\bf b}) =\alpha {\bf a}\,{ \cdot}\,{\bf a}+\beta {\bf a}\,{ \cdot}\,{\bf b}. \] Because \({\bf a}\) and \({\bf b}\) are orthogonal, \({\bf a}\,{ \cdot}\,{\bf b}=0\), and so \[ \alpha=\frac{{\bf a}\,{ \cdot}\,{\bf c}}{{\bf a}\,{ \cdot}\,{\bf a}}= \frac{{\bf a}\,{ \cdot}\,{\bf c}} {\|{\bf a}\|^2}. \] Similarly, \[ \beta=\frac{{\bf b}\,{ \cdot}\,{\bf c}}{{\bf b}\,{ \cdot}\,{\bf b}}= \frac{{\bf b}\,{ \cdot}\,{\bf c}} {\|{\bf b}\|^2}. \]
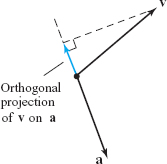
Orthogonal Projection
In the preceding example, the vector \(\alpha {\bf a}\) is called the projection of \({\bf c}\) along \({\bf a}\), and \(\beta {\bf b}\) is its projection along \({\bf b}\). Let us formulate this idea more generally. If \({\bf v}\) is a vector, and \(l\) is the line through the origin in the direction of a vector \({\bf a}\), then the orthogonal projection of \({\bf v}\) on \({\bf a}\) is the vector p whose tip is obtained by dropping a perpendicular line to \(l\) from the tip of \({\bf v}\), as in Figure 1.38.
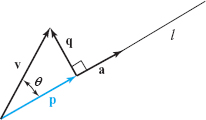
Referring to the figure, we see that \({\bf p}\) is a multiple of \({\bf a}\) and that \({\bf v}\) is the sum of \({\bf p}\) and a vector \({\bf q}\) perpendicular to \({\bf a}\). Thus, \[ {\bf v}=c {\bf a}+{\bf q}, \] where \({\bf p}=c{\bf a}\) and \({\bf a}\,{ \cdot}\,{\bf q}=0\). Taking the dot product of \({\bf a}\) with both sides of \({\bf v}=c{\bf a}+{\bf q}\), we find \({\bf a}\,{ \cdot}\,{\bf v}=c{\bf a}\,{ \cdot}\,{\bf a}\), so \(c=({\bf a}\,{ \cdot}\,{\bf v})/({\bf a}\,{ \cdot}\,{\bf a})\), and hence \[ {\bf p}=\frac{{\bf a}\,{ \cdot}\,{\bf v}}{\|{\bf a}\|^2}\,{\bf a}. \]
26
The length of \({\bf p}\) is \[ \|{\bf p}\|=\frac{|{\bf a}\,{ \cdot}\,{\bf v}|}{\|{\bf a}\|^2}\,\|{\bf a}\|=\frac{|{\bf a}\,{ \cdot}\,{\bf v}|}{\|{\bf a}\|} =\|{\bf v}\|\cos\theta. \]
Orthogonal Projection
The orthogonal projection of \({\bf v}\) on \({\bf a}\) is the vector \[ {\bf p}=\frac{{\bf a}\,{ \cdot}\,{\bf v}}{\|{\bf a}\|^2}\,{\bf a}. \]
example 8
Find the orthogonal projection of \({\bf i}+{\bf j}\) on \({\bf i}-2{\bf j}\).
solution With \({\bf a}={\bf i}-2{\bf j}\) and \({\bf v}={\bf i}+{\bf j}\), the orthogonal projection of \({\bf v}\) on \({\bf a}\) is \[ \frac{{\bf a}\,{ \cdot}\,{\bf v}}{{\bf a}\,{ \cdot}\,{\bf a}}\,{\bf a}=\frac{1-2}{1+4}\,({\bf i}-2{\bf j})=-\frac{1}{5}\,({\bf i}-2{\bf j}) \] (see Figure 1.39).
The Triangle Inequality
A useful consequence of the Cauchy–Schwarz inequality, which is called the triangle inequality, relates the lengths of vectors \({\bf a}\) and \({\bf b}\) and of their sum \({\bf a}+{\bf b}\). Geometrically, the triangle inequality says that the length of any side of a triangle is no greater than the sum of the lengths of the other two sides (see Figure 1.40).
Theorem 2 Triangle Inequality
For vectors \({\bf a}\) and \({\bf b}\) in space}, \[ \|{\bf a}+{\bf b}\|\leq \|{\bf a}\|+\|{\bf b}\|. \]
proof
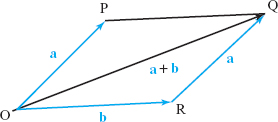
While this result may be clear geometrically, it is useful to give a proof using the Cauchy–Schwarz inequality, as it will generalize to n-dimensional vectors. We consider the square of the left-hand side: \[ \|{\bf a} +{\bf b}\|^2=({\bf a}+{\bf b})\,{ \cdot}\,({\bf a}+{\bf b})= \|{\bf a}\|^2+2{\bf a}\,{ \cdot}\,{\bf b}+\|{\bf b}\|^2. \]
27
By the Cauchy–Schwarz inequality, we have \[ \|{\bf a}\|^2+2{\bf a}\,{ \cdot}\,{\bf b}+\|{\bf b}\|^2 \leq \|{\bf a}\|^2+2\|{\bf a}\|\|{\bf b}\|+\|{\bf b}\|^2 = (\|{\bf a}\|+\|{\bf b}\|)^2. \] Thus, \[ \|{\bf a}+{\bf b}\|^2\leq (\|{\bf a}\|+\|{\bf b}\|)^2; \] taking square roots proves the result.
example 9
- (a) Verify the triangle inequality for \({\bf a}={\bf i}+{\bf j}\) and \({\bf b}=2{\bf i}+{\bf j}+{\bf k}\).
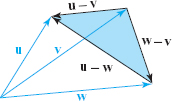
- (b) Prove that \(\|{\bf u}-{\bf v}\|\leq \|{\bf u}-{\bf w}\|+\|{\bf w}-{\bf v}\|\) for any vectors \({\bf u},{\bf v}\), and \({\bf w}\). Illustrate with a figure in which \({\bf u},{\bf v}\), and \({\bf w}\) have the same base point.
solution
- (a) We have \({\bf a}+{\bf b}=3{\bf i}+2{\bf j}+{\bf k}\), so \(\|{\bf a}+{\bf b}\|= \sqrt{9+4+1}=\sqrt{14}\). On the other hand, \(\|{\bf a}\|=\sqrt{2}\) and \(\|{\bf b}\|=\sqrt{6}\), so the triangle inequality asserts that \(\sqrt{14}\leq\sqrt{2}+\sqrt{6}\). The numbers bear this out: \(\sqrt{14}\approx 3.74\), while \(\sqrt{2}+\sqrt{6}\approx 1.41+ 2.45=3.86\).
- (b) We find that \({\bf u}-{\bf v}=({\bf u}-{\bf w})+({\bf w}-{\bf v})\), so the result follows from the triangle inequality with \({\bf a}\) replaced by \({\bf u}-{\bf w}\) and \({\bf b}\) replaced by \({\bf w}-{\bf v}\). Geometrically, we are considering the shaded triangle in Figure 1.41.
Physical Applications of Vectors
A simple example of a physical quantity represented by a vector is a displacement. Suppose that, on a part of the earth’s surface small enough to be considered flat, we introduce coordinates so that the \(x\) axis points east, the \(y\) axis points north, and the unit of length is the kilometer. If we are at a point P and wish to get to a point Q, the displacement vector \({\bf d}=\overrightarrow{\rm PQ\vphantom{^\prime}}\) joining P to Q tells us the direction and distance we have to travel. If \(x\) and \(y\) are the components of this vector, the displacement of P to Q is “\(x\) kilometers east, \(y\) kilometers north.”
example 10
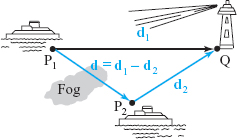
Suppose that two navigators who cannot see one another but can communicate by radio wish to determine the relative position of their ships. Explain how they can do this if they can each determine their displacement vector to the same lighthouse.
solution Let P\(_1\) and P\(_2\) be the positions of the ships, and let Q be the position of the lighthouse. The displacement of the lighthouse from the \(i\)th ship is the vector \({\bf d}_i\) joining P\(_i\) to Q. The displacement of the second ship from the first is the vector \({\bf d}\) joining P\(_1\) to P\(_2\). We have \({\bf d}+{\bf d}_2={\bf d}_1\) (Figure 1.42), and so \({\bf d}={\bf d}_1-{\bf d}_2\). That is, the displacement from one ship to the other is the difference between the displacements from the ships to the lighthouse.
28
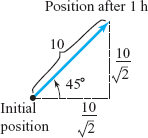
We can also represent the velocity of a moving object as a vector. For the moment, we will consider only objects moving at uniform speed along straight lines. Suppose, for example, that a boat is steaming across a lake at 10 kilometers per hour (km/h) in the northeast direction. After 1 hour of travel, the displacement is \((10/\sqrt{2},10/\sqrt{2})\approx (7.07,7.07)\); see Figure 1.43.
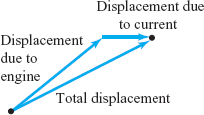
The vector whose components are \((10/\sqrt{2},10/\sqrt{2})\) is called the velocity vector of the boat. In general, if an object is moving uniformly along a straight line, its velocity vector is the displacement vector from the position at any moment to the position \(1\) unit of time later. If a current appears on the lake, moving due eastward at 2 km/h, and the boat continues to point in the same direction with its engine running at the same rate, its displacement after 1 hour will have components given by \((10/\sqrt{2}+2,10/\sqrt{2})\); see Figure 1.44. The new velocity vector, therefore, has components \((10/\sqrt{2}+2,10/\sqrt{2})\). We note that this is the sum of the original velocity vector \((10/\sqrt{2},10/\sqrt{2})\) of the boat and the velocity vector (2, 0) of the current.
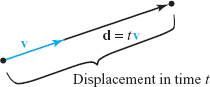
Displacement and Velocity
If an object has a (constant) velocity vector \({\bf v}\), then in \(t\) units of time the resulting displacement vector of the object is \({\bf d}=t{\bf v}\); thus, after time \(t = 1\), the displacement vector equals the velocity vector. See Figure 1.45.
example 11
A bird is flying in a straight line with velocity vector \(10{\bf i}+6{\bf j}+{\bf k}\) (in kilometers per hour). Suppose that \((x,y)\) are its coordinates on the ground and \(z\) is its height above the ground.
- (a) If the bird is at position \((1, 2, 3)\) at a certain moment, what is its location 1 hour later? 1 minute later?
- (b) How many seconds does it take the bird to climb \(10\) meters\(?\)
solution
- (a) The displacement vector from (1, 2, 3) after 1 hour is given by \(10{\bf i}+6{\bf j}+{\bf k}\), so the new position is \((1, 2, 3) + (10, 6, 1)=(11, 8, 4)\). After 1 minute, the displacement vector from \((1,2,3)\) is \(\frac{1}{60}(10{\bf i}+ 6{\bf j} + {\bf k})=\frac{1}{6}{\bf i}+ \frac{1}{10}{\bf j}+\frac{1}{60}{\bf k}\), and so the new position is \((1,2,3)+(\frac{1}{6},\frac{1}{10},\frac{1}{60}) =(\frac{7}{6},\frac{21}{10},\frac{181}{60})\).
- (b) After \(t\) seconds \(({=t}/3600\) hours), the displacement vector from (1, 2, 3) is \((t/3600)\) \((10{\bf i}+6{\bf j}+{\bf k})=(t/360){\bf i}+(t/600){\bf j} +(t/3600) {\bf k}\). The increase in altitude is the \(z\) component, namely, \(t/3600\). This will equal 10 m \(({=\frac{1}{100}}\hbox{ km})\) when \(t/3600=\frac{1}{100}\), that is, when \(t=36\hbox{ s}\).
29
example 12
Physical forces have magnitude and direction and may thus be represented by vectors. If several forces act at once on an object, the resultant force is represented by the sum of the individual force vectors. Suppose that forces \({\bf i}+{\bf k}\) and \({\bf j}+{\bf k}\) are acting on a body. What third force F must we impose to counteract the two–that is, to make the total force equal to zero?
solution The force \({\bf F}\) should be chosen so that \(({\bf i}+{\bf k})+ (\,{\bf j}+{\bf k})+{\bf F}={\bf 0}\); that is, \({\bf F}=-({\bf i}+{\bf k})-(\kern1pt{\bf j}+{\bf k})=-{\bf i}-{\bf j}-2{\bf k}\). (Recall that 0 is the zero vector, the vector whose components are all zero.)