The word mathematics derives from the Greek word mathema, meaning knowledge, cognition, understanding, or perception, suggesting that the study of what we now call mathematics began by asking questions about the world. In fact, the historical evidence suggests that mathematics began about 2700 years ago as an attempt to comprehend nature. Unfortunately, in most mathematical expositions, historical motivations and contexts are often sacrificed. In this new edition, the authors continue to address this problem by including the discussion of historical and contextual material where appropriate. Therefore, before we dive into the mathematics of Vector Calculus, we briefly discuss the development of mathematics prior to and including the discovery of calculus.

It is generally acknowledged that mathematics developed in the seventh and sixth centuries B.C., somewhat after the Greeks had developed a uniform alphabet. This is not to say, however, that mathematical knowledge did not exist before the Greeks. In fact, the Egyptians and Babylonians knew many empirical facts centuries before the rise of the Greek civilization. For example, they could solve quadratic equations, compute the areas of certain geometric figures, such as squares, rectangles, and triangles, and they possessed a reasonably good formula for the area of a circle, using the value of 3.16 for π. They also knew how to compute certain volumes like the size of cubes, rectangles, rectangular solids, cones, cylinders, and (not surprisingly) pyramids. The ancients were also acquainted with the Pythagorean theorem (at least empirically).

The Greeks, who settled throughout the Mediterranean, must have played an important role in preserving and spreading the mathematical knowledge of the Egyptians and the Babylonians. However, the Greeks were aware that there were different formulas for the same area or volumes. For example, the Babylonians had one formula for the volume of a frustum of a pyramid with a square base, and the Egyptians had another (see Figure 1).

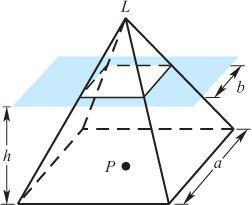
It is not surprising that the Egyptians (with the experience in pyramid construction) had the correct formula. Now, given two formulas, it was clear that only one could be correct. But how could one decide such an answer? Certainly it is not a question for debate, as would be the question of the quality of works of art. It is likely that the necessity to determine the answers to such questions is what led to the development of mathematical proof and to the method of deductive reasoning.

xiv

The person usually credited for the invention of rigorous mathematical proof was a merchant named Thales of Miletus (624–548 B.C.). It is Thales who is said to be the creator of Greek geometry, and it was this geometry (earth measure) as an abstract mathematical theory (rather than a collection of empirical facts) supported by rigorous deductive proofs that was one of the turning points of scientific thinking. It led to the creation of the first mathematical model for physical phenomena.

For example, one of the most beautiful geometric theories developed during antiquity was that of conic sections. See Figure 2.

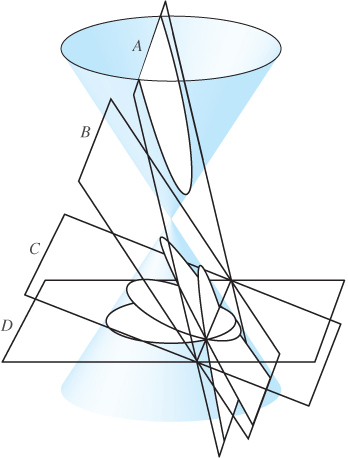
Conics include the straight line, circle, ellipse, parabola, and hyperbola. Their discovery is attributed to Menaechmus, a member of the school of the great Greek philosopher Plato. Plato, a student of Socrates, founded his school The Academy (see Figure 3) in a sacred area of the ancient city of Athens, called Hekadameia (after the hero Hekademos). All later academies obtained their name from this institution, which existed without interruption for about 1000 years until it was dissolved by the Roman Emperor Justinian in 529 C.E.

xv

Plato suggested the following problem to his students:

Explain the motion of the heavenly bodies by some geometrical theory.

Why was this a question of interest and puzzlement for the Greeks? Observed from the Earth, these motions appear to be quite complicated. The motions of the sun and the moon can be roughly described as circular with constant speed, but the deviations from the circular orbit were troublesome to the Greeks and they felt challenged to find an explanation for these irregularities. The observed orbits of the planets are even more complicated, because as they go through a revolution, they appear to reverse direction several times.

The Greeks sought to understand this apparently wild motion by means of their geometry. Eudoxus, Hipparchus, and then Apollonius of Perga (262–190 B.C.) suggested that the celestial orbits could be explained by combinations of circular motion (that is, through the construction of curves called epicycles traced out by circles moving on other circles). This idea was to become the most important astronomical theory of the next two thousand years. This theory, known by us through the writings of the Greek astronomer Ptolemy of Alexandria, ultimately becomes known as the “Ptolemaic theory.” See Figures 4 and 5.

Most of Greek geometry was codified by Euclid in his Elements (of Mathematics). Actually the Elements consist of thirteen books, in which Euclid collected most of the mathematical knowledge of his age (circa 300 B.C.), transforming it into a lucid, logically developed masterpiece. In addition to the Elements, some of Euclid’s other writings were also handed down to us, including his Optics and the Catoptrica (theory of mirrors).

The success of Greek mathematics had a profound effect on views of nature. The Platonists, or followers of Plato, distinguished between the world of ideas and the world of physical objects. Plato was the first to propose that ultimate truth or understanding could not come from the material world, which is constantly subject to change, but only from mathematical models or constructs. Thus, infallible knowledge could be attained only through mathematics. Plato not only wished to use mathematics in the study of nature, but he actually went so far as to attempt to substitute mathematics for nature. For Plato, reality lies only within the realm of ideas, especially mathematical ideas.

xvi

Not everyone in antiquity agreed with this point of view. Aristotle, a student of Plato, criticized Plato’s reduction of science to the study of mathematics. Aristotle thought that the study of the material world was one’s primary source of reality. Despite Aristotle’s critique, the view that mathematical laws governed the universe took a firm hold on classical thought. The search for the mathematical laws of nature was underway.

After the death of Archimedes in 212 B.C., Greek civilization went into a period of slow decline. The final blow to Greek civilization came in 640 A.D. with the Moslem conquest of Egypt. The remaining Greek texts housed in the great library in Alexandria were burned. Those scholars who survived migrated to Constantinople (now part of Turkey), which had become the capitol of the Eastern Roman Empire. It was in this great city that what survived of Greek civilization was preserved for its rediscovery by European civilization some five hundred years later.

xvii

Mathematical activity did not, however, cease with the decline of Greek civilization. In the middle of the sixth century, somewhere in the Ganges Valley in India, our modern system of numeration evolved. The Indians developed a number system based on ten, with ten rather abstract symbols from zero to nine looking “roughly” as they do today. They developed rules for addition, multiplication, and division (as we have today), a system infinitely superior to the Roman abacus, which was used (by a special class of servants called arithmeticians) throughout Europe until the fifteenth century. See Figure 6.

After the fall of Egypt, came the rise of Arab civilization centered in Baghdad. Scholars from Constantinople and India were invited to study and to share their knowledge. It was through these contacts that the Arabs came to acquire the learning of the ancients as well as the newly discovered Indian system of numeration. See Figure 7.

xviii

It was the Arabs who gave us the name Algebra, which comes from the book by the astronomer Mohammed ibn Musa al-Khuwarizmi titled “Al-Jabr w’al muqabola,” which means “restoring” or “balancing” (equations). Al-Khuwarizmi is also responsible for a second profoundly influential book entitled “Kitab al jami’ wa’l tafriq bi hisab al hind” (Indian Technique of Addition and Subtraction), which described and clarified the Indian decimal place value system.

The decline of Arab civilization coincided with the rise of European civilization. The dawn of the modern age began when Richard the Lionhearted reached the walls of Jerusalem. From approximately 1192 through around 1270, the Christian knights brought the learning of the “infidels” back to Europe. Around 1200–1205, Leonardo of Pisa (also known as Fibonacci), who had traveled extensively in Africa and Asia Minor, wrote his interpretation (in Latin) of Arabic and Greek mathematics. His historic texts brought the work of al-Khuwarizmi and Euclid to the attention of a large audience in Europe.

Around 1450 Johann Gutenberg invented the printing press with movable type. This, combined with the advent of linen and cotton paper obtained from the Chinese, dramatically increased the rate of the dissemination of knowledge. The steep rise in trade and manufacturing fueled the growth of wealth and dramatic change in European societies from feudal to city-states. In Italy, the mother of the Renaissance, we see the rise of extraordinarily wealthy states such as Venice under the Doges and Florence under the Medicis.

The needs of the rising merchant class accelerated the adoption of the Indian system of numeration. The teachings of the Catholic Church, which rested on absolute authority and dogma, began to be challenged by the ideas of Plato. From Plato, scholars learned that the world was rational and could be understood, and that the means of understanding nature was through mathematics. But this sharply contradicted the teachings of the church, which taught that God designed the universe. The only possible resolution of this apparent contradiction was that “God designed the universe mathematically” or that “God is a mathematician.”

It is perhaps surprising how much this point of view inspired the work of many sixteenth- to eighteenth-century mathematicians and scientists. For if this were indeed the case, then by understanding the mathematical laws of the universe, one could come closer to an understanding of the Creator himself. Believe it or not, this point of view survives to this day. The following is a quote from Paul Dirac, a Nobel Prize–winning physicist and a creator of modern quantum mechanics.

It seems to be one of the fundamental features of nature that fundamental physical laws are described in terms of a mathematical theory of great beauty and power, needing quite a high standard of mathematics for one to understand it. You may wonder: Why is nature constructed along these lines? One can only answer that our present knowledge seems to show that nature is so constructed. We simply have to accept it. One could perhaps describe the situation by saying that God is a mathematician of a very high order, and He used very advanced mathematics in constructing the universe. Our feeble attempts at mathematics enable us to understand a bit of the universe, and as we proceed to develop higher and higher mathematics we can hope to understand the universe better.

Mathematics began to see further advances and applications. In the sixteenth and seventeenth centuries, al-Khuwarizmi’s algebra was significantly advanced by Cardano, Vieta, and Descartes. The Babylonians had solved the quadratic equation, but now two thousand years later, del Ferro and Tartaglia solved the cubic equation, which in turn led to the discovery of imaginary numbers. These imaginary numbers were later to play a fundamental role, as we shall see, in the development of vector calculus. In the early seventeenth century, Descartes, perhaps motivated by the grid technique used by Italian fresco painters to locate points on a wall or canvas, created, in a moment of great mathematical inspiration, coordinate (or analytic) geometry. This new mathematical model enables one to reduce Euclid’s geometry to algebra and provides a precise and quantitative method to describe and calculate with space curves and surfaces.

xix

Early on, Archimedes’ great work in statics and equilibrium (centers of gravity, the principle of the lever—which we study in this book) was absorbed and improved upon, leading to dramatic engineering achievements. In a building spree that remains astonishing to this day, engineering advances made possible the rise of an incredible number of cathedrals throughout Europe, including the stunning Duomo in Florence, Notre Dame in Paris, and the Great Cathedral in Cologne, to mention a few. See Figure 8.

However, as in Greek times, it was astronomy that was to give mathematics its greatest impetus. It is not surprising that the Greek astronomers placed the Earth and not the sun at the center of our universe, because on a daily basis we see the sun both rise and set. Still, it is interesting to ask if the Greeks, who were such marvelous thinkers, at least tested the heliocentric theory, which places the sun at the center of the universe. In fact, they did. In the third century B.C., Aristarchus of Samus taught that the Earth and other planets move in circular orbits around a fixed sun. His hypotheses were, for several reasons, rejected. First, the opposing astronomers reasoned that if the Earth were indeed moving, one should be able to sense it. Second, how would objects, circulating with us, be able to stay on a moving Earth? Third, why are the clouds not lagging behind the moving Earth?

Such arguments were to be used again in the sixteenth century against the Polish astronomer Nicolas Copernicus (see Figure 9), who in 1543 introduced the heliocentric theory (the planets move in orbit around the sun). His book Revolutionibus Orbium Coelestium (On the Revolution of the Heavenly Orbits) was to initiate the “Copernican revolution” in science and to give the world a new word, revolutionary.

xx

In 1619, the German astronomer Johannes Kepler (see Figure 10), using the astronomical calculations of the Danish astronomer Tycho Brahe, showed that the planetary orbits were in fact elliptical, the same ellipses that the Greeks had studied as abstract forms some 2000 years earlier (see Figure 11).

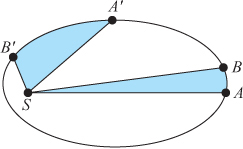
But Kepler’s law of elliptical orbits was only one of three laws he discovered governing planetary motion. Kepler’s second law states that if a planet moves from a point A to another point B in a certain amount of time T, and also moves from A^′ to B^′ in the same time, and if S is a focus of the orbital ellipse, then the sections SAB are SA^′B^′ have equal areas (see Figure 12). Kepler’s third law was that the square of time T a planetary body requires to complete an orbit is proportional to a³, where a is the great axis of the elliptical orbit. In equation form, T² = K a³, where K is some constant (we shall derive this law for circular orbits in Chapter 4).

Profound as these observations were, an explanation of why these laws held was lacking. However, by the middle of the seventeenth century, it was fully understood that a change of velocity requires the action of forces, but how these forces influenced motion was not at all clear. In 1674 Robert Hooke, in an attempt to explain Kepler’s laws, assumed the existence of an attractive force the sun must exert on the planets, a force that decreased with planetary distance. Hooke’s theory, however, was only qualitative.

What was also seriously lacking was a quantitative, precise definition of both velocity and acceleration. This was ultimately solved by the invention of calculus by both Isaac Newton and Gottfried Wilhelm Leibniz (see Figure 13). Hooke was never able to achieve an understanding of the profound ideas behind the infinitesimal calculus. However, during the period of 1679–1680 Hooke discussed his ideas with Newton, including his conjecture that the force the sun exerts on the planets was actually inversely proportional to the square of the planetary distance.

After Sir Christopher Wren, amateur astronomer, architect of the city of London and London’s magnificent St. Paul’s Cathedral, issued a public challenge to “theoretically determine” the orbits of the planets, Isaac Newton took a serious interest in the problem. Perhaps acting on rumors, the great British astronomer Edmund Halley (1656–1743) in August 1684 visited Newton in Cambridge and asked him directly what the orbit of a planet would be under an inverse square force. Newton answered that it had to be an ellipse. As the stunned Halley asked him how he knew this, Newton’s famous reply was “Why I have calculated it.” Halley ultimately urged Newton to publish his results as a book, and these appeared in 1686 in Newton’s now legendary Principia. See Figure 15.

xxi

This book, often and justly referred to as the foundation of modern science, had an immediate dramatic impact. Alexander Pope wrote:

In Figure 14, we see Newton holding open a copy of his Principia.

Although Newton did not use calculus in the Principia, convincing arguments have been put forward that Newton originally used his calculus to derive the trajectories of the planetary orbits from the inverse square law.^* The Principia provided profound evidence that the universe, as the early Greeks had understood, was indeed designed mathematically. Incidentally, it was Newton who first conceptualized force as a vector, although he provided no formal definition of what a vector was. Such a formal definition had to wait for William Rowan Hamilton, a century and a half after the Principia.

xxii

The invention of the calculus and the subsequent development of vector calculus was the true beginning of modern science and technology, which has changed our world so dramatically. From the mathematics of Newton’s mechanics to the profound intellectual constructs of Maxwell’s electrodynamics, Einstein’s relativity, and Heisenberg’s and Schr¨odinger’s quantum mechanics, we have seen the discoveries of radio, television, wireless communications, flight, computers, space travel, and countless engineering marvels.

Underlying all these developments was mathematics, an exciting adventure of the mind and a celebration of the human spirit. It is in this context that we begin our account of vector calculus.

xxiii

We assume that students have studied the calculus of functions of a real variable, including analytic geometry in the plane. Some students may have had some exposure to matrices as well, although what we shall need is given in Sections 1.3 and 1.5.

We also assume that students are familiar with functions of elementary calculus, such as sin x, cos x, e^x, and log x (we write log x or ln x for the natural logarithm, which is sometimes denoted log_ex). Students are expected to know, or to review as the course proceeds, the basic rules of differentiation and integration for functions of one variable, such as the chain rule, the quotient rule, integration by parts, and so forth.

We now summarize the notations to be used later. Students can read through these quickly now, then refer to them later if the need arises.

The collection of all real numbers is denoted ℝ. Thus ℝ includes the integers,…, −3, −2, −1, 0, 1, 2, 3, …; the rational numbers, p/q, where p and q are integers (q ≠ 0); and the irrational numbers, such as , π, and e. Members of ℝ may be visualized as points on the real-number line, as shown in Figure P.1.

When we write a ∈ ℝ we mean that a is a member of the set ℝ, in other words, that a is a real number. Given two real numbers a and b with a < b (that is, with a less than b), we can form the closed interval [a, b], consisting of all x such that a ≤ x ≤ b, and the open interval (a, b), consisting of all x such that a < x < b. Similarly, we can form half-open intervals (a, b] and [a, b) (Figure P.2).

The absolute value of a number a ∈ ℝ is written |a| and is defined as

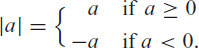
For example, |3| = 3, |−3| = 3, |0| = 0, and |−6| = 6. The inequality |a + b| ≤ |a| + |b| always holds. The distance from a to b is given by |a − b|. Thus, the distance from 6 to 10 is 4 and from −6 to 3 is 9.

If we write A ⊂ ℝ, we mean A is a subset of ℝ. For example, A could equal the set of integers {…, −3, −2, −1, 0, 1, 2, 3, …}. Another example of a subset of ℝ is the set ℚ of rational numbers. Generally, for two collections of objects (that is, sets) A and B, A ⊂ B means A is a subset of B; that is, every member of A is also a member of B.

The symbol A ∪ B means the union of A and B, the collection whose members are members of either A or B (or both). Thus,

{…, −3, −2, −1, 0} ∪ {−1, 0, 1, 2, …} = {…, −3, −2, −1, 0, 1, 2, …}.

xxiv

Similarly, A ∩ B means the intersection of A and B; that is, this set consists of those members of A and B that are in both A and B. Thus, the intersection of the two sets on the preceding page is {−1, 0}.

We shall write A\B for those members of A that are not in B. Thus,

{…, −3, −2, −1, 0}\{−1, 0, 1, 2, …} = {…, −3, −2}.

We can also specify sets as in the following examples:

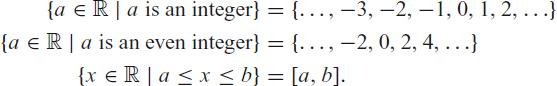
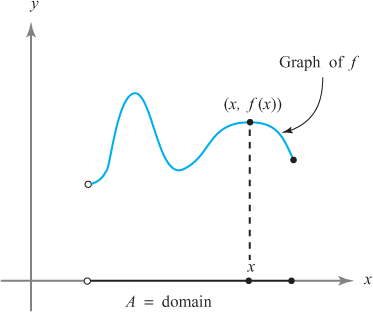
A function f: A → B is a rule that assigns to each a ∈ A one specific member f (a) of B. We call A the domain of f and B the target of f. The set {f (x) | x ∈ A} consisting of all the values of f (x) is called the range of f. Denoted by f (A), the range is a subset of the target B. It may be all of B, in which case f is said to be onto B. The fact that the function f sends a to f (a) is denoted by a ↦ f (a). For example, the function f (x) = x³/(1 − x) that assigns the number x³/(1 − x) to each x ≠ 1 in ℝ can also be defined by the rule x ↦ x³/(1 − x). Functions are also called mappings, maps, or transformations. The notation f : A ⊂ ℝ → ℝ means that A is a subset of ℝ and that f assigns a value f (x) in ℝ to each x ∈ A. The graph of f consists of all the points (x, f (x)) in the plane (Figure P.3).

The notation 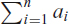means a₁ +…+ a_n, where a₁, …, a_n are given numbers. The sum of the first n integers is

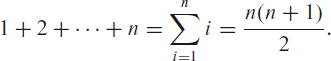
The derivative of a function f (x) is denoted f′(x), or

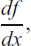
xxv

and the definite integral is written

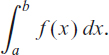
If we set y = f (x), the derivative is also denoted by

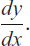
Readers are assumed to be familiar with the chain rule, integration by parts, and other basic facts from the calculus of functions of one variable. In particular, they should know how to differentiate and integrate exponential, logarithmic, and trigonometric functions. Short tables of derivatives and integrals, which are adequate for the needs of this text, are printed at the front and back of the book.

The following notations are used synonymously: e^x = exp x, ln x = log x, and sin⁻¹ x = arcsin x.

The end of a proof is denoted by the symbol , while the end of an example or remark is denoted by the symbol .

xxvi

^* We shall study the problem of planetary orbits in Section 4.1 and further in the Internet supplement.