11.6 A Survey of Quadratic Surfaces
Quadratic or quadric surfaces are the surface analogs of conic sections. Understanding quadratic surfaces, which, after planes, are the simplest examples of surfaces, will help us gain an understanding of one of the basic objects in the study of vector calculus. Recall that a conic section is a curve in \(\textbf{R}^2\) defined by a quadratic equation in two variables. A quadric surface is defined by a quadratic equation in three variables: \begin{equation} Ax^2+By^2+Cz^2+Dxy+Eyz+Fzx+ax+by+cz+d=0\tag{1} \end{equation}
Like conic sections, quadric surfaces are classified into a small number of types. When the coordinate axes are chosen to coincide with the axes of the quadric, the equation of the quadric has a simple form. The quadric is then said to be in standard position. In standard position, the coefficients \(D\), \(E\), \(F\) are all zero and the linear part \((ax+by+cz+d)\) also reduces to just one term. In this short survey of quadric surfaces, we restrict our attention to quadrics in standard position.
Note
To ensure that Eq.(1) is genuinely quadratic, we assume that the degree-2 coefficients \(A, B, C, D, E, F\) are not all zero.
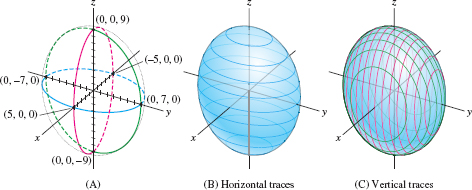
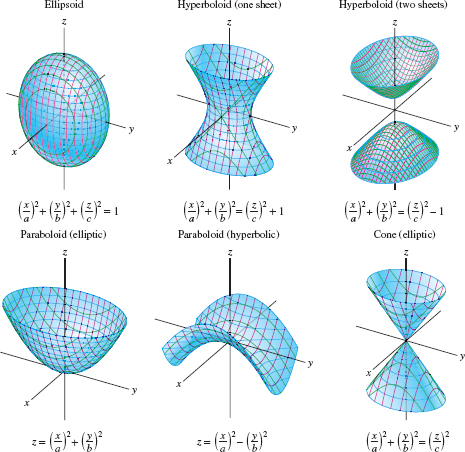
The surface analogs of ellipses are the egg-shaped ellipsoids (Figure 11.106). In standard form, an ellipsoid has the equation \[ \boxed{\bbox[#fef7e5,5pt]{\textbf{Ellipsoid}\qquad \left(\frac{x}a\right)^2+\left(\frac{y}b\right)^2+\left(\frac{z}c\right)^2=1 }}\]
For \(a=b=c\), this equation is equivalent to \(x^2+y^2+z^2=a^2\) and the ellipsoid is a sphere of radius \(a\).
Surfaces are often represented graphically by a mesh of curves called traces, obtained by intersecting the surface with planes parallel to one of the coordinate planes (Figure 11.107). Algebraically, this corresponds to freezing one of the three variables (holding it constant). For example, the intersection of the horizontal plane \(z=z_0\) with the surface is a horizontal trace curve.
706
EXAMPLE 1 The Traces of an Ellipsoid
Describe the traces of the ellipsoid \[ \left(\frac{x}5\right)^2 + \left(\frac{y}7\right)^2 + \left(\frac{z}9\right)^2 = 1 \]
Solution First we observe that the traces in the coordinate planes are ellipses (Figure 11.108): \begin{align*} &\textrm{\(xy\)-trace (set \(z=0\), blue in figure):}&\qquad &\left(\frac{x}5\right)^2 + \left(\frac{y}7\right)^2 = 1\\ &\textrm{\(yz\)-trace (set \(x=0\), green in figure):}&\qquad & \left(\frac{y}7\right)^2 + \left(\frac{z}9\right)^2 = 1\\ &\textrm{\(xz\)-trace (set \(y=0\), red in figure):}&\qquad &\left(\frac{x}5\right)^2 + \left(\frac{z}9\right)^2 = 1 \end{align*}
In fact, all the traces of an ellipsoid are ellipses. For example, the horizontal trace defined by setting \(z=z_0\) is the ellipse [Figure 11.108] \[ \textrm{Trace at height \(z_0\):}\quad \left(\frac{x}5\right)^2 + \left(\frac{y}7\right)^2 + \left(\frac{z_0}9\right)^2 = 1\qquad \textrm{or}\qquad \frac{x^2}{25} + \frac{y^2}{49} = \underbrace{1 - \frac{z_0^2}{81}}_{\textrm{A constant}} \]
The trace at height \(z_0=9\) is the single point \((0,0,9)\) because \({{x^2}/{25} + {y^2}/{49}=0}\) has only one solution: \(x=0, y=0\). Similarly, for \(z_0 = -9\) the trace is the point \((0,0,-9)\). If \(|z_0| \gt 9\), then \(1-z_0^2/81 \lt 0\) and the plane lies above or below the ellipsoid. The trace has no points in this case. The traces in the vertical planes \(x=x_0\) and \(y=y_0\) have a similar description [Figure 11.108].
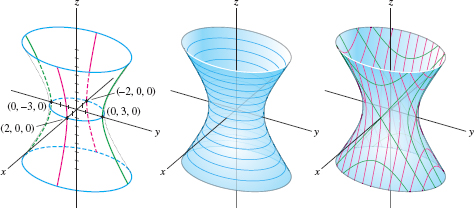
The analogs of the hyperbolas are the hyperboloids, which come in two types, depending on whether the surface has one or two components. We refer to these types as hyperboloids of one or two sheets (Figure 11.109). Their equations in standard position are
\(\boxed{\bbox[#fef7e5,5pt]{ \textbf{Hyperboloid of One Sheet:} \displaystyle{ \ \ \left(\frac{x}a\right)^2 + \left(\frac{y}b\right)^2 = \left(\frac{z}c\right)^2 + 1} \\ \textbf{Hyperboloid of Two Sheets:} \displaystyle{ \ \ \left(\frac{x}a\right)^2 + \left(\frac{y}b\right)^2 = \left(\frac{z}c\right)^2 -1} } \tag{2}}\)
707
Notice that a hyperboloid of two sheets does not contain any points whose \(z\)-coordinate satisfies \(-c \lt z \lt c\) because the right-hand side \({\left(\frac{z}c\right)^2 -1}\) is then negative, but the left-hand side of the equation is greater than or equal to zero.
EXAMPLE 2 The Traces of a Hyperboloid of One Sheet
Determine the traces of the hyperboloid \({ \left(\frac{x}2\right)^2 + \left(\frac{y}3\right)^2 = \left(\frac{z}4\right)^2 + 1}\).
Solution The horizontal traces are ellipses and the vertical traces (parallel to both the \(yz\)-plane and the \(xz\)-plane) are hyperbolas (Figure 11.110): \begin{align*} &\textrm{Trace \(z=z_0\) (ellipse, blue in figure):}&\qquad&\left(\frac{x}2\right)^2 + \left(\frac{y}3\right)^2 = \left(\frac{z_0}4\right)^2 + 1\\ &\textrm{Trace \(x=x_0\) (hyperbola, green in figure):}&\qquad & \left(\frac{y}3\right)^2 - \left(\frac{z}4\right)^2 = 1-\left(\frac{x_0}2\right)^2\\ &\textrm{Trace \(y=y_0\) (hyperbola, red in figure):}&\qquad&\left(\frac{x}2\right)^2 - \left(\frac{z}4\right)^2 = 1 - \left(\frac{y_0}3\right)^2 \end{align*}
708
EXAMPLE 3 Hyperboloid of Two Sheets Symmetric about the \(y\)-axis
Show that \({ \left(\frac{x}a\right)^2 + \left(\frac{z}c\right)^2 = \left(\frac{y}b\right)^2 - 1}\) has no points for \(-b \lt y \lt b\).
Solution This equation does not have the same form as Eq.(3) because the variables \(y\) and \(z\) have been interchanged. This hyperboloid is symmetric about the \(y\)-axis rather than the \(z\)-axis (Figure 11.111). The left-hand side of the equation is always \(\geq 0\). Thus, there are no solutions with \(|y| \lt b\) because the right-hand side is \({\left(\tfrac{y}b\right)^2-1 \lt 0}\). Therefore, the hyperboloid has two sheets, corresponding to \(y\ge b\) and \(y\le -b\).
The following equation defines an elliptic cone (Figure 11.112): \[\boxed{ \bbox[#fef7e5,5pt]{\textbf{Elliptic Cone:}\qquad\left(\frac{x}a\right)^2+\left(\frac{y}b\right)^2= \left(\frac{z}c\right)^2 }}\]
An elliptic cone may be thought of as a limiting case of a hyperboloid of one sheet in which we “pinch the waist” down to a point.
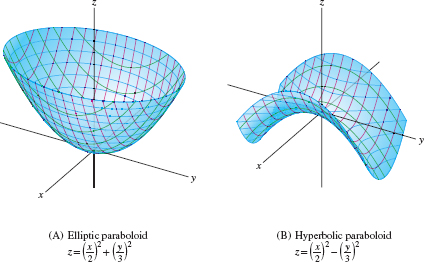
The third main family of quadric surfaces are the paraboloids. There are two types—elliptic and hyperbolic. In standard position, their equations are
\[ \boxed{\bbox[#fef7e5,25pt]{ \textbf{Elliptic Paraboloid:} \displaystyle{ \ \ z = \Big(\frac{x}a\Big)^2+\Big(\frac{y}b\Big)^2} \\ \textbf{Hyperbolic Paraboloid:} \displaystyle{ \ \ z = \Big(\frac{x}a\Big)^2 - \Big(\frac{y}b\Big)^2} \tag{3} }}\]
Let's compare their traces (Figure 11.113):
| Elliptic paraboloid | Hyperbolic paraboloid | |
| Horizontal traces | ellipses | hyperbolas |
| Vertical traces | upward parabolas | upward and downward parabolas |
709
Notice, for example, that for the hyperbolic paraboloid, the vertical traces \(x=x_0\) are downward parabolas (green in the figure) \[ \underbrace{z = -\left(\frac{y}b\right)^2 + \left(\frac{x_0}a\right)^2}_{\textrm{Trace \(x=x_0\) of hyperbolic paraboloid}} \]
whereas the vertical traces \(y=y_0\) are upward parabolas (red in the figure) \[ \underbrace{z = \left(\frac{x}a\right)^2 - \left(\frac{y_0}b\right)^2}_{\textrm{Trace \(y=y_0\) of hyperbolic paraboloid}} \]
Question 11.173 Section 11.6 Progress Check Question 1
The equation \(x^2-2y^2-z^2=1\) represents a quadratic surface. What kind?
| A. |
| B. |
| C. |
| D. |
| E. |
EXAMPLE 4 Alternative Form of a Hyperbolic Paraboloid
Show that \(z=4xy\) is a hyperbolic paraboloid by writing the equation in terms of the variables \(u=x+y\) and \(\textbf{v}=x-y\).
Solution Note that \(u+v=2x\) and \(u-v= 2y\). Therefore, \[ 4xy = (u+v)(u-v) = u^2-v^2 \]
and thus the equation takes the form \(z=u^2-v^2\) in the coordinates \(\{u,v,z\}\). The coordinates \(\{u,v,z\}\) are obtained by rotating the coordinates \(\{x,y,z\}\) by \(45^\circ\) about the \(z\)-axis (Figure 11.114).
Note
Paraboloids play an important role in the optimization of functions of two variables. The elliptic paraboloid in Figure 11.113 has a local minimum at the origin. The hyperbolic paraboloid is a “saddle shape” at the origin, which is an analog for surfaces of a point of inflection.
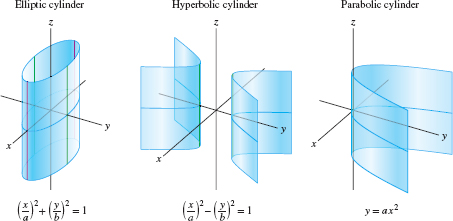
Further examples of quadric surfaces are the quadratic cylinders. We use the term cylinder in the following sense: Given a curve \(C\) in the \(xy\)-plane, the cylinder with base \(C\) is the surface consisting of all vertical lines passing through \(C\) (Figure 11.115).
Equations of cylinders involve just the two variables \(x\) and \(y\). The equation \(x^2 + y^2 = r^2\) defines a circular cylinder of radius \(r\) with the \(z\)-axis as central axis. Figure 11.116 shows a circular cylinder and three other types of quadratic cylinders.
The ellipsoids, hyperboloids, paraboloids, and quadratic cylinders are called nondegenerate quadratic surfaces. There are also a certain number of “degenerate” quadratic surfaces. For example, \(x^2 + y^2 + z^2 = 0\) is a quadric that reduces to a single point \((0,0,0)\), and \((x + y + z)^2 = 1\) reduces to the union of the two planes \(x + y + z = \pm 1\).
710
Question 11.174 Section 11.6 Progress Check Question 2
The equation \(x^2+2y^2=1\) represents a quadratic surface. What kind?
| A. |
| B. |
| C. |
| D. |
| E. |
Summary
- A quadric surface is a surface defined by a quadratic equation in three variables in which the coefficients \(A\)–\(F\) are not all zero: \[ Ax^2+By^2+Cz^2+Dxy+Eyz+Fzx+ax+by+cz+d=0 \]
- Quadric surfaces in standard position:
711
- A (vertical) cylinder is a surface consisting of all
vertical lines passing through a curve (called the base) in the
\(xy\)-plane. A quadratic cylinder is a cylinder whose base is a
conic section. There are three types: