11.4 A Review of Conic Sections (Optional)
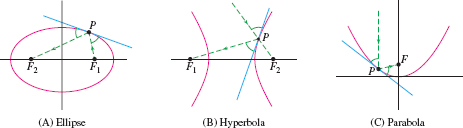
Three familiar families of curves—ellipses, hyperbolas, and parabolas—appear throughout mathematics and its applications. They are called conic sections because they are obtained as the intersection of a cone with a suitable plane (Figure 11.61). Our goal in this section is to derive equations for the conic sections from their geometric definitions as curves in the plane.
The conics were first studied by the ancient Greek mathematicians, beginning possibly with Menaechmus (c. 380–320 BCE) and including Archimedes (287–212 BCE) and Apollonius (c. 262–190 BCE).
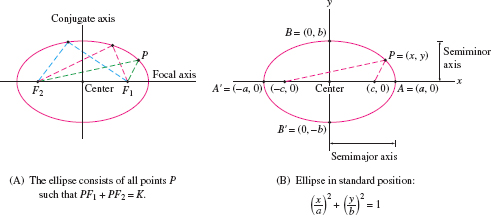
An ellipse is an oval-shaped curve [Figure 11.62] consisting of all points \(P\) such that the sum of the distances to two fixed points \(F_1\) and \(F_2\) is a constant \(K>0\): \begin{equation} PF_1 + PF_2 = K\tag{1} \end{equation}
The points \(F_1\) and \(F_2\) are called the foci (plural of “focus”) of the ellipse. Note that if the foci coincide, then Eq. (1) reduces to \(2PF_1=K\) and we obtain a circle of radius \(\frac12 K\) centered at \(F_1\).
We assume always that \(K\) is greater than the distance \(F_1F_2\) between the foci, because the ellipse reduces to the line segment \(\overline{F_1F_2}\) if \(K=F_1F_2\), and it has no points at all if \(K \lt F_1F_2\).
We use the following terminology:
- The midpoint of \(\overline{F_1F_2}\) is the center of the ellipse.
- The line through the foci is the focal axis.
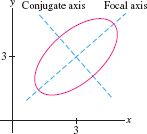
- The line through the center perpendicular to the focal axis is the conjugate axis.
The ellipse is said to be in standard position if the focal and conjugate axes are the \(x\)- and \(y\)-axes, as shown in Figure 11.62. In this case, the foci have coordinates \(F_1 = (c,0)\) and \(F_2=(-c,0)\) for some \(c > 0\). Let us prove that the equation of this ellipse has the particularly simple form \begin{equation} \left(\frac{x}a\right)^2 + \left(\frac{x}b\right)^2 = 1 \tag{2} \end{equation} where \(a=K/2\) and \(b=\sqrt{a^2-c^2}\).
By the distance formula, \(P = (x,y)\) lies on the ellipse in Figure 11.62 if \begin{equation} \label{12.conic.elldistance} PF_1+PF_2 = \sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2} = 2a\tag{3} \end{equation} Move the second term on the left over to the right and square both sides: \begin{align*} (x+c)^2+y^2 &= 4a^2 -4a\sqrt{(x-c)^2+y^2} + (x-c)^2+y^2\\ 4a\sqrt{(x-c)^2+y^2} &= 4a^2 + (x-c)^2 -(x+c)^2 = 4a^2-4cx \end{align*}
642
Now divide by 4, square, and simplify: \begin{align} a^2(x^2 - 2cx+c^2+y^2) &= a^4-2a^2cx + c^2x^2\notag\\ (a^2-c^2) x^2 +a^2y^2 &= a^4 -a^2c^2 = a^2(a^2-c^2)\notag\\ \frac{x^2}{a^2} +\frac{y^2}{a^2-c^2} &= 1\tag{4} \end{align}
This is Eq.(2) with \(b^2 = a^2-c^2\) as claimed.
Note
Strictly speaking, it is necessary to show that if \(P=(x,y)\) satisfies Eq. (4), then it also satisfies Eq. (3). When we begin with Eq. (4) and reverse the algebraic steps, the process of taking square roots leads to the relation \[ \sqrt{(x-c)^2+y^2}\pm\sqrt{(x+c)^2+y^2} = \pm 2a \] However, this equation has no solutions unless both signs are positive because \(a \gt c\).
The ellipse intersects the axes in four points \(A\), \(A'\), \(B\), \(B'\) called vertices. Vertices \(A\) and \(A'\) along the focal axis are called the focal vertices. Following common usage, the numbers \(a\) and \(b\) are referred to as the semimajor axis and the semiminor axis (even though they are numbers rather than axes).
THEOREM 1 Ellipse in Standard Position
Let \(a \gt b \gt 0\), and set \(c =\sqrt{a^2-b^2}\). The ellipse \({{PF_1}+{PF_2}=2a}\) with foci \(F_1 = (c,0)\) and \(F_2 = (-c,0)\) has equation \begin{equation} \boxed{\bbox[#fef7e5,5pt]{\left(\frac{x}a\right)^2 + \left(\frac{y}b\right)^2 = 1}}\tag{5} \end{equation}
Furthermore, the ellipse has
- Semimajor axis \(a\), semiminor axis \(b\).
- Focal vertices \((\pm a,0)\), minor vertices \((0,\pm b)\).
If \(b \gt a \gt 0\), then Eq.(5) defines an ellipse with foci \((0,\pm c)\), where \(c=\sqrt{b^2-a^2}\).
EXAMPLE 1
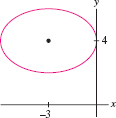
Find the equation of the ellipse with foci \((\pm \sqrt{11},0)\) and semimajor axis \(a=6\). Then find the semiminor axis and sketch the graph.
Solution The foci are \((\pm c, 0)\) with \(c = \sqrt{11}\), and the semimajor axis is \(a=6\), so we can use the relation \(c=\sqrt{a^2-b^2}\) to find \(b\): \[ b^2 = a^2-c^2 = 6^2-(\sqrt{11})^2 = 25\quad\Rightarrow\quad b=5 \]
Thus, the semiminor axis is \(b=5\) and the ellipse has equation \({\left(\frac{x}6\right)^2+\left(\frac{y}5\right)^2=1}\). To sketch this ellipse, plot the vertices \((\pm 6,0)\) and \((0,\pm 5)\) and connect them as in Figure 11.63.
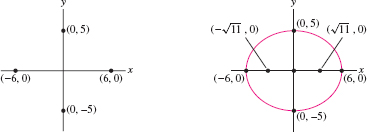
Question 11.141
Find the length of the major axis for the ellipse given by
\( \dfrac{x^2}{9} + \dfrac{y^2}{49} =1\)
| A. |
| B. |
| C. |
| D. |
| E. |
| F. |
643
To write down the equation of an ellipse with axes parallel to the \(x\)- and \(y\)-axes and center translated to the point \(C = (h, k)\), replace \(x\) by \(x-h\) and \(y\) by \(y-k\) in the equation (Figure 11.64): \[ \left(\frac{x-h}a\right)^2+\left(\frac{y-k}b\right)^2=1 \]
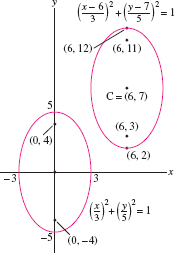
Question 11.142 Section 11.4 Progress Check Question 2
Find the equation of the ellipse with center \((1,-2)\), a focus at \((4,-2)\) and a vertex at \((1,2)\).
| A. |
| B. |
| C. |
| D. |
| E. |
EXAMPLE 2 Translating an Ellipse
Find an equation of the ellipse with center \(C = (6,7)\), vertical focal axis, semimajor axis 5, and semiminor axis 3. Where are the foci located?
Solution Since the focal axis is vertical, we have \(a=3\) and \(b=5\), so that \(a \lt b\) (Figure 11.64). The ellipse centered at the origin would have equation \({\left(\frac{x}3\right)^2+\left(\frac{y}5\right)^2=1}\). When the center is translated to \((h,k) = (6,7)\), the equation becomes \[ \left(\frac{x-6}3\right)^2+\left(\frac{y-7}5\right)^2=1 \]
Furthermore, \(c = \sqrt{b^2-a^2} = \sqrt{5^2-3^2}=4\), so the foci are located \(\pm 4\) vertical units above and below the center—that is, \(F_1 = (6,11)\) and \(F_2 = (6,3)\).
A hyperbola is the set of all points \(P\) such that the difference of the distances from \(P\) to two foci \(F_1\) and \(F_2\) is \(\pm K\): \[ {PF_1}-{PF_2}=\pm K\tag{6} \]
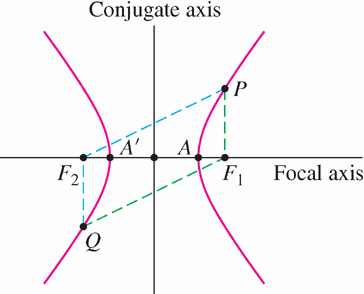
We assume that \(K\) is less than the distance \(F_1F_2\) between the foci (the hyperbola has no points if \(K>F_1F_2\)). Note that a hyperbola consists of two branches corresponding to the choices of sign \(\pm\) (Figure 11.65).
As before, the midpoint of \(\overline{F_1F_2}\) is the center of the hyperbola, the line through \(F_1\) and \(F_2\) is called the focal axis, and the line through the center perpendicular to the focal axis is called the conjugate axis. The vertices are the points where the focal axis intersects the hyperbola; they are labeled \(A\) and \(A'\) in Figure 11.65. The hyperbola is said to be in standard position when the focal and conjugate axes are the \(x\)- and \(y\)-axes as in Figure 11.66. The next theorem can be verified in much the same way as Theorem 1.
THEOREM 2 Hyperbola in Standard Position
Let \(a \gt 0\) and \(b \gt 0\), and set \(c=\sqrt{a^2+b^2}\). The hyperbola \( {PF_1}-{PF_2}=\pm 2a\) with foci \(F_1 = (c,0)\) and \(F_2 = (-c,0)\) has equation \begin{equation} \boxed{\bbox[#fef7e5,5pt]{\left(\frac{x}a\right)^2 - \left(\frac{y}b\right)^2 = 1}}\tag{7} \end{equation}
644
A hyperbola has two asymptotes \({y=\pm\frac{b}ax}\) which are, we claim, diagonals of the rectangle whose sides pass through \((\pm a,0)\) and \((0,\pm b)\) as in Figure 11.66.
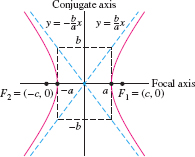
To prove this, consider a point \((x,y)\) on the hyperbola in the first quadrant. By Eq.(7), \[ y = \sqrt{\frac{b^2}{a^2}x^2-b^2} = \frac{b}a\sqrt{x^2-a^2} \]
The following limit shows that a point \((x,y)\) on the hyperbola approaches the line \({y=\frac{b}ax}\) as \(x\to\infty\): \begin{align*} \lim_{x\to\infty}\left(y-\frac{b}ax\right) &=\frac{b}a\lim_{x\to\infty}\left(\sqrt{x^2-a^2}- x\right)\\[-2pt] &=\frac{b}a\lim_{x\to\infty}\left(\sqrt{x^2-a^2}- x\right)\left(\frac{\sqrt{x^2-a^2}+ x}{\sqrt{x^2-a^2}+ x}\right)\\[-2pt] &=\frac{b}a\lim_{x\to\infty} \left(\frac{-a^2}{\sqrt{x^2-a^2}+ x}\right) = 0 \end{align*}
The asymptotic behavior in the remaining quadrants is similar.
EXAMPLE 3
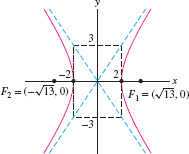
Find the foci of the hyperbola \({9x^2-4y^2= 36}\). Sketch its graph and asymptotes.
Solution First divide by 36 to write the equation in standard form: \[ \frac{x^2}{4}-\frac{y^2}{9}=1\qquad\textrm{or}\qquad \left(\frac{x}{2}\right)^2-\left(\frac{y}3\right)^2 =1 \]
Thus \(a = 2\), \(b = 3\), and \(c = \sqrt{a^2+b^2}=\sqrt{4+9}=\sqrt{13}\). The foci are \[ F_1 = (\sqrt{13},0),\qquad F_2 = (-\sqrt{13},0) \]
To sketch the graph, we draw the rectangle through the points \((\pm 2,0)\) and \((0,\pm 3)\) as in Figure 11.67. The diagonals of the rectangle are the asymptotes \(y=\pm \frac32 x\). The hyperbola passes through the vertices \((\pm 2,0)\) and approaches the asymptotes.
Question 11.143 Section 11.4 Progress Check Question 3
Find the equation of the hyperbola with foci at \((0,6)\) and \((0,-4)\) and a vertex at \((0,5)\).
| A. |
| B. |
| C. |
| D. |
| E. |
Unlike the ellipse and hyperbola, which are defined in terms of two foci, a parabola is the set of points \(P\) equidistant from a focus \(F\) and a line \(\mathcal D\) called the directrix: \begin{equation} {PF} = {P\mathcal D}\tag{8} \end{equation}
Here, when we speak of the distance from a point \(P\) to a line \(\mathcal D\), we mean the distance from \(P\) to the point \(Q\) on \(\mathcal D\) closest to \(P\), obtained by dropping a perpendicular from \(P\) to \(\mathcal D\) (Figure 11.68). We denote this distance by \({P\mathcal D}\).
The line through the focus \(F\) perpendicular to \(\mathcal D\) is called the axis of the parabola. The vertex is the point where the parabola intersects its axis. We say that the parabola is in standard position if, for some \(c\), the focus is \(F = (0,c)\) and the directrix is \(y = -c\), as shown in Figure 11.68. We verify in Exercise 73 that the vertex is then located at the origin and the equation of the parabola is \({y = {x^2}/{4c}}\). If \(c \lt 0\), then the parabola opens downward.
645
THEOREM 3 Parabola in Standard Position
Let \(c\neq 0\). The parabola with focus \(F = (0,c)\) and directrix \(y=-c\) has equation \begin{equation} y = \frac1{4c}x^2\tag{9} \end{equation}
The vertex is located at the origin. The parabola opens upward if \(c \gt 0\) and downward if \(c \lt 0\).
EXAMPLE 4
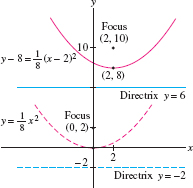
The standard parabola with directrix \(y=-2\) is translated so that its vertex is located at \((2,8)\). Find its equation, directrix, and focus.
Solution By Eq.(9) with \(c=2\), the standard parabola with directrix \(y=-2\) has equation \(y = \frac18x^2\) (Figure 11.69). The focus of this standard parabola is \((0,c)=(0,2)\), which is two units above the vertex \((0,0)\).
To obtain the equation when the parabola is translated with vertex at \((2,8)\), we replace \(x\) by \(x-2\) and \(y\) by \(y-8\): \[ y-8 = \frac18(x-2)^2 \qquad\textrm{or}\qquad y = \frac18x^2 - \frac12x + \frac{17}2 \]
The vertex has moved up \(8\) units, so the directrix also moves up \(8\) units to become \(y = 6\). The new focus is two units above the new vertex \((2,8)\), so the new focus is \((2,10)\).
Question 11.144 Section 11.4 Progress Check Question 4
Find the equation of the directrix of the parabola \(y=x^2\)
| A. |
| B. |
| C. |
| D. |
| E. |
Eccentricity
Some ellipses are flatter than others, just as some hyperbolas are steeper. The “shape” of a conic section is measured by a number \(e\) called the eccentricity. For an ellipse or hyperbola, \[ e = \frac{\textrm{distance betweeen foci}}{\textrm{distance between vertices on focal axis}} \]
A parabola is defined to have eccentricity \(e = 1\).
REMINDER
Standard ellipse: \[ \left(\frac{x}a\right)^2+\left(\frac{y}b\right)^2 = 1,\quad c=\sqrt{a^2-b^2} \]
Standard hyperbola: \[ \left(\frac{x}a\right)^2-\left(\frac{y}b\right)^2 = 1,\quad c=\sqrt{a^2+b^2} \]
THEOREM 4
For ellipses and hyperbolas in standard position, \[e = \frac{c}a\]
- An ellipse has eccentricity \(0\le e \lt 1\).
- A hyperbola has eccentricity \(e \gt 1\).
Proof
The foci are located at \((\pm c,0)\) and the vertices are on the focal axis at \((\pm a,0)\). Therefore, \[ e = \frac{\textrm{distance between foci}}{\textrm{distance between vertices on focal axis}} = \frac{2c}{2a}=\frac{c}a \]
For an ellipse, \(c=\sqrt{a^2-b^2}\) and so \(e = c/a \lt 1\). For a hyperbola, \(c=\sqrt{a^2+b^2}\) and thus \(e=c/a>1\).
646
How does eccentricity determine the shape of a conic [Figure 11.70]? Consider the ratio \(b/a\) of the semiminor axis to the semimajor axis of an ellipse. The ellipse is nearly circular if \(b/a\) is close to \(1\), whereas it is elongated and flat if \(b/a\) is small. Now \[ \frac{b}a = \frac{\sqrt{a^2-c^2}}a = \sqrt{1-\frac{c^2}{a^2}} =\sqrt{1-e^2} \]
This shows that \(b/a\) gets smaller (and the ellipse get flatter) as \(e\to 1\) [Figure 11.70]. The “roundest” ellipse is the circle, with \(e=0\).
Similarly, for a hyperbola, \[\frac{b}{a}=\sqrt{1+e^2}\]
The ratios \(\pm b/a\) are the slopes of the asymptotes, so the asymptotes get steeper as \(e\to\infty\) [Figure 11.70].
Question 11.145 Section 11.4 Progress Check Question 5
Calculate the eccentricity of the conic given by
\( \dfrac{x^2}{4} + y^2 =1\)
| A. |
| B. |
| C. |
| D. |
| E. |
| F. |
CONCEPTUAL INSIGHT
There is a more precise way to explain how eccentricity determines the shape of a conic. We can prove that if two conics \(\mathcal C_1\) and \(\mathcal C_2\) have same eccentricity \(e\), then there is a change of scale that makes \(\mathcal C_1\) congruent to \(\mathcal C_2\). Changing the scale means changing the units along the \(x\)- and \(y\)-axes by a common positive factor. A curve scaled by a factor of \(10\) has the same shape but is ten times as large. This corresponds, for example, to changing units from centimeters to millimeters (smaller units make for a larger figure). By “congruent” we mean that after scaling, it is possible to move \(\mathcal C_1\) by a rigid motion (involving rotation and translation, but no stretching or bending) so that it lies directly on top of \(\mathcal C_2\).
All circles (\(e=0\)) have the same shape because scaling by a factor \(r \gt 0\) transforms a circle of radius \(R\) into a circle of radius \(rR\). Similarly, any two parabolas (\(e=1\)) become congruent after suitable scaling. However, an ellipse of eccentricity \(e=0.5\) cannot be made congruent to an ellipse of eccentricity \(e=0.8\) by scaling (see Exercise 74).
Eccentricity can be used to give a unified focus-directrix definition of the conic sections. Given a point \(F\) (the focus), a line \(\mathcal D\) (the directrix), and a number \(e \gt 0\), we consider the set of all points \(P\) such that \begin{equation} \boxed{\bbox[#fef7e5,5pt]{PF = eP\mathcal D}}\tag{10} \end{equation}
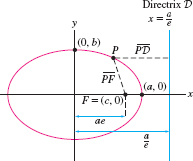
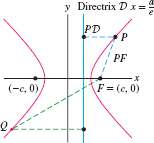
For \(e=1\), this is our definition of a parabola. According to the next theorem, Eq.(10) defines a conic section of eccentricity \(e\) for all \(e \gt 0\) (Figure 11.71 and Figure 11.72). Note, however, that there is no focus-directrix definition for circles (\(e=0\)).
647
THEOREM 5 Focus-Directrix Definition
For all \(e \gt 0\), the set of points satisfying Eq.(10) is a conic section of eccentricity \(e\). Furthermore,
- Ellipse: Let \(a \gt b \gt 0\) and \(c=\sqrt{a^2-b^2}\). The ellipse \[ \left(\frac{x}a\right)^2 + \left(\frac{y}b\right)^2 = 1 \] satisfies Eq.(10) with \(F=(c,0)\), \({e=\frac{c}a}\), and vertical directrix \({x=\frac{a}e}\).
- Hyperbola: Let \(a, b \gt 0\) and \(c=\sqrt{a^2+b^2}\). The hyperbola \[ \left(\frac{x}a\right)^2 - \left(\frac{y}b\right)^2 = 1 \] satisfies Eq.(10) with \(F=(c,0)\), \({e=\frac{c}a}\), and vertical directrix \({x=\frac{a}e}\).
Proof
Assume that \(e \gt 1\) (the case \(e \lt 1\) is similar, see Exercise 66). We may choose our coordinate axes so that the focus \(F\) lies on the \(x\)-axis and the directrix is vertical, lying to the left of \(F\), as in Figure 11.73.
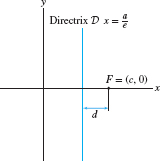
Anticipating the final result, we let \(d\) be the distance from the focus \(F\) to the directrix \(\mathcal D\) and set \[ c =\frac{d}{1-e^{-2}},\qquad a = \frac{c}e,\qquad b = \sqrt{c^2-a^2} \]
Since we are free to shift the \(y\)-axis, let us choose the \(y\)-axis so that the focus has coordinates \(F=(c,0)\). Then the directrix is the line \begin{align*} x &= c-d = c-c(1-e^{-2})\\ &=c\,e^{-2}=\frac{a}e \end{align*}
Now, the equation \({PF = eP\mathcal D}\) for a point \(P=(x,y)\) may be written
\[ \underbrace{\sqrt{(x-c)^2+y^2}}_{PF} = \underbrace{e\sqrt{\bigl(x-(a/e)\bigr)^2}}_{P\mathcal D} \]
Algebraic manipulation yields \(\require{cancel} \)\begin{array}{ccc} (x-c)^2+y^2 &=& e^2\bigl(x-(a/e)\bigr)^2&&&\textrm{(square)}\\ x^2-2cx+c^2 + y^2 &=& e^2x^2-2aex + a^2&&& \\ x^2-\cancel{2aex}+a^2e^2 + y^2 &=& e^2x^2-\cancel{2aex} + a^2&&& \textrm{(use \(c = ae\))}\\ (e^2-1)x^2- y^2 &=& a^2(e^2-1)&&&\textrm{(rearrange)}\\ \frac{x^2}{a^2}-\frac{y^2}{a^2(e^2-1)} &=&1 &&&\textrm{(divide)} \end{array}
This is the desired equation because \({a^2(e^2-1)=c^2-a^2=b^2}\).
648
EXAMPLE 5
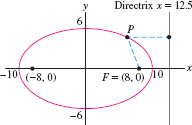
Find the equation, foci, and directrix of the standard ellipse with eccentricity \(e=0.8\) and focal vertices \((\pm 10,0)\).
Solution The vertices are \((\pm a,0)\) with \(a = 10\) (Figure 11.74). By Theorem 5, \( c=ae=10(0.8)=8,\qquad\quad b=\sqrt{a^2-c^2} = \sqrt{10^2-8^2}=6 \)
Thus, our ellipse has equation \[ \left(\frac{x}{10}\right)^2+\left(\frac{y}{6}\right)^2 = 1 \]
The foci are \((\pm c, 0) = (\pm 8,0)\) and the directrix is \({x=\frac{a}e=\frac{10}{0.8}=12.5}\).
In Section 13.8, we discuss the famous law of Johannes Kepler stating that the orbit of a planet around the sun is an ellipse with one focus at the sun. In this discussion, we will need to write the equation of an ellipse in polar coordinates. To derive the polar equations of the conic sections, it is convenient to use the focus-directrix definition with focus \(F\) at the origin \(O\) and vertical line \(x=d\) as directrix \(\mathcal D\) (Figure 11.75).
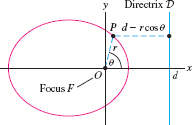
Note from the figure that if \(P=(r,\theta)\), then \[ {PF} = r,\qquad {P\mathcal D} = d - r\cos\theta \]
Thus the focus-directrix equation of the ellipse \({{PF}=e{P\mathcal D}}\) becomes \(r =e(d-r\cos\theta)\), or \(r(1+ e\cos\theta) =ed\). This proves the following result, which is also valid for the hyperbola and parabola (see Exercise 67).
THEOREM 6 Polar Equation of a Conic Section
The conic section of eccentricity \(e \gt 0\) with focus at the origin and directrix \(x=d\) has polar equation \[ \boxed{\bbox[#fef7e5,5pt]{ r =\frac{ed}{1+e\cos\theta}}}\tag{11} \]
EXAMPLE 6
Find the eccentricity, directrix, and focus of the conic section \[ r = \frac{24}{4+3\cos\theta} \]
Solution First, we write the equation in the standard form \[ r = \frac{24}{4+3\cos\theta} = \frac{6}{1+\frac34\cos\theta} \]
Comparing with Eq.(11), we see that \(e=\frac34\) and \(ed=6\). Therefore, \(d=8\). Since \(e \lt 1\), the conic is an ellipse. By Theorem 6, the directrix is the line \(x=8\) and the focus is the origin.
Reflective Properties of Conic Sections
The conic sections have numerous geometric properties. Especially important are the reflective properties, which are used in optics and communications (for example, in antenna and telescope design; Figure 11.76).

We describe these properties here briefly without proof (but see Exercises 68–70 and Exercise 71 for proofs of the reflective property of ellipses).
649
- Ellipse: The segments \(F_1P\) and \(F_2P\) make equal angles with the tangent line at a point \(P\) on the ellipse. Therefore, a beam of light originating at focus \(F_1\) is reflected off the ellipse toward the second focus \(F_2\) [Figure 11.77]. See also Figure 11.78.
- Hyperbola: The tangent line at a point \(P\) on the hyperbola bisects the angle formed by the segments \(F_1P\) and \(F_2P\). Therefore, a beam of light directed toward \(F_2\) is reflected off the hyperbola toward the second focus \(F_1\) [Figure 11.77].
- Parabola: The segment \(FP\) and the line through \(P\) parallel to the axis make equal angles with the tangent line at a point \(P\) on the parabola [Figure 11.77]. Therefore, a beam of light approaching \(P\) from above in the axial direction is reflected off the parabola toward the focus \(F\).

General Equations of Degree 2
The equations of the standard conic sections are special cases of the general equation of degree 2 in \(x\) and \(y\): \begin{equation} \boxed{\bbox[#fef7e5,5pt]{ax^2+bxy+cy^2 + dx+ey+f = 0}}\tag{12} \end{equation}
Here \(a\), \(b\), \(e\), \(d\), \(e\), \(f\) are constants with \(a\), \(b\), \(c\) not all zero. It turns out that this general equation of degree 2 does not give rise to any new types of curves. Apart from certain “degenerate cases,” Eq.(12) defines a conic section that is not necessarily in standard position: It need not be centered at the origin, and its focal and conjugate axes may be rotated relative to the coordinate axes. For example, the equation \[ 6x^2-8xy+8y^2-12x-24y+38=0 \] defines an ellipse with center at \((3,3)\) whose axes are rotated (Figure 11.79).
We say that Eq.(12) is degenerate if the set of solutions is a pair of intersecting lines, a pair of parallel lines, a single line, a point, or the empty set. For example:
- \(x^2-y^2= 0\) defines a pair of intersecting lines \(y=x\) and \(y=-x\).
- \(x^2-x= 0\) defines a pair of parallel lines \(x=0\) and \(x=1\).
- \(x^2 =0\) defines a single line (the \(y\)-axis).
- \(x^2+y^2= 0\) has just one solution \((0,0)\).
- \(x^2+y^2=-1\) has no solutions.
Now assume that Eq.(12) is nondegenerate. The term \(bxy\) is called the cross term. When the cross term is zero (that is, when \(b=0\)), we can “complete the square” to show that Eq.(12) defines a translate of the conic in standard position. In other words, the axes of the conic are parallel to the coordinate axes. This is illustrated in the next example.
EXAMPLE 7 Completing the Square
Show that \[4x^2+9y^2+24x-72y+144=0\] defines a translate of a conic section in standard position (Figure 11.80).
650
Solution Since there is no cross term, we may complete the square of the terms involving \(x\) and \(y\) separately: \begin{align*} 4x^2+9y^2+24x-72y+144 &=0\\ 4(x^2+6x+9-9)+9(y^2-8y+16-16)+144 &= 0\\ 4(x+3)^2 -4(9)+9(y-4)^2-9(16) +144 &= 0\\ 4(x+3)^2 + 9(y-4)^2& = 36 \end{align*}
Therefore, this quadratic equation can be rewritten in the form \[ \left(\frac{x+3}{3}\right)^2 +\left(\frac{y-4}{2}\right)^2 = 1 \]
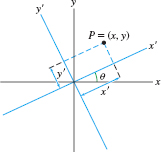
Note
If \((x',y')\) are coordinates relative to axes rotated by an angle \(\theta\) as in Figure 11.81, then \begin{align} x&=x'\cos\theta-y'\sin\theta\tag{13}\\ y&=x'\sin\theta+y'\cos\theta\tag{14} \end{align} See Exercise 75. In Exercise 76, we show that the cross term disappears when Eq.(12) is rewritten in terms of \(x'\) and \(y'\) for the angle \begin{equation} \theta=\frac12\cot^{-1}\frac{a-c}{b}\tag{15} \end{equation}
When the cross term \(bxy\) is nonzero, Eq.(12) defines a conic whose axes are rotated relative to the coordinate axes.
The marginal note describes how this may be verified in general. We illustrate with the following example.
EXAMPLE 8
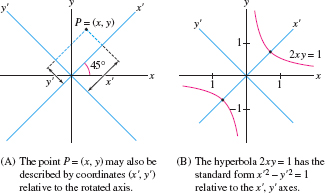
Show that \(2x y = 1\) defines a conic section whose focal and conjugate axes are rotated relative to the coordinate axes.
Solution Figure 11.82 shows axes labeled \(x'\) and \(y'\) that are rotated by \(45^\circ\) relative to the standard coordinate axes. A point \(P\) with coordinates \((x,y)\) may also be described by coordinates \((x', y')\) relative to these rotated axes. Applying Eqs. (13) and (14) with \(\theta=\frac{\pi}4\), we find that \((x,y)\) and \((x',y')\) are related by the formulas \[ x = \frac{x' -y'}{\sqrt{2}}, \qquad y =\frac{x' +y'}{\sqrt{2}} \]
Therefore, if \(P=(x,y)\) lies on the hyperbola—that is, if \(2xy=1\)—then \[ 2x y = 2 \left( \frac{x' -y'}{\sqrt{2}}\right) \left( \frac{x' + y'}{\sqrt{2}}\right) = x^{\prime2}-y^{\prime2} =1 \]
Thus, the coordinates \((x',y')\) satisfy the equation of the standard hyperbola \(x^{\prime2}-y^{\prime2} =1\) whose focal and conjugate axes are the \(x'\)- and \(y'\)-axes, respectively.
We conclude our discussion of conics by stating the Discriminant Test. Suppose that the equation \[ ax^2+bxy+cy^2 + dx+ey+f = 0 \]
651
is nondegenerate and thus defines a conic section. According to the Discriminant Test, the type of conic is determined by the discriminant \(D\): \[\boxed{\bbox[#fef7e5,5pt]{D = b^2-4ac}} \]
We have the following cases:
- \(D \lt 0\): Ellipse or circle
- \(D \gt 0\): Hyperbola
- \(D=0\): Parabola
For example, the discriminant of the equation \(2xy=1\) is \[ D = b^2-4ac=2^2-0 = 4 >0 \]
According to the Discriminant Test, \(2xy=1\) defines a hyperbola. This agrees with our conclusion in Example 8.
Question 11.146 Section 11.4 Progress Check Question 6
The following equation of degree 2 represents a conic section. What kind?
\(2x^2 + 3xy +y^2-5y-2=0\)
| A. |
| B. |
| C. |
| D. |
| E. |
Summary
An ellipse with foci \(F_1\) and \(F_2\) is the set of points \(P\) such that \({{PF_1} + {PF_2} = K}\), where \(K\) is a constant such that \(K \gt F_1F_2\). The equation in standard position is \[ \left(\frac{x}a\right)^2+\left(\frac{y}b\right)^2=1 \]
The vertices of the ellipse are \((\pm a, 0)\) and \((0, \pm b)\).
Focal axis Foci Focal vertices \(a \gt b\) \(x\)-axis \((\pm c, 0)\) with \(c=\sqrt{a^2-b^2}\) \((\pm a,0)\) \(a \lt b\) \(y\)-axis \((0,\pm c)\) with \(c=\sqrt{b^2-a^2}\) \((0,\pm b)\) Eccentricity: \({e=\tfrac{c}a}\) \((0\le e \lt 1)\). Directrix: \({x=\tfrac{a}e}\) (if \(a \gt b\)).
A hyperbola with foci \(F_1\) and \(F_2\) is the set of points \(P\) such that \[ {PF_1} - {PF_2} = \pm K \]
where \(K\) is a constant such that \(0 \lt K \lt F_1F_2\). The equation in standard position is \[ \left(\frac{x}a\right)^2-\left(\frac{y}b\right)^2=1 \]
Focal axis Foci Vertices Asymptotes \(x\)-axis \((\pm c,0)\) with \(c=\sqrt{a^2+b^2}\) \((\pm a,0)\) \(y=\pm\dfrac{b}{a}x\) Eccentricity: \({e=\tfrac{c}a}\) \((e \gt 1)\). Directrix: \({x=\tfrac{a}e}\).
A parabola with focus \(F\) and directrix \(\mathcal D\) is the set of points \(P\) such that \({{PF}={P\mathcal D}}\). The equation in standard position is \[ y=\frac1{4c}x^2 \]
Focus \(F=(0,c)\), directrix \(y = - c\), and vertex at the origin \((0,0)\).
652
- Focus-directrix definition of conic with focus \(F\) and directrix \(\mathcal D\): \(PF = eP\mathcal D\).
- To translate a conic section \(h\) units horizontally and \(k\) units vertically, replace \(x\) by \(x-h\) and \(y\) by \(y-k\) in the equation.
- Polar equation of conic of eccentricity \(e \gt 0\), focus at the origin, directrix \(x = d\): \[ r = \frac{ed}{1 + e\cos\theta} \]