11.5 Polar, Cylindrical and Spherical Coordinates
52
Polar coordinates
A standard way to represent a point in the plane \({\mathbb R}^2\) is by means of rectangular coordinates \((x,y)\). However, as you have probably learned in elementary calculus, polar coordinates in the plane can be extremely useful. Polar coordinates are appropriate when distance from the origin or angle plays a role. For example, the gravitational force exerted on a planet by the sun depends only on the distance \(r\) from the sun and is conveniently described in polar coordinates.
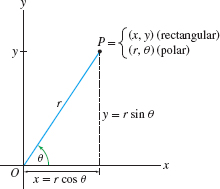
In polar coordinates, we label a point \(P\) by coordinates \((r,\theta)\), where \(r\) is the distance to the origin \(O\) and \(\theta\) is the angle between \(\overline{OP}\) and the positive \(x\)-axis (Figure 11.83). By convention, an angle is positive if the corresponding rotation is counterclockwise. We call \(r\) the radial coordinate and \(\theta\) the angular coordinate. As portrayed in Figure 11.83, the coordinates \((r,\theta)\) are related to \((x,y)\) by the formulas \[ x = r \cos \theta \qquad \hbox{and} \qquad y = r \sin \theta, \] where we usually take \(r \ge 0\) and \(0 \le \theta < 2 \pi\).
The point \(P\) in Figure 11.84 has polar coordinates \((r, \theta) =\big(4,\frac{2\pi}3\big)\). It is located at distance \(r= 4\) from the origin (so it lies on the circle of radius 4), and it lies on the ray of angle \(\theta=\frac{2\pi}{3}\).
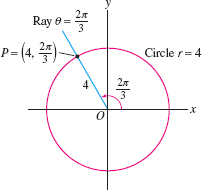
Figure 11.85 shows the two families of grid lines in polar coordinates: \[ \begin{array}\\ \hbox{Circle centered at \(O\)} & \longleftrightarrow & r &{}={}& \hbox{constant}\\ \hbox{Ray starting at \(O\)} & \longleftrightarrow &\theta &=& \hbox{constant} \end{array} \]
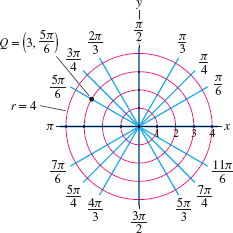
Every point in the plane other than the origin lies at the intersection of the two grid lines and these two grid lines determine its polar coordinates. For example, point \(Q\) in Figure 11.85 lies on the circle \(r=3\) and the ray \(\theta = \frac{5\pi}6\), so \(Q=\big(3,\frac{5\pi}6\big)\) in polar coordinates.
Figure 11.83 shows that polar and rectangular coordinates are related by the equations \(x=r\cos\theta\) and \(y=r\sin \theta\). On the other hand, \(r^2=x^2+y^2\) by the distance formula, and \(\tan\theta={y}/{x}\) if \(x \neq 0\). This yields the conversion formulas:
| Polar to Rectangular | Rectangular to Polar |
| \(x=r\cos\theta\) | \(r=\sqrt{x^2+y^2}\) |
| \(y = r\sin\theta\) | \(\tan\theta=\frac{y}{x}\quad (x\neq 0)\) |
627
Historical Note
In 1671, Isaac Newton wrote a manuscript entitled The Method of Fluxions and Infinite Series, which contains many uses of coordinate geometry to sketch the solutions of equations. In particular, he introduces the polar coordinate system, among various other coordinate systems.
In 1691, Jacob Bernoulli published a paper also containing polar coordinates. Because Newton’s manuscript was not published until after his death in 1727, credit for the discovery of polar coordinates is usually attributed to Bernoulli.
EXAMPLE 1 From Polar to Rectangular Coordinates
Find the rectangular coordinates of point \(Q\) in Figure 11.85.
Solution The point \(Q= (r,\theta) = \big(3,\frac{5\pi}6\big)\) has rectangular coordinates: \begin{align*} x &= r\cos\theta = 3\cos\left(\frac{5\pi}6\right) =3\left(-\frac{\sqrt{3}}2\right) = -\frac{3\sqrt{3}}2\\ y &= r\sin\theta =3\sin\left(\frac{5\pi}6\right) =3\left(\frac{1}2\right) = \frac32 \end{align*}
Question 11.147 Section 11.5 Progress Check Question 1
Find the rectangular coordinates of the point \(P\) with polar coordinates \((4, \dfrac{3 \pi}{4})\).
| A. |
| B. |
| C. |
| D. |
| E. |
EXAMPLE 2 From Rectangular to Polar Coordinates
Find the polar coordinates of point \(P\) in Figure 11.86.
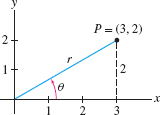
Solution Since \(P=(x,y)=(3,2)\), \begin{align*} r&=\sqrt{x^2+y^2}=\sqrt{3^2+2^2}=\sqrt{13}\approx 3.6\\ \tan\theta &= \frac{y}{x} = \frac23 \end{align*} and because \(P\) lies in the first quadrant, \begin{align*} \theta &= \tan^{-1} \frac{y}x = \tan^{-1} \frac23 \approx 0.588 \end{align*} Thus, \(P\) has polar coordinates \((r,\theta) \approx (3.6,0.588)\).
Definition
By definition, \[ -\frac{\pi}2<\tan^{-1} x < \frac{\pi}2 \] If \(r>0\), a coordinate \(\theta\) of \(P=(x,y)\) is \[ \theta = \begin{cases} \tan^{-1}\frac{y}x & \text{ if \(x > 0\)} \\ \tan^{-1}\frac{y}x +\pi & \text{ if \(x<0\)}\\ \pm \frac{\pi}{2}& \text{ if \(x = 0\)} \end{cases} \]}
Question 11.148 Section 11.5 Progress Check Question 2
Find polar coordinates of the point \(P\) with rectangular coordinates \((\frac{\sqrt{5}}{2}, -\frac{\sqrt{15}}{2})\).
| A. |
| B. |
| C. |
| D. |
| E. |
A few remarks are in order before proceeding:
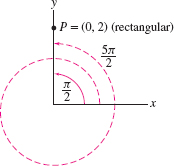
- The angular coordinate is not unique because \((r,\theta)\) and \((r,\theta+2\pi n)\) label the same point for any integer \(n\). For instance, point \(P\) in Figure 11.87 has radial coordinate \(r=2\), but its angular coordinate can be any one of \(\frac{\pi}2\), \(\frac{5\pi}2,\ldots\) or \(-\frac{3\pi}2\), \(-\frac{7\pi}2, \ldots.\)
- The origin \(O\) has no well-defined angular coordinate, so we assign to \(O\) the polar coordinates \((0,\theta)\) for any angle \(\theta\).
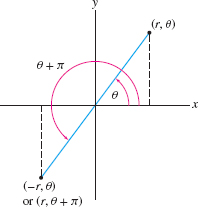
- By convention, we allow negative radial coordinates. By definition, \((-r,\theta)\) is the reflection of \((r,\theta)\) through the origin (Figure 11.88). With this convention, \((-r,\theta)\) and \((r,\theta+\pi)\) represent the same point.
- We may specify unique polar coordinates for points other than the origin by placing restrictions on \(r\) and \(\theta\). We commonly choose \(r>0\) and \(0\le \theta < 2\pi\).
628
When determining the angular coordinate of a point \(P=(x,y)\), remember that there are two angles between \(0\) and \(2\pi\) satisfying \(\tan\theta= {y}/x\). You must choose \(r\) and \(\theta\) so that \((r,\theta)\) lies in the quadrant containing \(P\) and not in the opposite quadrant (Figure 11.89).
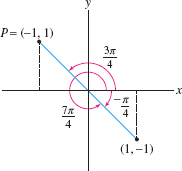
EXAMPLE 3 Choosing \(\theta\) Correctly
Find two polar representations of \(P = (-1,1)\), one with \(r>0\) and one with \(r<0\).
Solution The point \(P=(x,y) = (-1,1)\) has polar coordinates \((r,\theta)\), where \[ r=\sqrt{(-1)^2+1^2}=\sqrt 2,\qquad \tan\theta=\tan\frac{y}{x}=-1 \] However, \(\theta\) is not given by \[ \tan^{-1}\frac{y}x = \tan^{-1}\left(\frac1{-1}\right) = -\frac{\pi}4 \] because \(\theta = -\frac{\pi}4\) this would place \(P\) in the fourth quadrant (Figure 11.89). Since \(P\) is in the second quadrant, the correct angle is \[ \theta =\tan^{-1}\frac{y}x +\pi = -\frac{\pi}4 + \pi = \frac{3\pi}4 \] If we wish to use the negative radial coordinate \(r= -\sqrt 2\), then the angle becomes \(\theta= -\frac{\pi}4\) or \(\frac{7\pi}4\). Thus, \[ P = \left(\sqrt 2,\frac{3\pi}4\right)\qquad \textrm{or} \qquad \left(-\sqrt 2,\frac{7\pi}4\right) \]
A curve is described in polar coordinates by an equation involving \(r\) and \(\theta\), which we call a polar equation. By convention, we allow solutions with \(r<0\).
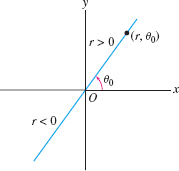
A line through the origin \(O\) has the simple equation \(\theta=\theta_0\), where \(\theta_0\) is the angle between the line and the \(x\)-axis (Figure 11.90). Indeed, the points with \(\theta=\theta_0\) are \((r,\theta_0)\), where \(r\) is arbitrary (positive, negative, or zero).
EXAMPLE 4 Line Through the Origin
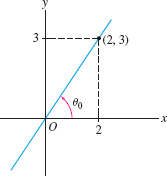
Find the polar equation of the line through the origin of slope \(\frac32\) (Figure 11.91).
Solution A line of slope \(m\) makes an angle \(\theta_0\) with the \(x\)-axis, where \(m=\tan\theta_0\). In our case, \(\theta_0 = \tan^{-1}\frac32 \approx 0.98\). The equation of the line is \(\theta= \tan^{-1} \frac32\) or \(\theta \approx 0.98\).
To describe lines that do not pass through the origin, we note that any such line has a unique point \(P_0\) that is closest to the origin. The next example shows how to write down the polar equation of the line in terms of \(P_0\) (Figure 11.92).
629
EXAMPLE 5 Line Not Passing Through \(O\)
Show that \begin{equation} \boxed{\bbox[#fef7e5,5pt]{r=d\sec(\theta-\alpha)}}\tag{1} \end{equation} is the polar equation of the line \(L\) whose point closest to the origin is \(P_0 = (d,\alpha)\).
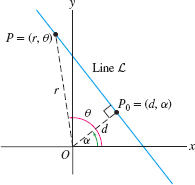
Solution The point \(P_0\) is obtained by dropping a perpendicular from the origin to \(L\) (Figure 11.92), and if \(P = (r,\theta)\) is any point on \(L\) other than \(P_0\), then \(\triangle \textit{OPP}_0\) is a right triangle. Therefore, \({d}/{r} = \cos(\theta - \alpha)\), or \(r = d\sec(\theta - \alpha)\), as claimed.
EXAMPLE 6
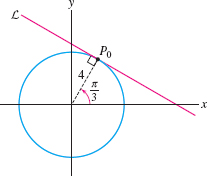
Find the polar equation of the line \(L\) tangent to the circle \(r=4\) at the point with polar coordinates \(P_0=\big(4,\frac{\pi}3\big)\).
Solution The point on \(L\) closest to the origin is \(P_0\) itself (Figure 11.93). Therefore, we take \((d,\alpha)=\big(4,\frac{\pi}3\big)\) in Eq. (1) to obtain the equation \(r=4\sec\big(\theta-\frac{\pi}3\big)\).
Often, it is hard to guess the shape of a graph of a polar equation. In some cases, it is helpful rewrite the equation in rectangular coordinates.
EXAMPLE 7 Converting to Rectangular Coordinates
Identify the curve with polar equation \(r=2a\cos\theta\) (\(a\) a constant).
Solution Multiply the equation by \(r\) to obtain \(r^2=2ar\cos\theta\). Because \(r^2=x^2+y^2\) and \(x=r\cos\theta\), this equation becomes \[ x^2+y^2 = 2ax\qquad\textrm{or}\qquad x^2-2ax+y^2= 0 \] Then complete the square to obtain \((x-a)^2+y^2=a^2\). This is the equation of the circle of radius \(a\) and center \((a,0)\) (Figure 11.94).
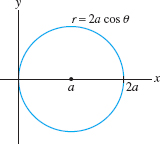
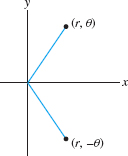
A similar calculation shows that the circle \(x^2 + (y-a)^2 = a^2\) of radius \(a\) and center \((0,a)\) has polar equation \(r=2a\sin\theta\). In the next example, we make use of symmetry. Note that the points \((r,\theta)\) and \((r,-\theta)\) are symmetric with respect to the \(x\)-axis (Figure 11.95).
EXAMPLE 8 Symmetry About the \(x\)-Axis
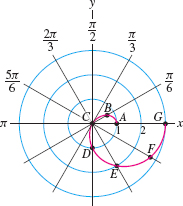
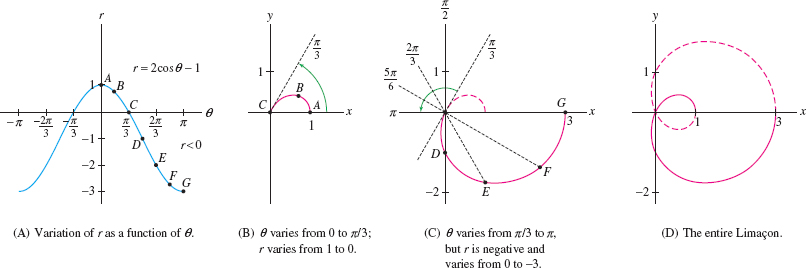
Sketch the limaçon curve \newline \(r = 2\cos\theta-1\).
Solution Since \(\cos\theta\) is periodic, it suffices to plot points for \(-\pi\le \theta\le \pi\).
Step 1. Plot points
To get started, we plot points \(A\)–\(G\) on a grid and join them by a smooth curve (Figure 11.96).
630
| \(A\) | \(B\) | \(C\) | \(D\) | \(E\) | \(F\) | \(G\) | |
| \(\theta\) | 0 | \(\frac{\pi}6\) | \(\frac{\pi}3\) | \(\frac{\pi}2\) | \(\frac{2\pi}3\) | \(\frac{5\pi}6\) | \(\pi\) |
| \(r= 2 \cos \theta -1\) | 1 | 0.73 | 0 | \(-1\) | \(-2\) | \(-2.73\) | \(-3\) |
Step 2. Analyze \(r\) as a function of \(\theta\)
For a better understanding, it is helpful to graph \(r\) as a function of \(\theta\) in rectangular coordinates. Figure 11.97 shows that
| As \(\theta\) varies from 0 to \(\frac{\pi}3\), | \(r\) varies from 1 to 0. |
| As \(\theta\) varies from \(\frac{\pi}3\) to \(\pi\), | \(r\) is negative and varies from 0 to \(-3\). |
We conclude:
- The graph begins at point \(A\) in Figure 11.97(A) and moves in toward the origin as \(\theta\) varies from \(0\) to \(\frac{\pi}3\).
- Since \(r\) is negative for \(\frac{\pi}3\le\theta\le \pi\), the curve continues into the third and fourth quadrants (rather than into the first and second quadrants), moving toward the point \(G = (-3,\pi)\) in Figure 11.97(C).
Step 3. Use symmetry
Since \(r(\theta)=r(-\theta)\), the curve is symmetric with respect to the \(x\)-axis. So the part of the curve with \(-\pi\le\theta\le 0\) is obtained by reflection through the \(x\)-axis as in Figure 11.97(D).
We now set forth two ways of representing points in space other than by using rectangular Cartesian coordinates \((x,y,z)\). These alternative coordinate systems are particularly well suited for certain types of problems, such as the evaluation of integrals using a change of variables.
Cylindrical Coordinates
Definition
The cylindrical coordinates \((r,\theta,z)\) of a point \((x,y,z)\) are defined by (see Figure 11.98) \begin{equation} x = r \cos \theta, y = r \sin \theta, z=z. \end{equation}
53
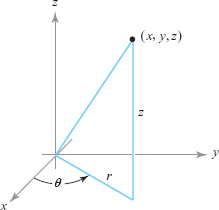
To express \(r,\theta\), and \(z\) in terms of \(x,y\), and \(z\), and to ensure that \(\theta\) lies between \(0\) and \(2\pi\), we can write \[ r=\textstyle\sqrt{x^2+y^2\ }, \hskip17.8pt \theta=\left\{ \begin{array}{@{}l@{\qquad}l@{\qquad}l@{}} \tan^{-1}(\kern1pty/x) & \hbox{if } x>0 \hbox{ and } y\geq 0\\[2pt] \pi + \tan^{-1}(\kern1pty/x)& \hbox{if } x < 0\\[2pt] 2\pi+\tan^{-1}(\kern1pty/x) & \hbox{if }x> 0 \hbox{ and }y<0, \end{array} \right. \hskip-4ptz=z, \] where \(\tan^{-1}(\hskip1pty/x)\) is taken to lie between \(-\pi/2\) and \(\pi/2\). The requirement that \(0 \le \theta < 2\pi\) uniquely determines \(\theta\) and \(r \ge 0\) for a given \(x\) and \(y\). If \(x=0\), then \(\theta=\pi/2\) for \(y>0\) and \(3\pi /2\) for \(y<0\). If \(x=y=0,\theta\) is undefined.
In other words, for any point \((x,y,z)\), we represent the first and second coordinates in terms of polar coordinates and leave the third coordinate unchanged. Formula (1) shows that, given \((r, \theta,z)\), the triple \((x,y,z)\) is completely determined, and vice versa, if we restrict \(\theta\) to the interval \([0,2 \pi)\) (sometimes the range \(( - \pi , \pi]\) is convenient) and require that \(r > 0\).
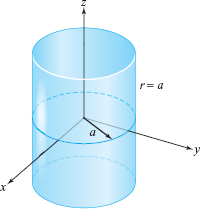
To see why we use the term cylindrical coordinates, note that if the conditions \(0 \le \theta \,{<}\,2\pi, - \infty < z < \infty\) hold and if \(r=a\) is some positive constant, then the locus of these points is a cylinder of radius \(a\) (see Figure 11.99).
example 1
(a) Find and plot the cylindrical coordinates of (6, 6, 8). (b) If a point has cylindrical coordinates \((8,2 \pi/3, -3)\), what are its Cartesian coordinates\(?\) Plot.
solution For part (a), we have \(r = \sqrt{6^2 + 6^2} = 6 \sqrt{2}\) and \(\theta = \tan^{-1} (6/6)= \tan^{-1} (1) = \pi/4\). Thus, the cylindrical coordinates are \((6\sqrt{2}, \pi /4, 8)\). This is point P in Figure 11.100.
54
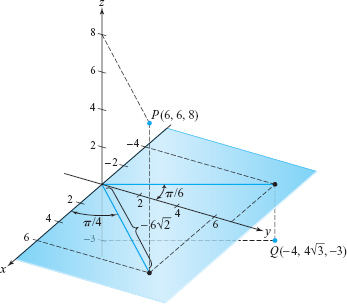
For part (b), note that \(2\pi/3 =\pi/2 + \pi/6\) and compute \[ x = r \cos \theta = 8 \cos \frac{2 \pi}{3} = - \frac{8}{2} =-4 \] and \[ y =r \sin \theta = 8 \sin \frac{2 \pi}{3} = 8 \frac{ \sqrt{3}}{2} = 4 \sqrt{3}. \]
Thus, the Cartesian coordinates are \((-4,4 \sqrt{3},-3)\). This is point Q in the figure.
Question 11.149 Section 11.5 Progress Check Question 3
If a point has cylindrical coordinates \((2, \dfrac{3 \pi}{4}, 2)\), what are its Cartesian coordinates?
| A. |
| B. |
| C. |
| D. |
| E. |
Spherical Coordinates
Cylindrical coordinates are not the only possible generalization of polar coordinates to three dimensions. Recall that in two dimensions the magnitude of the vector \(x {\bf i}+ y {\bf j}\) \(\big(\)that is, \(\sqrt{x^2 + y^2}\big)\) is the \(r\) in the polar coordinate system. For cylindrical coordinates, the length of the vector \(x {\bf i} + y {\bf j} + z {\bf k}\), namely, \[ \rho=\textstyle \sqrt{x^2 + y^2 + z^2}, \] is not one of the coordinates of that system—instead, we used the magnitude \(r = \sqrt{x^2 + y^2}\), the angle \(\theta\), and the “height” \(z\).
We now modify this by introducing the spherical coordinate system, which does use \(\rho\) as a coordinate. Spherical coordinates are often useful for problems that possess spherical symmetry (symmetry about a point), whereas cylindrical coordinates can be applied when cylindrical symmetry (symmetry about a line) is involved.
55
Given a point \(P(x,y,z) \in {\mathbb R}^3\), let \[ \rho = \textstyle\sqrt{x^2 + y^2 + z^2} \] and represent \(x\) and \(y\) by polar coordinates in the \(xy\) plane: \begin{equation} x = r \cos \theta, y= r \sin \theta,\tag{2} \end{equation} where \(r = \sqrt{x^2 + y^2}\) and \(\theta\) is determined by formula (1) [see the expression for \(\theta\) following formula (1)].
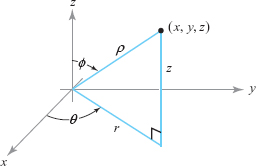

The coordinate \(z\) is given by \[ z = \rho \cos \phi, \]
where \(\phi\) is the angle (chosen to lie between 0 and \(\pi\), inclusive) that the radius vector \({\bf v} = x {\bf i} + y {\bf j} + z {\bf k}\) makes with the positive \(z\) axis, in the plane containing the vector \({\bf v}\) and the \(z\) axis (see Figure 11.101). Using the dot product, we can express \(\phi\) as follows: \[ \cos \phi = \frac{{\bf v \,{\cdot}\, k}}{\|{\bf v}\|}, \hbox{that is}, \phi = \cos^{-1} \!\bigg( \frac{{\bf v \,{\cdot}\, k}}{\|{\bf v}\|} \bigg). \]
We take as our coordinates the quantities \(\rho,\theta,\phi\). Because \[ r=\rho\sin \phi, \] we can use formula (2) to find \(x,y,z\) in terms of the spherical coordinates \(\rho,\theta,\phi\).
Definition
The spherical coordinates of points \((x, y, z)\) in space are the triples \((\rho, \theta, \phi)\), defined as follows: \begin{equation} x=\rho\sin \phi \cos \theta, y=\rho\sin\phi\sin\theta, z=\rho\cos \phi,\tag{3} \end{equation} where \[ \rho\geq 0, 0\,\leq\, \theta\,<\,2\pi, 0\leq \phi\leq \pi. \]
56
Historical Note
In 1773, Joseph Louis Lagrange was working on Newton’s gravitational theory as it applied to ellipsoids of revolution. In attempting to calculate the total gravitational attraction of such an ellipsoid, he encountered an integral that was difficult to evaluate. Motivated by this application, he introduced spherical coordinates, which allowed him to calculate the integral. We will be discussing the method of changing coordinates as it applies to multiple integrals in Section 16.2, and applications to gravitation in Section 16.3, where we show how the inverse square law of gravity allowed Newton to consider spherical masses as point masses.
Spherical coordinates are also closely connected to navigation by latitude and longitude. To see the connection, first note that the sphere of radius \(a\) centered at the origin is described by a very simple equation in spherical coordinates, namely, \(\rho = a\;\). Fixing the radius \(a\), the spherical coordinates \(\theta \) and \(\phi \) are similar to the geographic coordinates of longitude and latitude if we take the earth’s axis to be the \(z\) axis. There are differences, though: The geographical longitude is \(\vert \theta \vert \) and is called east or west longitude, according to whether \(\theta \) is a positive or negative measure from the Greenwich meridian; the geographical latitude is \(\vert \pi/2\,{-}\, \phi \vert\) and is called north or south latitude, according to whether \(\pi/2\,{-}\,\phi\) is positive or negative.
example 2
- (a) Find the spherical coordinates of the Cartesian point \((1,-1,1)\) and plot.
- (b) Find the Cartesian coordinates of the spherical coordinate point \((3, \pi /6, \pi /4)\) and plot.
- (c) Let a point have Cartesian coordinates \((2,-3, 6)\). Find its spherical coordinates and plot.
- (d) Let a point have spherical coordinates \((1, -\pi /2, \pi /4)\). Find its Cartesian coordinates and plot.
solution
- (a) \(\rho = \sqrt{x^2 + y^2 + z^2} = \sqrt{1^2 + (-1)^2 + 1^2} = \sqrt{3}\),
- \(\theta = 2\pi +\tan^{-1} \!\left( \displaystyle\frac{y}{x} \right) = 2\pi +\tan^{-1}\! \left( \displaystyle\frac{-1}{1} \right) = 2\pi- \displaystyle\frac{\pi}{4}=\frac{7\pi}{4}\)
- \(\phi= \cos^{-1} \!\left( \displaystyle\frac{z}{\rho} \right) = \cos^{-1}\! \left( \displaystyle\frac{1}{\sqrt{3}} \right) \approx 0.955 \approx 54.74^\circ.\)
- (b) \(x = \rho \sin \phi \cos \theta = 3 \sin \!\left( \displaystyle\frac{\pi}{4} \right) \cos \!\left(\displaystyle \frac{\pi}{6} \right) =3\! \left(\displaystyle \frac{1}{\sqrt{2}} \right) \displaystyle\frac{\sqrt{3}}{2} = \displaystyle\frac{3 \sqrt{3}}{2 \sqrt{2}}\),
- \(y = \rho \sin \phi \sin \theta = 3 \sin \! \Big(\displaystyle\frac{\pi}{4}\Big) \sin \!\left(\displaystyle\frac{\pi}{6}\right) = 3\! \left(\frac{1}{\sqrt{2}}\right)\! \left(\displaystyle\frac{1}{2} \right) = \displaystyle \frac{3}{2 \sqrt{2}}\),
- \(z= \rho \cos \phi = 3 \cos\! \Big(\displaystyle\frac{\pi}{4}\Big) = \displaystyle\frac{3}{\sqrt{2}} = \displaystyle\frac{3\sqrt{2}}{2} .\)
See Figure 11.103.
57
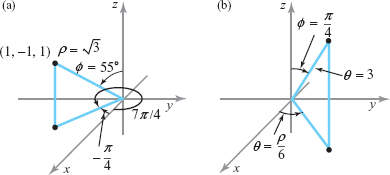 Figure 11.103: Finding (a) the spherical coordinates of the point (1, –1, 1), and (b) the Cartesian coordinates of (3, \(\pi/6\), \(\pi/4\)).
Figure 11.103: Finding (a) the spherical coordinates of the point (1, –1, 1), and (b) the Cartesian coordinates of (3, \(\pi/6\), \(\pi/4\)). - (c) \(\rho = \sqrt{ x^2 + y^2 + z^2} = \sqrt{ 2^2 + (-3)^2 + 6^2} = \sqrt{49} = 7\),
- \(\theta = 2\pi+\tan^{-1} \!\left(\displaystyle\frac{y}{x}\right) =2\pi+ \tan^{-1} \! \left(\displaystyle\frac{-3}{2}\right) \approx 5.3004 \hbox{ radians} \approx 303.69^\circ,\)
- \(\phi = \cos^{-1} \! \left(\displaystyle\frac{z}{\rho} \right) = \cos^{-1}\! \left(\displaystyle\frac{6}{7} \right) \approx 0.541 \approx 31.0^\circ.\)
- (d) \(x= \rho \sin \phi \cos \theta = 1 \sin\! \left(\displaystyle\frac{\pi}{4} \right) \cos \! \left(\displaystyle -\frac{\pi}{2} \right) = \bigg(\displaystyle\frac{\sqrt{2}}{2} \bigg) \,{\cdot} \ 0 =0,\)
- \(y = \rho \sin \phi \sin \theta = 1 \sin \! \left(\displaystyle\frac{\pi}{4} \right) \sin \!\left(\displaystyle -\frac{ \pi}{2} \right)= \bigg(\displaystyle\frac{\sqrt{2}}{2} \bigg) (-1) = -\frac{\sqrt{2}}{2}\),
- \(z = \rho \cos \phi = 1\cos \! \Big(\displaystyle\frac{\pi}{4} \Big) = \displaystyle\frac{\sqrt{2}}{2}.\)
 Figure 11.104: Finding (a) the spherical coordinates of the point (2, \(-3\), 6), and (b) the Cartesian coordinates of (1, \(-\pi/2\), \(\pi/4\)).
Figure 11.104: Finding (a) the spherical coordinates of the point (2, \(-3\), 6), and (b) the Cartesian coordinates of (1, \(-\pi/2\), \(\pi/4\)).
58
example 3
Express (a) the surface \(xz=1\) and (b) the surface \(x^2 + y^2 - z^2 \,{=}\,1\) in spherical coordinates.
solution From formula (3), \(x = \rho \sin \phi \cos \theta, \hbox{and } z = \rho \cos \phi\), and so the surface \(xz = 1\) in (a) consists of all \((\rho, \theta, \phi)\) such that \[ \rho^2 \sin \phi \cos \theta \cos \phi =1, \qquad\hskip-2.5pt \hbox{that is,} \qquad \rho^2 \sin 2 \phi \cos \theta =2. \]
For part (b), we can write \[ x^2 + y^2 - z^2 = x^2 + y^2 + z^2 - 2 z^2 = \rho^2- 2 \rho^2 \cos^2 \phi, \] so that the surface is \(\rho^2 (1-2 \cos^2 \phi) =1;\) that is, \(- \rho^2 \cos\, ( 2 \phi) =1\).
Question 11.150 Section 11.5 Progress Check Question 4
Express the surface \(x^2 + 2y^2 +z^2 \,{=}\,1\) in spherical coordinates.
| A. |
| B. |
| C. |
| D. |
| E. |
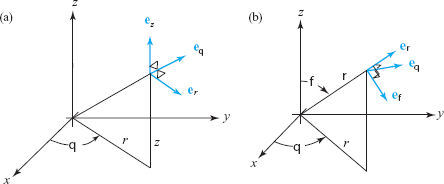
Associated with cylindrical and spherical coordinates are unit vectors that are the counterparts of \({\bf i},{\bf j}\), and \({\bf k}\) for rectangular coordinates. They are shown in Figure 11.105. For example, \({\bf e}_r\) is the unit vector parallel to the \(xy\) plane and in the radial direction, so that \({\bf e}_r =(\cos \theta){\bf i}+(\sin \theta){\bf j}\). Similarly, in spherical coordinates, \({\bf e}_\phi\) is the unit vector tangent to the curve parametrized by the variable \(\phi\) with the variables \(\rho\) and \(\theta\) held fixed. We shall use these unit vectors later when we use cylindrical and spherical coordinates in vector calculations.