12.3 Arc Length
Definition of Arc Length
What is the length of a path \({\bf c}(t)\)? Because the speed \(\|{\bf c}'(t)\|\) is the rate of change of distance traveled with respect to time, the distance traveled by a point moving along the curve should be the integral of speed with respect to the time over the interval \([t_0,t_1]\) of travel time; that is, the length of the path, also called its arc length, is \[ L({\bf c})= \int^{t_1}_{t_0} \|{\bf c}'(t)\|\ {\it dt}. \]
There is the question as to whether or not this formula actually corresponds to the true arc length. For example, suppose we take a curve in space and glue a string tightly to it, cutting the string so it exactly fits the curve. If we then remove the string, straighten it out, and measure it with a straight edge, we surely should obtain the length of the curve.
To see a justification that our formula for arc length agrees with such a process, click here.
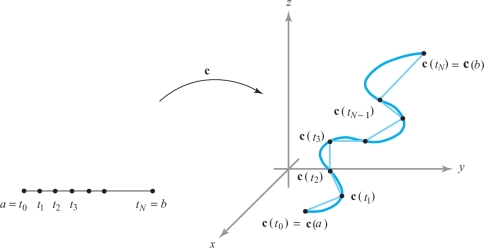
In \({\mathbb R}^3\) there is another way to justify the arc-length formula based on polygonal approximations. We partition the interval \([a,b]\) into \(N\) subintervals of equal length: \begin{eqnarray*} &\displaystyle a = t_0 < t_1 < \cdots < t_N =b; &\\[3pt] &\displaystyle t_{i+1} - t_i = \frac{b-a}{N} \quad {\rm for} \quad 0 \le i \le N-1.& \end{eqnarray*}
We then consider the polygonal line obtained by joining the successive pairs of points \({\bf c} (t_i), {\bf c} (t_{i+1})\) for \(0 \le i \le N-1\). This yields a polygonal approximation to \({\bf c}\) as in Figure 12.19. By the formula for distance in \({\mathbb R}^3\), it follows that the line segment from \({\bf c} (t_i)\) to \({\bf c} ( t_{i+1})\) has length \[ \| {\bf c} (t_{i+1}) - {\bf c} (t_i) \| = \sqrt{[x (t_{i+1}) - x (t_i) ]^2+ [ y ( t_{i+1}) - y (t_i) ]^2 + [z (t_{i+1}) - z (t_i) ]^2}, \] where \({\bf c} (t) = ( x (t), y (t),z (t))\). Applying the mean-value theorem to \(x (t), y (t)\), and \(z (t)\) on \([t_i, t_{i+1}]\), we obtain three points \(t_i^*, t^{**}_i,\) and \(t_i^{***}\) such that \begin{eqnarray*} x(t_{i+1}) - x (t_i) = x' ( t_i^*) ( t_{i+1} - t_i), \\[3pt] y ( t_{i+1}) - y (t_i) = y' ( t_i^{**}) ( t_{i+1} - t_i) , \end{eqnarray*}
and \[ z (t_{i+1}) -z (t_i)= z' (t_i^{***}) (t_{i+1} -t_i). \]
Thus, the line segment from \({\bf c}(t_i)\) to \({\bf c}(t_{i+1})\) has length \[ \sqrt{[x'(t_i^*) ]^2 + [y' (t_i^{**})]^2+ [z' ( t_i^{***}) ]^2} ( t_{i+1} - t_i). \]
Therefore, the length of our approximating polygonal line is \[ S_N = \sum_{i=0}^{N-1} \sqrt{[x'(t_i^*) ]^2 + [y' (t_i^{**})]^2+ [z' ( t_i^{***}) ]^2} ( t_{i+1} - t_i). \]
As \(N \to \infty\), this polygonal line approximates the image of \({\bf c}\) more closely. Therefore, we define the arc length of \({\bf c}\) as the limit, if it exists, of the sequence \(S_N\) as \(N \to \infty\). Because the derivatives \(x', y'\), and \(z'\) are all assumed to be continuous on \([a,b]\), we can conclude that, in fact, the limit does exist and is given by \[ {\mathop {\rm limit}_{N \to \infty}} S_N = \int_a^b \sqrt{[x'(t) ]^2 + [y' (t)]^2+ [z' (t)]^2}\, {\it dt}. \]
(The theory of integration relates the integral to sums by the formula \[ \int_a^b f (t) \,{\it dt} = {\mathop {\rm limit}_{N \to \infty}} \sum_{i=0}^{N-1} f (t_i^*) ( t_{i+1} - t_i), \] where \(t_0, \ldots , t_N\) is a partition of \([a,b], t_i^* \in [t_i,t_{i+1}]\) is arbitrary, and \(f\) is a continuous function. Here we have possibly different points \(t_i^*, t_i^{**}\), and \(t_i^{***}\), and so this formula must be extended slightly.)
Arc Length
The length of the path \({\bf c}(t)=(x(t),y(t),z(t))\) for \(t_0\leq t\leq t_1\), is \[ L({\bf c})=\int^{t_1}_{t_0}\sqrt{[x'(t)]^2+[y'(t)]^2+[z'(t)]^2}\,{\it dt}. \]
If \({\bf c}(t)\) represents the position of a particle at time \(t\), then \(L({\bf c})\) above represents "the total distance traveled" by the particle between \(t=t_0\) and \(t=t_1\).
example 1
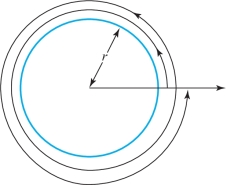
The arc length of the path \({\bf c}(t)=(r\,\cos t,r \,\sin t)\), for \(t\) lying in the interval \([0, 2\pi]\); that is, for \(0\leq t\leq 2\pi\), is \[ L({\bf c})=\int^{2\pi}_0\sqrt{(-r\,\sin t)^2+(r\,\cos t)^2}\, {\it dt}=2\pi r, \] which is the circumference of a circle of radius \(r\). If we had allowed \(0\leq t\leq 4\pi\), we would have obtained \(4\pi r\), because the path traverses the same circle twice (Figure 12.20).
229
For planar curves, we omit the \(z'(t)\) term, as in Example 1.
example 2
Consider the point with position function \[ {\bf c}(t)=(t-\,\sin t,1-\,\cos t), \] which traces out the cycloid discussed in Section 12.4 (see Figure 2.4.6). Find the velocity, the speed, and the length of one arch.
solution The velocity vector is \({\bf c}'(t)=(1-\,\cos t,\,\sin t)\), so the speed of the point \({\bf c}(t)\) is \[ \|{\bf c}'(t)\|={\sqrt{(1-\,\cos t)^2+\,\sin^2t}}=\sqrt{2-2\,\cos t}. \]
Hence, \({\bf c}(t)\) moves at variable speed although the circle rolls at constant speed. Furthermore, the speed of \({\bf c}(t)\) is zero when \(t\) is an integral multiple of \(2\pi\). At these values of \(t\), the \(y\) coordinate of the point \({\bf c}(t)\) is zero, and so the point lies on the \(x\) axis. The arc length of one cycle is \begin{eqnarray*} L({\bf c}) &=& \int^{2\pi}_0\sqrt{2-2\,\cos t}\,{\it dt}=2\int^{2\pi}_0\sqrt{\frac{1-\,\cos t}{2}}\,{\it dt}\\[6pt] &=& 2\int^{2\pi}_0\,\sin \frac{t}{2}\,{\it dt}\,\bigg(\hbox{because } 1-\,\cos t=2\,\sin^2 \frac{t}{2} \hbox{ and }\sin \frac{t}{2}\geq 0 \hbox{ on } [0,2\pi]\bigg)\\[6pt] &=& 4\bigg(-\cos \frac{t}{2}\bigg)\bigg|^{2\pi}_{0}=8.\\[-27pt] \end{eqnarray*}
If a path \({\bf c}(t)\) is differentiable on a closed interval and its derivative \({\bf c}'(t)\) is continous on that interval, we say that \({\bf c}(t)\) is \(C^1\). If a curve is made up of a finite number of pieces, each of which is \(C^1\) (with bounded derivative), we compute the arc length by adding the lengths of the component pieces. Such curves are called piecewise \(C^1\). Sometimes we just say “piecewise smooth.”
example 3
A billiard ball on a pool table follows the path \({\bf c}\colon\, [-1,1]\rightarrow {\mathbb R}^2\), defined by \({\bf c}(t)=(x(t),y(t))= (|t|, |t-\frac{1}{2}|)\). Find the distance traveled by the ball.
solution This path is not smooth, because \(x(t)=|t|\) is not differentiable at 0, nor is \(y(t)= |t-\frac{1}{2} |\) differentiable at \(\frac{1}{2}\). However, if we divide the interval \([-1,1]\) into the pieces \([-1,0],[0,\frac{1}{2}]\), and \([\frac{1}{2},1 ]\), we see that \(x(t)\) and \(y(t)\) have continuous derivatives on each of the intervals \([-1,0], [0,\frac{1}{2} ]\), and \([\frac{1}{2},1]\). (See Figure 12.21.)
230
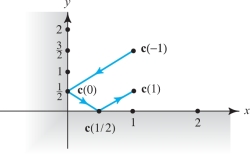
On \([-1,0],x(t)=-t,y(t)=-t+\frac{1}{2}\), so \(\|{\bf c}'(t)\|=\sqrt{2}\). Hence, the arc length of \({\bf c}\) between \(-1\) and 0 is \(\int^0_{-1}\sqrt{2}\,{\it dt}=\sqrt{2}\). Similarly, on \( [0,\frac{1}{2} ],x(t)=t, y(t)=-t+\frac{1}{2}\), and again \(\|{\bf c}'(t)\|=\sqrt{2}\), so that the arc length of \({\bf c}\) between 0 and \(\frac{1}{2}\) is \(\frac{1}{2}\sqrt{2}\). Finally, on \([\frac{1}{2},1]\) we have \(x(t)=t,y(t)=t-\frac{1}{2},\) and the arc length of \({\bf c}\) between \(\frac{1}{2}\) and 1 is \(\frac{1}{2}\sqrt{2}\). Thus, the total arc length of \({\bf c}\) is \(2\sqrt{2}\). Of course, we can also compute the answer as the sum of the distances from \({\bf c}(-1)\, {\rm to}\, {\bf c}(0) \,{\rm to}\, {\bf c}(\frac{1}{2})\) to \({\bf c}(1)\).
Here is an example in \({\mathbb R}^3\).
example 4
Find the arc length of \((\cos t,\,\sin t, t^2),0\leq t\leq \pi\).
solution The path \({\bf c}(t)=(\cos t,\,\sin t,t^2)\) has the velocity vector given by \({\bf v}=({-}{\sin t}, \,\cos t,2t)\). Because \[ \|{\bf v}\|=\sqrt{\,\sin^2 t+\,\cos^2 t+4t^2}=\sqrt{1+4t^2}=2\sqrt{t^2+\Big( \frac{1}{2}\Big)^2}, \] the arc length is \[ L({\bf c})=\int^\pi_02\sqrt{t^2+\bigg(\frac{1}{2}\bigg)^2}\,{\it dt}. \]
This integral may be evaluated using the following formula from the table of integrals: \[ \int \sqrt{x^2+a^2}{\,d} x=\frac{1}{2} \big[ x\sqrt{x^2+a^2}+a^2\,\log\, (x+\sqrt{x^2+a^2}) \big]+C. \]
Thus, \begin{eqnarray*} L({\bf c}) &=& 2\,{\bf \cdot}\, \frac{1}{2}\left[ t\sqrt{t^2+\bigg(\frac{1}{2}\bigg)^2}+ \bigg(\frac{1}{2}\bigg)^2 \log\left(t+\sqrt{t^2+\bigg(\frac{1}{2}\bigg)^2}\right)\right] \Bigg|^\pi_{t=0}\\[4pt] &=&\pi\sqrt{\pi^2+\frac{1}{4}}+\frac{1}{4}\log \bigg(\pi+\sqrt{\pi^2+\frac{1}{4}}\bigg)-\frac{1}{4} \log\bigg(\sqrt{\frac{1}{4}}\bigg)\\[4pt] &=&\frac{\pi}{2}\sqrt{1+4\pi^2}+\frac{1}{4}\log\, (2\pi+ \sqrt{1+4\pi^2})\approx10.63. \\[-16pt] \end{eqnarray*}
As a check on our answer, we may note that the path \({\bf c}\) connects the points (1, 0, 0) and \((-1,0,\pi^2)\). The distance between these points is \(\sqrt{4+\pi^2}\approx 3.72\), which is less than 10.63, as it should be.
Question 12.30 Section 12.3 Progress Check Question 1
Find the arc length of the part of the helix \({\bf c}(t)= (\cos t, \sin t, t)\) where \(0 \leq t \leq 2 \pi\).
| A. |
| B. |
| C. |
| D. |
| E. |
The Differential of Arc Length
The arc-length formula suggests that we introduce the following notation, which will be useful in our discussion of line integrals.
231
Arc-Length Differential
An infinitesimal displacement of a particle following a path \({\bf c}(t)=x(t){\bf i}+y(t){\bf j}+z(t){\bf k}\,\) is \[ d{\bf s}={\it dx}\, {\bf i}+{\it dy}\, {\bf j}+{\it dz}\, {\bf k}=\bigg(\frac{{\it dx}}{{\it dt}}{\bf i}+\frac{{\it dy}}{{\it dt}}{\bf j}+\frac{{\it dz}}{{\it dt}}{\bf k}\bigg)\,{\it dt}, \] and its length \[ ds={\textstyle\sqrt{{\it dx}^2+{\it dy}^2+{\it dz}^2}}=\sqrt{\bigg(\frac{{\it dx}}{{\it dt}}\bigg)^2+ \bigg(\frac{{\it dy}}{{\it dt}}\bigg)^2+\bigg(\frac{{\it dz}}{{\it dt}}\bigg)^2}\,{\it dt} \] is the differential of arc length. See Figure 12.22.
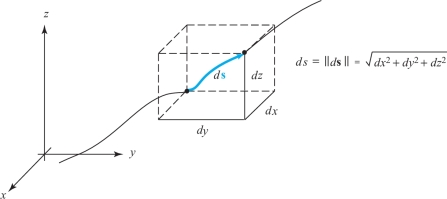
These formulas help us remember the arc-length formula as \[ \hbox{arc length}=\int^{t_1}_{t_0}{\,d} s. \]
As we have done before with such geometric concepts as length and angle, we can extend the notion of arc length to paths in \(n\)-dimensional space.
Arc Length in \({\mathbb R}^n\)
Let \({\bf c}\colon\, [t_0,t_1]\rightarrow {\mathbb R}^n\) be a piecewise \(C^1\) path. Its length is defined to be \[ L({\bf c})=\int^{t_1}_{t_0}\|{\bf c}'(t)\|\,{\it dt}. \]
The integrand is the square root of the sum of the squares of the coordinate functions of \({\bf c}'(t)\): If \[ {\bf c}(t)=(x_1(t),x_2(t),\ldots,x_n(t)), \] then \[ L({\bf c})=\int^{t_1}_{t_0}{\sqrt{(x_1'(t))^2+(x_2'(t))^2 +\cdots +(x_n'(t))^2}}\,{\it dt}. \]
232
example 5
Find the length of the path \({\bf c}(t)=(\,\cos t,\,\sin t,\,\cos 2t,\sin 2t)\) in \({\mathbb R}^4\), defined on the interval from 0 to \(\pi\).
solution We have \({\bf c}'(t)=({-}{\sin t},\,\cos t,-2\,\sin 2t,2\,\cos 2t)\), and so \[ \|{\bf c}'(t)\|={\sqrt{\,\sin^2 t+\,\cos^2 t+4\,\sin^2 2t +4\,\cos^2 2t}}={\sqrt{1+4}}={\textstyle\sqrt{5}}, \] a constant, so the length of the path is \[ \int^\pi_0\sqrt{5}\,{\it dt}=\sqrt{5}\pi. \]
It is common to introduce the arc-length function \(s (t)\) associated to a path \({\bf c}(t)\) given by \[ s (t) = \int_a^t \| {\bf c}' ( u) \|\, d u, \] so that (by the fundamental theorem of calculus) \[ s' (t)= \| {\bf c}' (t) \| \] and \[ \int_a^b s' (t)\, {\it dt} = s (b) - s( a) = s(b). \]
example 6
Consider the graph of a function of one variable \(y=f(x)\) for \(x\) in the interval [\(a, b\)]. We can consider it to be a curve parametrized by \(t = x\), namely, \({\bf c}(x)=(x, f(x))\) for \(x\) ranging from \(a\) to \(b\). The arc-length formula gives \[ L({\bf c})=\int^b_a \sqrt{1+[f'(x)]^2} \, {\it dx}, \] which agrees with the formula for the length of a graph from one-variable calculus.