exercises
234
Find the arc length of the given curve on the specified interval in Exercises 1 to 6.footnote #
Question 12.31
\((2\,\cos t,2\,\sin t,t)\), for \(0\leq t\leq 2\pi\)
Question 12.32
\((1,3t^2,t^3)\), for \(0\leq t\leq 1\)
Question 12.33
\((\sin 3t,\,\cos 3t,2t^{3/2})\), for \(0\leq t\leq 1\)
Question 12.34
\(\left(t+1,{\displaystyle\frac{2\sqrt{2}}{3}}t^{3/2}+7,{\displaystyle\frac{1}{2}}t^2 \right)\), for \(1\leq t\leq 2\)
Question 12.35
\((t,t,t^2)\), for \(1\leq t\leq 2\)
Question 12.36
\((t,t\,\sin t,t\,\cos t)\), for \(0\leq t\leq \pi\)
Question 12.37
Find the arc length of \(\textbf{c}(t)=(t, |t|)\) for \(-1 \leq t\leq 1\).
Question 12.38
Recall from Section 12.4 that a rolling circle of radius \(R\) traces out a cycloid, which can be parametrized by \(\textbf{c}(t)= (Rt-R\sin t, R- R\cos t)\). One arch of the cycloid is completed from \(t=0\) to \(t= 2\pi\). Show that the length of this arch is always 4 times the diameter of the rolling circle.
Question 12.39
Let \(C\) be the line segment connecting the point \(\textbf{p} =(1, 2, 0)\) to the point \(\textbf{q}=(0, 1, -1)\).
- (a) Find a curve \(\textbf{c}(t) \colon [a, b] \to \mathbb R^3\) that traces out \(C\).
- (b) Find the arc length of \(\textbf{c}(t)\).
- (c) Find \(|| \textbf{p}-\textbf{q} ||\).
Question 12.40
Compute the length of the curve \(\textbf{c}(t)=(\log(\sqrt{t}), \sqrt{3}t, \frac{3}{2}t^2)\) for \(1 \leq t \leq 2\).
Question 12.41
Find the length of the path \({\bf c}(t)\), defined by \({\bf c}(t)=(2\,\cos t,2\,\sin t,t)\), if \(0\leq t\leq 2\pi\) and \({\bf c}(t)=(2,t-2\pi,t)\), if \(2\pi\leq t \leq 4\pi\).
Question 12.42
Let \({\bf c}\) be the path \({\bf c} (t)=(t,t \,\sin t, t \,\cos t)\). Find the arc length of \({\bf c}\) between the two points \((0, 0, 0)\) and \((\pi,0,-\pi)\).
Question 12.43
Let \({\bf c}\) be the path \({\bf c} (t) = (2t, t^2 , \log t)\), defined for \(t > 0\). Find the arc length of \({\bf c}\) between the points \((2, 1, 0)\) and \((4, 4, \log 2)\).
Question 12.44
The arc-length function \(s (t)\) for a given path \({\bf c} (t)\), defined by \(s (t) = \int_a^t \| {\bf c} ' (\tau) \| \,d \tau\), represents the distance a particle traversing the trajectory of \({\bf c}\) will have traveled by time \(t\) if it starts out at time \(a\); that is, it gives the length of \({\bf c}\) between \({\bf c} (a)\) and \({\bf c} (t)\). Find the arc-length functions for the curves \({\alpha} (t) = (\cosh t, \,\sinh t,t)\) and \({\beta} (t) = (\cos t , \,\sin t,t)\), with \(a=0.\)
Question 12.45
Let \({\bf c} (t)\) be a given path, \(a \le t \le b\). Let \(s=\alpha (t)\) be a new variable, where \(\alpha\) is a strictly increasing \(C^1\) function given on \([a,b]\). For each \(s\) in \([\,\alpha (a), \,\alpha (b)]\) there is a unique \(t\) with \(\,\alpha (t) =s\). Define the function \({\bf d}\colon [ \,\alpha (a), \,\alpha (b)] \to {\mathbb R}^3\) by \({\bf d} (s)={\bf c} (t)\).
- (a) Argue that the image curves of \({\bf c}\) and \({\bf d}\) are the same.
- (b) Show that \({\bf c}\) and \({\bf d}\) have the same arc length.
(c) Let \(s = \,\alpha (t) = \int_a^t \|{\bf c}' (\tau) \|\, d \tau\). Define \({\bf d}\) as above by \({\bf d} (s) = {\bf c} (t)\). Show that \[ \Big\|\frac{d}{ds} {\bf d} (s)\Big\|=1. \]
The path \(s \mapsto {\bf d} (s)\) is said to be an arc-length reparametrization of \({\bf c}\) (see also Exercise 17).
235
Exercises 16, 17, and 20–23 develop some of the classic differential geometry of curves.
Question 12.46
Let \({\bf c} \colon\, [a,b] \to {\mathbb R}^3\) be an infinitely differentiable path (derivatives of all orders exist). Assume \({\bf c}' (t) \ne {\bf 0}\) for any \(t\). The vector \({\bf c}' (t) / \| {\bf c}' (t) \| = {\bf T} (t)\) is tangent to \({\bf c}\) at \({\bf c} (t)\), and, because \(\|{\bf T} (t) \| =1, {\bf T}\) is called the unit tangent to \({\bf c}\).
- (a) Show that \({\bf T}' (t)\, {\cdot}\, {\bf T} (t) =0.\) [HINT: Differentiate \({\bf T} (t)\, {\cdot}\, {\bf T} (t) =1.\)]
- (b) Write down a formula for \({\bf T}' (t)\) in terms of \({\bf c}\).
Question 12.47
- (a) A path \({\bf c} (s)\) is said to be parametrized by arc length or, what is the same thing, to have unit speed if \(\|{\bf c}' (s)\|=1\). For a path parametrized by arc length on \([a,b]\), show that \(l ( {\bf c}) =b-a\).
- (b) The curvature at a point \({\bf c} (s)\) on a path is defined by \(k = \| {\bf T}' (s) \|\) when the path is parametrized by arc length. Show that \(k = \| {\bf c}'' (s) \|\).
- (c) If \({\bf c}\) is given in terms of some other parameter \(t\) and \({\bf c}' (t)\) is never \({\bf 0}\), show that \(k = \| {\bf c} ' (t) \times {\bf c}'' (t) \| / \| {\bf c} ' (t) \|^3\).
- (d) Calculate the curvature of the helix \({\bf c} (t) = (1 / \sqrt{2}) (\cos t, \,\sin t,t)\). (This \({\bf c}\) is a scalar multiple of the right-circular helix.)
Question 12.48
Show that any line \({\bf l}(t)=\textbf{x}_0+t\textbf{v}\), where \(\textbf{v}\) is a unit vector, has zero curvature.
Question 12.49
Consider the parametrization of the unit circle given by \(\textbf{c}(t)=(\cos t, \sin t)\).
- (a) Verify that \(\textbf{c}\) is parametrized by arc length.
- (b) Show that the curvature \(k\) of \(\textbf{c}\) is constant.
Question 12.50
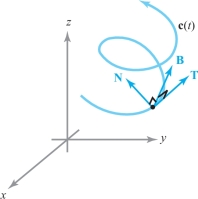
If \({\bf T}' (t) \ne {\bf 0}\), it follows from Exercise 16 that \({\bf N} (t) = {\bf T}' (t) / \|{\bf T}' (t) \|\) is normal (i.e., perpendicular) to \({\bf T} (t); {\bf N}\) is called the principal normal vector. Let a third unit vector that is perpendicular to both \({\bf T}\) and \({\bf N}\) be defined by \({\bf B} = {\bf T} \times {\bf N}; {\bf B}\) is called the binormal vector. Together, \({\bf T}, {\bf N},\) and \({\bf B}\) form a right-handed system of mutually orthogonal vectors that may be thought of as moving along the path (Figure 12.12). Show that
- (a) \(\displaystyle \frac{d {\bf B}}{{\it dt}} \ {\cdot}\ {\bf B} =0.\)
- (b) \(\displaystyle \frac{d {\bf B}}{{\it dt}}\ {\cdot}\ {\bf T} =0\).
- (c) \(d {\bf B} / {\it dt}\) is a scalar multiple of \({\bf N}\).
Question 12.51
If \({\bf c} (s)\) is parametrized by arc length, we use the result of Exercise 20(c) to define a scalar-valued function \(\tau\), called the torsion, by \[ \frac{d {\bf B}}{ds} = - \tau {\bf N}. \]
- (a) Show that \(\tau = [ {\bf c} ' (s) \times {\bf c}'' (s) ]\,{\cdot}\, {\bf c}''' (s) / \| {\bf c}'' (s) \|^2\).
- (b) Show that if \({\bf c}\) is given in terms of some other parameter \(t\), \[ \tau= \frac{[{\bf c}' (t) \times {\bf c}'' (t) ]\,{\cdot}\, {\bf c}''' (t)}{\| {\bf c}' (t) \times {\bf c}'' (t) \|^2}. \] Compare with Exercise 17(c).
- (c) Compute the torsion of the helix \({\bf c} (t) = (1/ \sqrt{2})(\cos t, \sin t,t)\).
Question 12.52
Show that if a path lies in a plane, then the torsion is zero. Do this by demonstrating that \({\bf B}\) is constant and is a normal vector to the plane in which \({\bf c}\) lies. (If the torsion is not zero, it gives a measure of how fast the curve is twisting out of the plane of \({\bf T}\) and \({\bf N}\).)
Question 12.53
- (a) Use the results of Exercises 17, 20, and 21 to prove the following Frenet formulas for a unit-speed curve: \[ \frac{d {\bf T}}{ds} = k {\bf N}; \quad \frac{d {\bf N}}{ds} = - k {\bf T} + \tau {\bf B}; \quad \frac{d {\bf B}}{ds} = - \tau {\bf N}. \]
- (b) Reexpress the results of part (a) as \[ \frac{d}{ds} \Bigg(\begin{array}{c} {\bf T} \\ {\bf N} \\ {\bf B} \end{array} \Bigg) = {\omega} \times \Bigg(\begin{array}{c} {\bf T} \\ {\bf N} \\ {\bf B} \end{array} \Bigg) \] for a suitable vector \({\omega}\).
Question 12.54
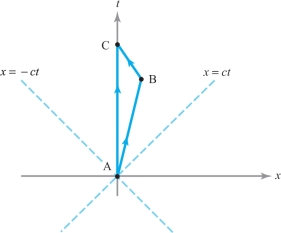
In special relativity, the proper time of a path \({\bf c} \colon [a,b] \to {\mathbb R}^4 \) with components given by \({\bf c} ( \lambda) = ( x (\lambda), y (\lambda),\) \(z (\lambda), t (\lambda))\) is defined to be the quantity \[ \int_a^b \sqrt{-[x' (\lambda)]^2 - [ y' (\lambda)]^2 - [ z' (\lambda)]^2 + c^2 [t' (\lambda)]^2} \, d \lambda, \] where \(c\) is the velocity of light, a constant. In Figure 12.24, show that, using self-explanatory notation, the “twin paradox inequality” holds: \[ \hbox{proper time (AB) + proper time (BC) < proper time (AC)}. \]
236
Question 12.55
The early Greeks knew that a straight line was the shortest possible path between two points. Euclid, in his book Optics, stated the “principle of the reflection of light”—that is, light traveling in a plane travels in a straight line, and when it is reflected across a mirror, the angle of incidence equals the angle of reflection.
The Greeks could not have had a proof that straight lines provided the shortest path between two points because they, in the first place, had no definition of the length of a path. They saw this property of straight lines as more or less “obvious.”
Using the justification of arc length in this section and the triangle inequality of Section 11.5, argue that if \({\bf c}_{0}\) is the straight-line path \(c_{0}(t)=t {\rm P} + (1 - t)\)Q between P and Q in \({\mathbb R}^{3}\), then \[ L({\bf c}_{0}) \le L({\bf c}) \] for any other path \({\bf c}\) joining P and Q.